Stanford CS143 Compiler Fall2014 个人笔记

introduction

1. Deference between Compilers with Interpreters
   Compiler is off-line, and it’s imput is “program” then compiler it to exec witch can coculate Data to Output.
   Interpreters is on-line, and it’s input is Program and Data, it interpreter the Program line by line, and excute the code.
2. History
   1954 IBM develops the 704. In this time, software is more expensive than hardware.
3. Speedcoding
   1954 John Backus.today’s interperters. very slow.
   than he invented Fortran1(1954-1957). It’s the first compiler.
   （好吧，英语记笔记有点慢）并且编译的核心由此确定为“理论(Theory)+练习(Pratice)”
4. 编译原理分为：lexical analysis, parsing, sematic analysis, optimization, code generation
   lexical analysis和parsing注重句法分析，sematic注重语义，

1.1 编译器的结构

人类是如何理解一段英语的

理解语句	对应编译过程
This is a sentence.	if x == y then z = 1; else z = 2;
理解单词 将句子分割成单词集 {‘This’, ‘is’, ‘a’, ‘sentence’}	词法分析 将独立的程序文本分割成单词或tokens（标记） 可以识别出关键字{‘if’, ‘and’, ‘else’}、变量名{‘x’, ‘y’, ‘z’}、常量{‘1’, ‘2’}、操作符{’==’, ‘’=’, ‘=’}
理解句子结构	语法分析（语法树）
理解句子意思 这是会有歧义的	语义分析 强制规定，避免模糊语言
简化语言表示	自动代码优化 但当Y==NaN时不能这么做
翻译成其他语言	code生成

1.2 经济型程序语言
问1：为什么有这么多程序语言？
如，科学计算→Fortran，商业程序→SQL，系统程序→C/C++
答：不同程序所解决的领域（application domains）是不同的

问2：为什么有新的程序语言出现？
答：对编程语言来说，需要投入的前期编程教育占据了支出的主要部分。
且现在主流语言之间的差距并不大。
创建一个新编程语言很容易。当新语言带来的生产力大于培训成本时，选择创建新语言。
编程语言尝试填补空缺

问3：好的程序语言是什么？

3. 词法分析Lexical Analysis

3.1 词法分析的目的

将源码分解为对和词汇表

3.1.1 名词释义

名词	词义
Identifier	字符串或由字符开始的数字串
Integer	非空数字组成的字符串
Keyword	“else” or “if” or “begin” or …
Witespace	非空字符串，这个字符串由空格、换行符、制表符构成
Operator	运算符

3.1.2 词法分析概要

1. 将源码的字串归类成Tocken class
2. 通过Tocken与语法分析沟通

3.1.3 词素例子

3.2 词法分析例子

3.2.1 FORTRAN

FORTRAN规则：空格是无影响的（“var1” == “va r1”）
向前看规则
这说明了词法分析的任务：

1. 分割文本。从左向右读源程序，生成Tocken，一次个状态识别一个Tocken
2. “向前看”用来解决一个Tocken的终止和另一个Tocken的开始

3.2.2 PL/1

（PL/1是一个IBM设计的编程语言）

特点：

1. 关键字不保留
   
2. DECLARE二义性
   

3.2.3 C++

在<>和>>、<<之间的问题
如：Foo ，这里出现了>>，会和流>>混淆。所以需要将这里的>>改成> >(加了个空格)

3.3 正规语言

Lexical structure = token classes

3.3.1 正规表达式

3.3.1.1 正规表达式Regular Expressions

正规表达式由{单个字符，空字符}构成
　空字符用"$\epsilon$"表示

3.3.1.2 正规表达式的操作

操作名	方法示意
Union
Concatenation
Iteration

定义：$\Sigma$ 是一个正规表达式中各正规式的组成元素集合

上图中，都是在给定的$\Sigma$(即正规表达式构成元素)组成的语法$R$(grammer)
举例说明：

3.3.2 正规语言Formal Languages

定义：设$\Sigma$是一个字符集。一个在$\Sigma$上产生的语法是，从$\Sigma$上产生的字符串集。（主要部分：语法是字符串集，其他定语自己看懂）
就像英文字母表是英语字符构成的，而英文语言是由英文句子构成的
Alphabet = ASCII
Language = C programs

3.3.2.? Meaning Function L

Meaning Function L将语法（Syntax）映射到语义（Semantics）上去

（上图exp为expression缩写）
使用Meaning Function的意义：

1. 分清语法和语义
2. 有利于将符号（notation）看做成一个独立的问题
3. 表达式和语义并不是一一对应的

上图展示了，不同语法通过Meaning Function可能映射到相同语义上去。这有助于我们将相同功能、不同语法写成的程序，用高效的程序代替低效的程序。
并且，语法不会映射到多个语义上去。（无二义性）

3.3.3 正规表达式如何说明编程语言中的不同方向

注：$A^{+}=A{A}^{\ast }=\bigcup _{i>0}A$

要描述的类型	描述方法
Keyword	‘if’+‘else’+then’…
Interger	digit = ‘0’+‘1’+…+‘9’ $digi{t}^{\ast }$
Identifier	letter=[a-zA-Z] ([a-z](a到z求并)) $letter(letter+digit{)}^{\ast }$
Whitespace	’ ‘+’\n’+’\t’

例子：识别email地址的正规表达式
[email protected]
正规式表达：$letter{+}^{\prime }{@}^{\prime }|letter{+}^{\prime }{.}^{\prime }+letter{+}^{\prime }{.}^{\prime }+letter$

PASCAL语言中的正规表达式例子：

（这里的+表示连接，在往上的文章中有用(1+0)这样表示的正规式中的+表示或，因为课件中用的是+表示或，十分有歧义，并且龙书中用的也是|。下面我尽量使用|，用以区分+，请注意）如下图所示。。。这老师用的跟我校用的那本清华的编译原理讲的也不一样，真讨厌

3.4 词法规范（lexical specification）

词法检测过程：

1. 根据词素写出Tocken类
   
2. 构建一个符合所有词素和Token的R
   
3. 输入
   
4. 
   
5. 
   

CTMD垃圾CSDN，Ctrl+S不能保存，写了1000多字全没了。。。。Scheiße！

4 语法分析

4.1 上下文无关文法

4.1.1 结构

左优先和右优先
规范推导为右优先

4.1.2 二义文法

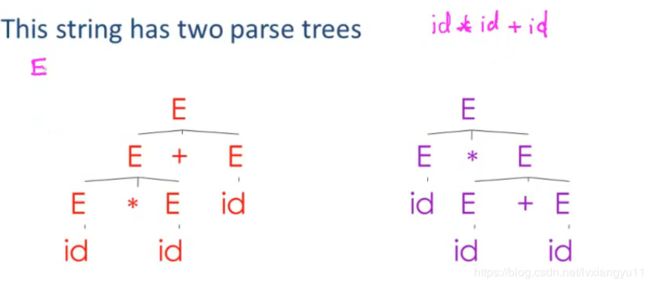
解决方法：将二义文法改写成非二义文法

改写成：（消除左递归）

注意：

4.2 处理问题

4.2.1 问题的种类

4.2.2 处理问题需要做的事

1. 准确且清晰地报告错误
2. 快速地从错误中恢复过来（状态）

4.2.3 处理问题的方法

4.2.3.1 恐慌模式Panic mode

处理方式：一直接着吃，直到找到了一个正确的role
寻找同步token
z.B.


可以使用一个特殊的终结符"error"来描述有多少输入需要略过

4.2.3.2 错误产生式 Error Productions

只能知道语法中简单的错误
z.B.

4.2.3.3 自动的局部或全局矫正 Automatic local or global correction

现在并不常用这种

4.2.3.4 过去和现在比较

4.3 语法树

编译器剩下一部分需要一个能代替程序的结构。
抽象语法树：近似语法树但忽略一些细节、简单地描述成AST（Abstract Syntax Tree）

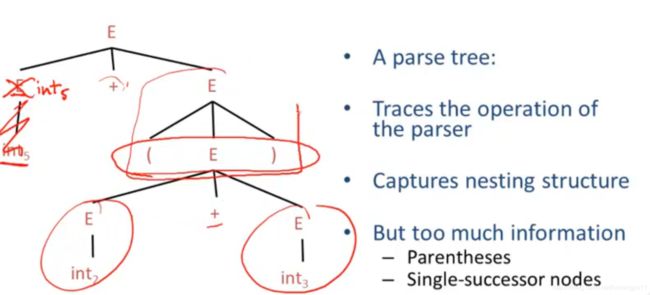
改写成这样

4.4递归下降的语法分析（自顶向下的语法分析）

语法树构建方法：自顶向下，从左到右
先序遍历地生成Terminals
z.B.

生成过程，注意有回归






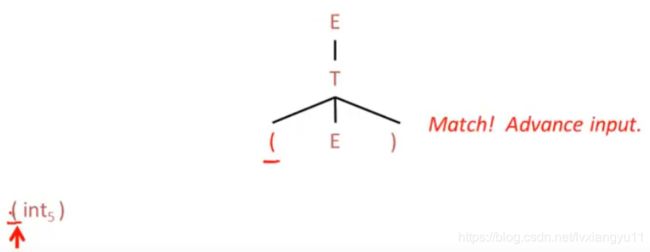
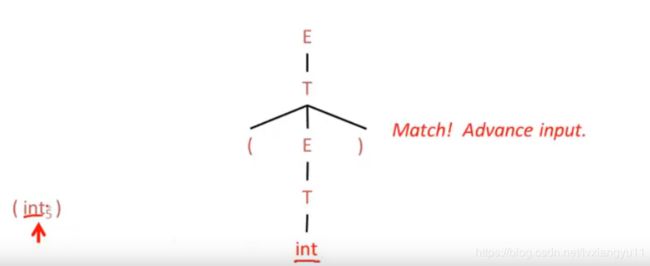
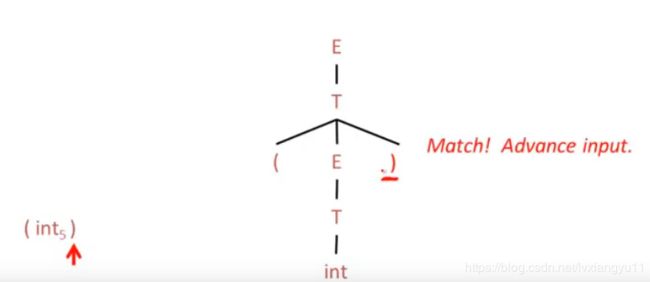
accept

4.4.2 举一个RD algorithm例子

对于语法E：{
E → T | T+E
T → int | int*T | (E)
}
Token有：INT, OPEN, CLOSE, PLUS, TIMES
global next指向下一输入的token

1. 定义一个返回值是bool值的检测函数，它检测将要输入的token是不是一个token。

// 返回当前token是否符合选择的token，并将指针移到下一个输入上去
bool term(Token tok){
	return *next++==tok;
}

定义一系列的代表产生式的函数S " bool Sn() { … } "，只有在相同时才返回为真。
定义一个包含所有产生式的函数S " bool S() { … } "

// z.B. 对于产生式 "E→T"有函数
bool E1() { return T(); }
// z.B. 2: "E→T+E":
bool E2() { return T() && term(PLUS) && E(); }
bool E(){
	Token *save = next; // 在尝试任何匹配前，先把**接下来**要从哪去token的位置记录下来。
	return (next = save, E1()) 
		|| (next = save, E2());
}

2. 定义接下来的T的函数

// 对于 T→int
bool T1() { return term(INT); }
// 对于 T→int * T
bool T2() { return term(INT) && term(TIMES) && T(); }
// 对于 T→(E)
bool T3() { return term(OPEN) && E() && term(CLOSE); }

// T → int | int*T | (E)
bool T(){
	TOKEN *save = next;
	return (next = save, T1()) || (next = save, T2()) || (next = save, T3()); 
}

3. 开始语法分析
   初始化next指向输入字符串的第一个字符，调用函数E()

问题： 这对于输入"int * int "会reject，因为第一次使用的是E→int进行推导，如果使用E→int*T就不会出错。所以有问题”如果一个产生非终结符的产生式被使用了，则不再有回溯回来检测此时使用别的产生式的可能“
通常上，自顶向下递归分析需要支持全回溯，才可以进行完整的语法检测。
虽然正常情况下不使用这种算法，但这算法容易手工实现。在一个非终结符只能推导出一个终结符情况下是可用的。消除例子中的公共前缀left factoring就可以用了:)。

4.4.3 消除左递归（left recursion）

举个例子：

// S → Sa
bool S1() { return S() && term(a); }
bool S() {return S1();}

这里的S会产生无穷的递归。一个左递归语法要求没有这样的S，这样的非终结符S使得S可以加步推导出S$\alpha$
考虑这样的语法：
$S\to S\alpha |\beta$
它会产生这样的语言：
这导致最后生成了$\beta$，它从右向左依次生成，因此可以右递归地生成。
上式也可写成右递归式：(从左向右生成)

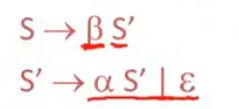
更多的消除左递归式的例子：