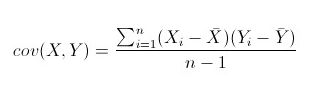numpy中的cov(方差计算)简单介绍

协方差矩阵的计算公式可以参考这一篇博文

协方差矩阵

官方文档介绍

简单使用介绍

有下面一个例子，计算数组[1,2,3]和[1,1,1]的协方差矩阵

import numpy as np

X = np.array([1,2,3])
Y = np.array([1,1,1])
A = np.stack((X, Y), axis=0)
print("source:\n", A)
print("cov:\n", np.cov(A))

结果如下：

也可以根据公式自己实现这一函数

import numpy as np

X = np.array([1,2,3])
Y = np.array([1,1,1])
A = np.stack((X, Y), axis=0)

dim1 = np.mean(X)
dim2 = np.mean(Y)
cov11 = sum((X-dim1)*(X-dim1))/(A.shape[1]-1)
cov12 = sum((X-dim1)*(Y-dim2))/(A.shape[1]-1)
cov21 = sum((Y-dim2)*(X-dim1))/(A.shape[1]-1)
cov22 = sum((Y-dim2)*(Y-dim2))/(A.shape[1]-1)
cov = np.array([cov11, cov12, cov21, cov22]).reshape(2,2)
print(cov)

计算结果也是一致的

我们再来一个3维数组的例子

import numpy as np

X = np.array([1,2,3,4])
Y = np.array([3,2,7,9])
Z = np.array([-1,0,-1,1])
A = np.stack((X, Y, Z), axis=0)
print("source:\n", A)
print("cov:\n", np.cov(A))
print("===============")

dim1 = np.mean(X)
dim2 = np.mean(Y)
dim3 = np.mean(Z)
cov11 = sum((X-dim1)*(X-dim1))/(A.shape[1]-1)
cov12 = sum((X-dim1)*(Y-dim2))/(A.shape[1]-1)
cov13 = sum((X-dim1)*(Z-dim3))/(A.shape[1]-1)
cov21 = sum((Y-dim2)*(X-dim1))/(A.shape[1]-1)
cov22 = sum((Y-dim2)*(Y-dim2))/(A.shape[1]-1)
cov23 = sum((Y-dim2)*(Z-dim3))/(A.shape[1]-1)
cov31 = sum((Z-dim3)*(X-dim1))/(A.shape[1]-1)
cov32 = sum((Z-dim3)*(Y-dim2))/(A.shape[1]-1)
cov33 = sum((Z-dim3)*(Z-dim3))/(A.shape[1]-1)
cov = np.array([cov11, cov12, cov13, cov21, cov22, cov23, cov31, cov32, cov33]).reshape(3, 3)
print(cov)

结果如下

可以看出也是一致的。