KMP 算法 Java 代码讲解及 leetcode 对应题目

什么是 KMP 算法？

该算法因为其优秀的简称获得江湖称号 "看毛片算法"，简单来说 KMP 算法就是解决字符串匹配的一种算法，它通常用来解决主字符串和模式字符串的匹配问题，如存在字符串 A = "ababcde" 和 字符串 B = "abc"，那么可以延伸出如下几个问题：

1. 判断字符串 B 是否存在于字符串 A 中 （相当于实现 java 字符串的 contains() 方法）
2. 判断字符串 B 在字符串 A 中第一次出现的位置 （相当于实现 java 字符串的 indexOf() 方法）
3. 求出字符串 B 和字符串 A 连续最长重复字符串的个数 （如 "abde" 与 "abc" 最长连续重复字符串为 "ab", 长度为 2）

为什么需要 KMP 算法？

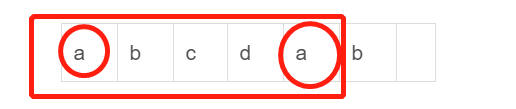
拿上面第一个问题举例，判断字符串 B = "abcabb" 是否存在于 A = "abcabcabb" 中；

常规的解题思路是暴力解法，首先从 A 的第一个字符为开始结点，然后判断从该节点开始，后面连续 B.length() 个字符，是否跟 B 中的字符是一样的，如果不是，那就从 A 的第二个字符为开始结点再往后查找，一直遍历到 A 的第 A.length() - B.length() 个
字符（因为再往后的话就没有 B 那么多字符了），代码如下：

for (int i = 0; i <= A.length() - B.length(); i++) {
    int b = 0;
    for (int a = i; b < B.length(); b++, a++) {
        if (A.charAt(a) != B.charAt(b)) {
            break;
        }
    }
    if (b == B.length()) {
        return true;
    }
}

可以看出来，上面算法的时间复杂度为 O(A.length()*B.length())。并不是很高效的算法。这也就引出了 KMP 算法

KMP 算法的原理

如图所示，当遍历到字符串 A 中的字符 c 和 字符串中最后一个字符 b 的时候，发生了不相等的情况，很可惜对不对，按照上面那种暴力的解法是要怎么做呢，就要从字符串 A 中的第 2 个字符 b 开始，字符串 B 的第一个字符 a 开始重新遍历，很生气对不对？明明已经都快成功了，结果你告诉我要重来，那能不气么，好，这个时候 KMP 就跳了出来语重心长地告诉你：不重来，你之前的努力没有白费！

那 KMP 是怎么是怎么做的呢？当我们发现 B 中最后一个字符 b 跟 A 中的 c 不一a致的时候，不是全部否定之前的努力推倒重来，而是直接转变为下一种状态，相当于字符串 A 中的 "ab" 和 B 中的 "ab" 已经比较过了，在此基础上继续比较：

往这个状态转换的原则就是，从字符串 A 的字符 c 开始往前，字符串 B 的从首字母往后（这两个都是从前往后的顺序，比如上面都是"ab"）,找到最长的相同的序列，那么拿到的这个序列相当于比较过，不需要再次进行比较，下次从后面的字符开始比较即可，（可以想想为什么可以这样，动动你的小脑瓜），然后你可能会问，刚刚说的那个过程不还是要遍历，也是需要时间的么，KMP做的就是再这个过程不需要再次遍历，用 O(1) 的时间就能拿得到结果，这就是 KMP 算法的原理了。

简单来说，KMP 算法就是兑现你曾经努力的一个算法，让你之前的积累能在以后用得上。是不是感觉有点像 DP ? 你懂我意思把？

KMP 算法的具体实现

相关概念介绍

在讲具体实现之前，先讲一个概念：最长公共前后缀，即前缀和后缀共同的长度，是不是一脸懵逼？所以说只看概念是不会懂的，这辈子都不可能懂的，懂我意思吧？所以还是看例子吧

比如：

字符串 "a" 的前缀和后缀都为空集， 故最长公共前后缀为空

字符串 "ab" 的前缀为 "a"，后缀为 "b"， 最长公共前后缀空

字符串 "aba" 的前缀为 "a" 和 "ab", 后缀为 "a" 和 "ba"，最长公共前后缀为 "a"

字符串 "abab" 的前缀为 "a", "ab" 和 "aba"， 后缀为 "b", "ab" 和 "bab", 最长公共前后缀为 "ab"

字符串 "aaa" 的前缀为 "a" 和 "aa"， 后缀为 "a" 和 "aa"，最长公共前后缀为 "aa"

好，我猜你现在应该懂了，那这公共前缀有什么用呢？让我们回到上面的图：

 

开始实操

上面怎么说的来着？上面分析的时候是这么说的："从字符串 A 的字符 c 开始往前，字符串 B 的从首字母往后（这两个都是从前往后的顺序，比如上面都是"ab"）,找到最长的相同的序列"，按照这句话的意思是找到了 X 区和 Z 区，找到 X 和 Z 之后，直接从这两个区的后面再进行比较，能省下不少事，那么怎么能快速找到 X 和 Z 呢？

首先我们此时已经遍历到字符串 A 中的 c 和字符串 B 中的 b, 那么说明 c 之前的序列和 b 之前的序列是完全相同的，即 X 和 Y 一定是相同的，那么问题从 X 找 Z 变成了从 Y 找 Z， 你那机灵的小眼睛（大眼睛）有没有发现什么？，这不就是最长公共前后缀吗？问题不久转化为了求下面字符串的公共前后缀么？所以现在我们就可以完全不再考虑主字符串 A, 把精力全放在模式串 B 上就好了，由此引出了另一个概念，就是 next[] 数组，next[i] 表示字符串下标 0 到下标 i-1  的最长公共前后缀的长度，以字符串 B 为例，当 Y 区域后面的字符 b 发生失配的时候，我们的关注点应该是其前面字符串 "abcab" 的最长公共前后缀，品，你细品，那这样的话，还是以上边字符串 B 为例，初始化 next[0] = -1 (当然因为其实next[0]就没有实际意义了，你让它等于什么都可以，只要你知道并能和其它的 next[i] 区别开来就好了),next[1] 对应 "a" 故 next[1] = 0, next[4] 对应 "abca"，故 next[4] =  1, 同理，next[5] 对应字符串 "abcab", 故 next[5] = 2, 另外，字符串 "aaaa" 的 next[] 数组值为 next[1] = 0, next[2] = 1, next[3] = 2。

跟着上面那个例子走一遍匹配流程吧：首先第一步求出模式串 B 的 next 数组，next[0] = -1, next[1] = 0, next[2] = 0, next[3] = 0，next[4] = 1, next[5] = 2。第二步就是匹配了，另 i = 0, j = 0, i 和 j 分别代表字符串 A 和字符串 B 当前匹配的位置，我们发现，当 i = 0, j = 0时，A 和 B 匹配， 然后就另 i = 1, j = 1， 发现也匹配，然后 i 和 j 继续增加，当 i = 5,j = 5 时，发现不匹配的情况出现，此时 i 不变，j = next[j], 因为 next[5] = 2, 故 j 被置为 2, 此时，i = 5, j = 2, 也就变成了下面这个状态：

然后发现此时匹配了，然后 i = 6,j = 3 发现也匹配，继续 i++, j++, 最后发现 i = 8, j = 5 时也匹配，而此时字符串 B 已经遍历结束了，说明已经在 A 中找到了字符串 B。如果需要找在字符串 A 中出现的位置，i - j 就是结果了，即 下标 3 是 A 开始匹配 B 的起始位置。当然也可以根据 j 的变化不断更新最大值，来判断 B 在 A 中最多连续匹配了多少字符。

怎么求 next 数组？

其实这也是 KMP 算法的核心了，从上面的分析来看，求出 next 数组之后，一切都水到渠成了，那么怎么能求出 next 数组呢？

首先，从上面的分析来看，next[0] = -1, next[1] = 0, 我们引入变量 i, 它表示当前要求的 next 的下标，也是当前遍历到的位置下标，那我们想一下，求 next[i] 需要什么呢？小伙伴们先别往下看，可以试着自己想一下，你一定可以哒，可以自己举例子用笔来比比划划！！！

 

 

答案揭晓，求 next[i] 的时候需要 next[i - 1], 但是，可能只有 next[i - 1] 还不够， 举个例子吧，比如对于字符串 str = "abcdabcad"， 我们在求 next[6] 的时候即要求 "abcdab" 的最长公共前后缀，那么我们可以把该字符串拆成两部分，分别为 "abcda" 和 "b"，我们可以先求出 "abcda" 的公共前后缀，即 next[5]，然后看该公共前后缀后面的字符与字符 'b' 是否相等，

如上图所示，先把 “abcda” 的公共前后缀求出来，即为 “a”, 然后判断前缀 'a' 后面的字符跟后缀 'a' 后面的字符是否相等， 如果相等，那说明 next[6] = next[5] + 1,如上所示，我们看到确实是相等的，两个字符都为 'b'，而 next[5] = 1, 故 next[6] = 2; 这个例子恰好是求了一次 next 就相等了，这样来看是只需要求出来 next[i - 1] 就足够了，但其实是不够的，上述例子是顺利的情况，求了一次 next[i - 1] 之后发现就匹配上了，可是如果求了一次 next 之后还是不相等呢，那还需要再继续求对应的 next，往下循环。

如字符串 "abadababd", 此时需要求 next[8] ，即要求 "abadabab" 的最长公共前后缀，首先求出 next[7], 令 j = next[7], 故 j = 3,而此时 str[3] != str[7], 那么此时需要令 j = next[j],即 j  = next[next[7]],求第二层的 next, 再次进行判断，为什么呢？如下图所示：

先盘点一下我们求了第一次 next 之后得到了什么，首先，我们得到了最长公共前后缀 X 和 Y， 但是 X 后面的字符和 Y 后面的字符不匹配(即str[3] != str[7])，那么我们接下来应该怎么做呢？我们肯定是希望在 X 中找到一个前缀和在 Y 中找到一个后缀，并且这两个前后缀是相同的，这样的话就可以再次进行比较了，如上面 X 中的前缀 "a" 和 Y 中的后缀 "a" 是相同的，那么只需要比较 X 前缀”a“后面的字母是否跟 Y后缀"a"后面的字符是否相等即可，而我们此时发现 X 前缀 "a" 后面的字符是 'b' 与 Y 后面的 'b' 是相同的，故此时可以求出来 next[7] = X 前缀的长度 + 1, 那么 X 前缀的长度等于多少呢，因为其实 X 跟 Y 是相同的，所以说求 X 的前缀跟 Y 的后缀相同的部分，其实就是求 X 的最长公共前后缀，故 X 的前缀的长度即为 next[3]。

还原一下上面的过程，求 next[7] 的时候，我们先找 next[6], 然后发现不匹配， 因为 next[6] = 3, 所以我们再找 next[3], 此时next[3] = 1, 我们发现匹配了，就可以继续往下遍历了。

所以这也就验证了上面所说的，当求了第一次 next 之后发现还是不匹配的时候，那么就继续求 next。如果最后求到 next[0]还是没有匹配，说明没有与该后缀匹配的前缀，故直接设置 next[i] = 0 即可。

next 数组的求解代码模板如下：

public int[] getNext(String str) {
    int[] next = new int[str.length()];
    next[0] = -1;
    char[] strArray = str.toCharArray();
    for (int i = 0; i < str.length() - 1;i++) {
        int j = next[i]; // 这里取 next[i]是因为针对第 0-i 个字符，我们求的是 next[i + 1], 所以跟前面分析的当求 next[i] 时要找 next[i - 1] 还是一致的。
        while (j != -1 && strArray[i] != strArray[j]) {
            j = next[j];
        }

        // 针对第 0 - i 个字符，我们求的是 next[i + 1]
        if (j == -1) {
            next[i + 1] = 0;
        } else {
            next[i + 1] = j + 1;
            
        }
    }
    return next;
}

// 另一个求 next 数组的代码版本

public int[] getNext(String str) {
    int[] next = new int[str.length()];
    next[0] = -1;
    int j = -1; // j 代表 next[i - 1], 初始化为 -1
    int i = 0;
    char[] array = str.toCharArray();
    //要注意，i 的结束条件是 i < array.length - 1, 而不是 i < array.length, 因为我们前面也说过了，next[i] 是对应 0-i-1的字符串，故遍历前 i 个字符的时候，我们求得是 next[i + 1], 所以当遍历到 array.length - 2 的时候，我们就求得了 next[array.length - 1], 就可以停止循环了。
    while (i < array.length - 1) {
        //首先判断 next[i - 1] 对应的字符是否跟当前字符相同。如果相同，则 next[i] = next[i - 1] + 1, 否则，继续求 next
        if (j == -1 || array[i] == array[j]) {
            next[++i] = ++j;
        } else {
            j = next[j];
        }
    }
        
    return next;
}

既然 KMP 算法那么好，为什么 Java 在实现字符串匹配的时候，没有用 KMP 算法？

看了 java 的 String.contains()源码之后，发现 contains() 方法内部调用 String.IndexOf()， 而该方法的实现逻辑就是普通的暴力解法（感兴趣的小伙伴可以去看一下 jdk 的源码），时间复杂度为 O(m*n)，其中 m,n分别为主字符串和模式字符串的长度。为什么呢？其实这个 JDK 不说也就没有标准的答案，大家可以留言区说下自己的想法，这里我说下我的一些看法：

1. 平时我们使用的字符串长度并不长，使用简单的方法已经够我们用了，时间复杂度分析对于数据量越大越有效，但是字符串比较短的时候，不能确定理论时间复杂度比较小的一定效率更高，而上述分析的时间复杂度为 O(m*n) 也是最坏情况的时间复杂度，平均情况下其实够我们用了。
2. KMP 算法还需要额外算出 next 数组，多使用了 O(n) 的空间开销
3. 其实如果字符串真的很长，比如在一篇文章中查询关键敏感字，那这个时候一般也不是仅仅只查一个关键字，这个时候就不应该使用循环反复调用 contains 方法了，而应该用字典树的方法来解决
4. 说了这么多好像学习 KMP 就没什么用和必要了，怎么说呢，其一是我觉得是可以开阔眼界，拓展自己的思维，其二就是它不只是可以用到字符串匹配的问题上来，搞懂 next 数组的思想，他还能在其它地方大放异彩，比如可以解决最小循环节一类的问题，如下面例题 2， 然后其实 next 数组的求法就是用了动态规划的思想，弄懂了 next 数组，对学习动态规划也很有帮助。

 

LeetCode 对应题目：

题目1：28. Implement strStr()

https://leetcode.com/problems/implement-strstr/

该题的意思就是求一个字符串是否在另一个字符串中，如果存在的话就返回它第一次匹配到的位置

解答如下：

class Solution {
    
    public int strStr(String haystack, String needle) {
        if (needle.length() == 0) {
            return 0;
        }
        int[] next = getNext(needle);
        int i = 0, j = 0;
        
        while (i < haystack.length() && j < needle.length()) {
            if (j == -1 || haystack.charAt(i) == needle.charAt(j)) {
                i++;
                j++;
            } else {
                j = next[j];
            }
        }
        
        if (j == needle.length()) {
            return i - j;
        }
        
        return -1;
    }
    
    public int[] getNext(String str) {
        int[] next = new int[str.length()];
        next[0] = -1;
        int j = -1; // j 代表 next[i - 1], 初始化为 -1
        int i = 0;
        char[] array = str.toCharArray();
        
        while (i < array.length - 1) {
            if (j == -1 || array[i] == array[j]) {
                next[++i] = ++j;
            } else {
                j = next[j];
            }
        }
        
        return next;
    }
}

题目2：459. Repeated Substring Pattern

https://leetcode.com/problems/repeated-substring-pattern/

题目大意：判断一个给定的字符串是否可以由多个特定的字符串拼接而成。

代码如下：

class Solution {
    public boolean repeatedSubstringPattern(String s) {
        int[] next = hasNext(s);
        
        if (next[s.length()] * 2 < s.length()) {
            return false;
        }
        
        int common = s.length() - next[s.length()];
        return s.length() % common == 0;
    }
    
    public int[] hasNext(String str) {
        int[] next = new int[str.length() + 1];
        next[0] = -1;
        int j = -1;
        int i = 0;
        char[] strArray = str.toCharArray();
        
        while (i < strArray.length) {
            if (j == -1 || strArray[i] == strArray[j]) {
                next[++i] = ++j;
            } else {
                j = next[j];
            }
        }
        
        return next;
    }
}

代码解析：

1: 该方案借用了 next 数组，然后先判断一下 next[s.length()]  * 2 是否小于 s.length()，如果小于的话，那说明该字符串肯定不是由某个字符串拼接起来的，如某个字符串为 A， 那么两个 A 拼起来是为 "AA", 此时 next[s.length()] * 2 == s.length(),当由多个 A （大于两个）拼接时，结果为 "AAA", "AAAA" ..... 根据最长公共前缀的性质很容易得到 next[s.length()]  * 2  > s.length() 的结论。

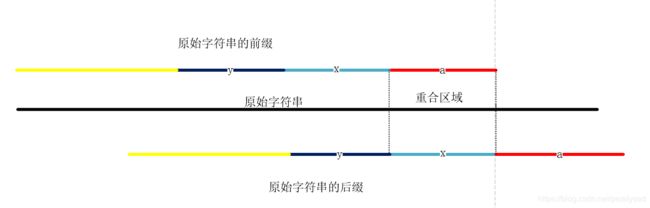
2: 该方案求出了 common = s.length() - next[s.length()]; 然后 s.length() % common 如果等于 0， 说明为 true, 反之结果为 false,为什么呢？

如上图所示，原始字符串即字符串 s, 我们知道，能走到 2 这一步，说明步骤 1 已经成立了，故一定存在前缀的长度和后缀的长度都大于原始字符串长度的 1/2（这里说的前缀后缀对应最长公共前后缀的前缀和后缀）, 即会出现类似上图的形状，此时我们可以盘点一下现在得到了什么，next[s.length()]  = 原始字符串前缀的长度 = 原始字符串后缀的长度。 common = 原始字符串的长度 - 前缀的长度 = a 区域的长度，好，那又因为前缀和后缀是相同的，故前缀中的 a = 后缀中的 a ，（这也是后面用数学归纳法的时候k = 1的情况）, 而参考前缀中 a 对应于原始字符串的区域和后缀中 x 对应原始字符串中的区域是一致的，故 x = a, 又因为前后缀相同的原因，前缀中的 x 等于后缀中的 x， 而此时前缀中 x 对应于原始字符串的区域跟后缀中 y 对应原始字符串中的区域是相同的，故 x = y,此时就从后往前推出了 a = x = y, 故可以按照这个策略一致往后推下去，而如果字符串的总长度是 a 的长度的倍数，s.length() = k*a, 说明再继续往前推，正好还有整数个长度为 a 的区域，那么正好可以推出前缀和后缀中是由整数个 a 拼起来的，可有数学归纳法证明出来，当目前只有 1 个 a 的时候， a = a 显然成立 (上面其实已经推出来了三个 a 的时候成立)，假设当拼成 k 个 a  的时候成立，那么第 k + 1 个 a 的时候也是成立的（就跟上面证明的过程一样，只是在 k 个 a 的基础上往前又推了一个 a ）。

上面证明了当 s.length() 为 a 区域的长度的倍数时，s 就是可以由 k 个 a 区域拼接而成, 那么怎么知道如果不是 a 区域的倍数时他就不行呢？

证明：首先，a 区域是怎么求出来的呢还记得不，a = common = s.length() - next[s.length()] 对吧，而 next[s.length()] 代表的是什么呢？它代表的是最长公共前后缀，而 s.length() 又是固定的，故 common 一定是最小的，也就是说如果 common 不是最小的，那么 next[s.length()] 求出来的就不是最长公共前后缀了，跟 next 数组的定义是有悖的。因此，如果原字符串可以由多个字符串拼接而成，那么最小循环节一定是 a 区域，那么问题就来了，现在只能通过多个 a 来拼接起来，而你整个字符串的长度又不是 a 区域长度的倍数，那你告诉我怎么拼，故当字符串长度不是 a 的倍数的时候，它还真的就是不行。

 

上面我们已经知道了判断字符串是不是可以由某个字符串循环拼接形成，进而也能知道最小循环节为 len - next[len], 然后因此其实还能知道循环的次数 n = len / (len - next[len]), 其实还能引出另一个问题，一个不完整的循环串，需要补多少个字符使其变得完整呢？

证明：接着上面来说，如果此前不是循环串，那么字符串的长度肯定不是 a 区域长度的倍数，也就是说，按照上面的推理过程，当从后往前推出一个一个 a 的时候，肯定最后一段是因为长度不够而没有办法拼成 a 对吧，如下图：

注意上图 a = x = y， 那么我们面临这种情况的时候，只需要把长度不够的那段不完整，形成一个完整的 a 区域就好了，拿字符串 "bbcbbcb", 它的最长公共前后缀为 "bbcb"， a 区域为 "bcb", 长度不够的区域为 "b"， 那么我们需要把 "b" 拼成 "bcb", 需要再添加两个字符，源字符串就变成了 "bcbbcbbcb", 如下图所示：

至此，我们可以知道需要添加的字符的个数为 ：(循环节长度) - 字符串长度%(循环节长度)，其实如果你想的话，还能算出来具体要添加哪些字符。