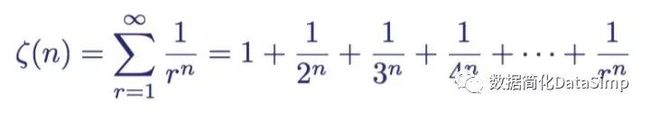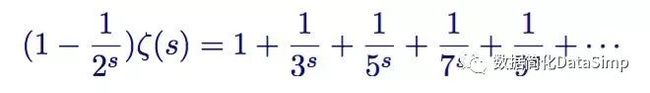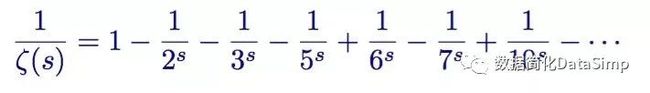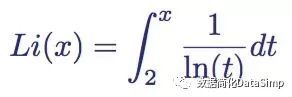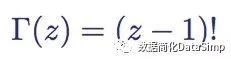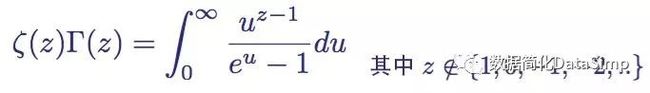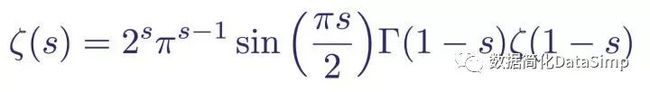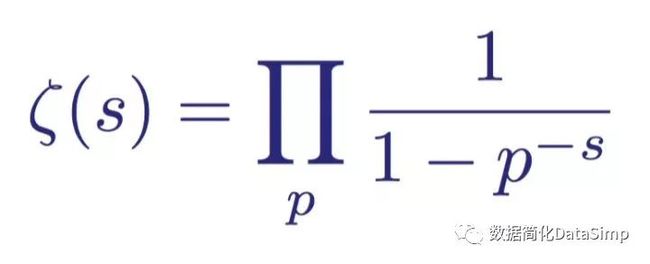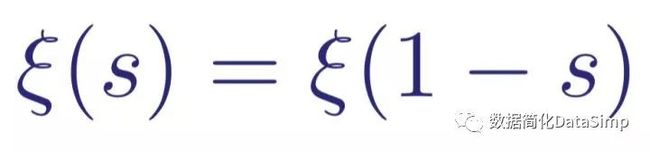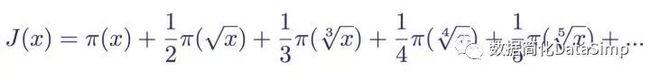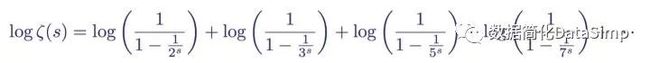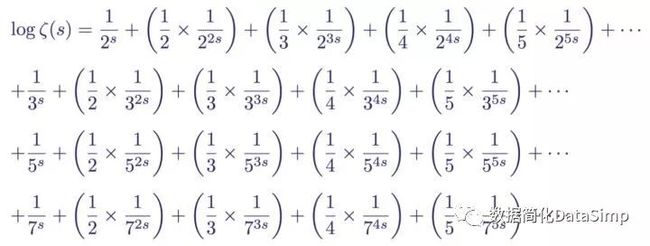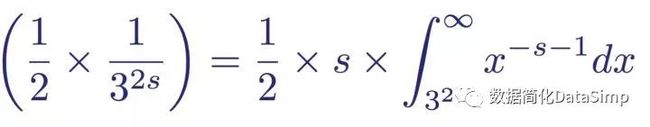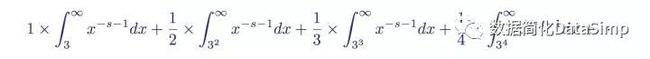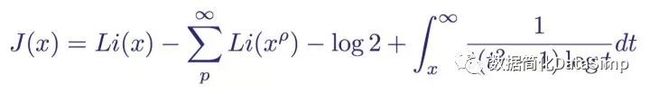自然数简化到素数：黎曼猜想RiemannHypothesis及其解释(公号回复“黎曼猜想”下载PDF经典收藏版彩标资料)

自然数简化到素数：黎曼猜想RiemannHypothesis及其解释(公号回复“黎曼猜想”下载PDF经典收藏版彩标资料)

原创： 秦陇纪 数据简化DataSimp 今天

数据简化DataSimp导读：科学大院《黎曼猜想Riemann Hypothesis简介》来自黄逸文(中国科学院数学与系统科学研究院)，介绍了黎曼猜想RiemannHypothesis大概。知乎译文《黎曼猜想RiemannHypothesis及其解释(上下)》来自Jørgen Veisdal 2013年本科毕业论文，介绍自然数抽象到素数涉及的各种数学理论。两篇宏观、具体风格不同的中外文章，基本上把自然数简化到素数：黎曼猜想RiemannHypothesis及其解释说清楚了。

自然数Natural number用以计量事物的件数或表示事物次序，即用数码0，1，2，3，4，……所表示的数。表示物体个数的数叫自然数，自然数由0开始，一个接一个，组成一个无穷的集体。自然数有有序性，无限性。分为偶数和奇数，合数和质数等。质数prime number又称素数，有无限个。按因数个数分，自然数可分为质数、合数、1和0。

1、质数：只有1和它本身这两个因数的自然数叫做质数。也称作素数。

2、合数：除了1和它本身还有其它的因数的自然数叫做合数。

3、1：只有1个因数。它既不是质数也不是合数。

4、当然0不能计算因数，和1一样，也不是质数也不是合数。

备注：这里是因数不是约数。

也就是说，自然数里面合数都由素数构成，且可被因数分解为一些素数的乘积。简单说，黎曼猜想Riemann Hypothesis是寻找素数(质数)规律的一种假设性猜想。

 

A自然数简化到素数：黎曼猜想RiemannHypothesis及其解释(7764字)

黎曼猜想Riemann Hypothesis简介

文|黄逸文，中国数学会，数据简化DataSimp20180921Fri

1900年，大数学家希尔伯特(Hilbert)在巴黎举办的第二届国际数学家大会上提出了23个数学问题，它为整个二十世纪的数学发展指明了方向。时过境迁，值千禧年之际，美国克雷研究所提出了7个世纪性的数学难题，并慷慨地为每个问题设置了100万美元的奖金。

图2 德国著名数学家希尔伯特(David Hilbert，1862～1943)

当我们回顾这次跨越时空的呼应时，却发现有一个共同的问题，并且已经伴随着数学家们走过了沧桑百年的历程，它就是大名鼎鼎的黎曼猜想。

黎曼猜想究竟有何神奇之处，竟让如此多的数学家为此痴迷和魂牵梦绕？在它那里，又藏着怎样惊世骇俗的秘密？破译这样一个难题，真的会给数学和世界带来激动人心的改变吗？

质数探索

在自然数序列中，质数就是那些只能被1和自身整除的整数，比如2，3，5，7，11等等都是质数。4，6，8，9等等都不是质数。由于每个自然数都可以唯一地分解成有限个质数的乘积，因此在某种程度上，质数构成了自然数体系的基石，就好比原子是物质世界的基础一样。

人们对质数的兴趣可以追溯到古希腊时期，彼时欧几里得用反证法证明了自然数中存在着无穷多个质数，但是对质数的分布规律却毫无头绪。随着研究的深入，人们愈发对行踪诡异的质数感到费解。这些特立独行的质数，在自然数的汪洋大海里不时抛头露面后，给千辛万苦抵达这里的人们留下惊叹后，又再次扬长而去。

1737年，瑞士的天才数学家欧拉(Euler)发表了欧拉乘积公式。在这个公式中，如鬼魅随性的质数不再肆意妄为，终于向人们展示出了其循规蹈矩的一面。

沿着欧拉开辟的这一战场，数学王子高斯(Gauss)和另一位数学大师勒让德(Legendre)深入研究了质数的分布规律，终于各自独立提出了石破天惊的质数定理。这一定理给出了质数在整个自然数中的大致分布概率，且和实际计算符合度很高。在和人们玩捉迷藏游戏两千多年后，质数终于露出了其漂亮的狐狸尾巴。

横空出世

虽然符合人们的期待，质数定理所预测的分布规律和实际情况仍然有偏差，且偏差情况时大时小，这一现象引起了黎曼的注意。

其时，年仅33岁的黎曼(Riemann)当选为德国柏林科学院通信院士。出于对柏林科学院所授予的崇高荣誉的回报，同时为了表达自己的感激之情，他将一篇论文献给了柏林科学院，论文的题目就是《论小于已知数的质数的个数》。在这篇文章里，黎曼阐述了质数的精确分布规律。

没有人能预料到，这篇短短8页的论文，蕴含着一代数学大师高屋建瓴的视野和智慧，以至今日，人们仍然为隐匿在其中的奥秘而苦苦思索。

黎曼Zeta函数

黎曼在文章里定义了一个函数，它被后世称为黎曼Zeta函数，Zeta函数是关于s的函数，其具体的定义就是自然数n的负s次方，对n从1到无穷求和。因此，黎曼Zeta函数就是一个无穷级数的求和。然而，遗憾的是，当且仅当复数s的实部大于1时，这个无穷级数的求和才能收敛(收敛在这里指级数的加和总数小于无穷)。

为了研究Zeta函数的性质，黎曼通过围道积分的方式对该函数做了一个解析延拓，将s存在的空间拓展为复数平面。

研究函数的重要性质之一就是对其零点有深刻的认识。零点就是那些使得函数的取值为零的数值集合。比如一元二次方程一般有两个零点，并且有相应的求根公式给出零点的具体表达式。

黎曼对解析延拓后的Zeta函数证明了其具有两类零点。其中一类是某个三角sin函数的周期零点，这被称为平凡零点；另一类是Zeta函数自身的零点，被称为非平凡零点。针对非平凡零点，黎曼提出了三个命题。

第一个命题，黎曼指出了非平凡零点的个数，且十分肯定其分布在实部大于0但是小于1的带状区域上。

第二个命题，黎曼提出所有非平凡零点都几乎全部位于实部等于1/2的直线上。

第三个命题，黎曼用十分谨慎的语气写到：很可能所有非平凡零点都全部位于实部等于1/2的直线上。这条线，从此被称为临界线。而最后这个命题，就是让后世数学家如痴如醉且寝食难安的黎曼猜想。

有人曾经问希尔伯特，如果500年后能重回人间，他最希望了解的事情是什么？希尔伯特回答说：我想知道，黎曼猜想解决了没有。美国数学家蒙哥马利(Montgomery)曾经也表示，如果有魔鬼答应让数学家们用自己的灵魂来换取一个数学命题的证明，多数数学家想要换取的将会是黎曼猜想的证明。黎曼猜想，俨然就是真理的宇宙里，数学家心目中那颗最璀璨的明星。

黎曼的三个命题

短短八页的论文里，黎曼给后人留下了卓绝非凡的智慧和思想，也为后世留下了魅力无穷的谜团。文章里的证明因为篇幅限制而多被省略，吝惜笔墨的黎曼却让身后数百年的数学大家费尽心思、相形见绌。这篇格局宏大、视野开阔的论文站在了时代的最前沿，其高瞻远瞩的目光和魄力直到今日仍然指引着主流数学界的方向。

在第一个命题的某一步证明里，黎曼用轻松的语气写道：这是不言而喻的普适性的结果。但就是这样一个似乎不值一提的结果，却花费了后人40年的时间苦苦探索。芬兰数学家梅林因为在这一小步上的贡献而名垂青史。此后，在黎曼眼中一笔带过的第一命题最终才由德国数学家蒙戈尔特(Mangoldt)在46年后给出完整的证明。

针对第二命题，黎曼用了相当肯定的语气指出其正确性。遗憾的是，他没有给出任何证明的线索，只是在与朋友的一封通信里提及：命题的证明还没有简化到可以发表的程度。然而黎曼毕竟高估了读者的能力，第二个命题犹如一座巍峨的大山压在了后世数学家的心中，直到今天也踹不过气来。一个半世纪过去了，人们还在为寻找第二命题的证明而陷入深思，似乎丝毫找不到破解它的希望。

更让人们绝望的是，黎曼在论及第三命题时，破天荒地没有使用肯定的语气，而是谨慎地说道：这很有可能是正确的结论。作为复变函数功彪千古的大师，黎曼此时也失去了信心，只能借助试探的口吻表达自己的观点。也正是这个让黎曼犹豫而止步的命题，终成了数学史上最为壮美险峻的奇峰。

有人曾经质疑黎曼是否真的证明了第一和第二命题，他随意写下的结论仅仅是重复法国数学家费马(Fermat)曾经的覆辙：把错误的想法当成了真理。

1637年，爱好数学的大法官费马在一本书的页边写下了他对一个问题的看法：他发现了一个简洁的证明，但是由于纸张太小无法写下来。这就是被后世称为费马猜想的问题，其完整的证明直到358年后的1995年才由英国数学家怀尔斯借助最艰深的现代工具所完成。

但是，人们很快打消了疑虑。从黎曼遗留下来的部分草稿来看，他的数学思想和功力已经远远超越同时代的数学家。即使是几十年后被陆续发现的手稿中体现出来的能力水平，也让当时的数学家难以望其项背。因此，人们有理由相信，这是一个伟大数学家的自信和坦然。

尽管黎曼猜想成立与否不得而知，数学家们还是倾向于它的正确性。一个半世纪以来，人们在假设黎曼猜想成立的情况下，以它作为基石，已经建立了一千多条定理，并且打造了无比辉煌的数论大厦。然而一旦黎曼猜想找到反例被证伪，这些精美的大楼就会如空中楼阁一样昙花一现，最终崩塌，给数论带来灾难性的结果。

质数分布规律

质数作为一类特殊的整数，任性而古怪，它们悄悄地隐藏在浩浩荡荡的自然数列里，以自己独有的奔放奏出魅力四射的音符。这曲神秘的质数音律，不知让多少追寻真理呼唤的人为之陶醉，为之倾注毕生精力，只为找到质数起舞的脚步和节拍。

遗憾的是，骄傲的质数们都是孤独的行者，在数千年的时光里静静地等待着能读懂它的真命天子。从欧拉(Euler)开始，人们终于得以在无边无际的整数世界里一瞥质数的浮光掠影。

黎曼(Riemann)一举揭示了质数最深处的秘密，优雅地给出了质数分布的精确表达式。人们第一次能够近距离窥视质数们在自然界跳舞的规律，是那样的豪放与不羁，平静时如温柔的月光洒在无波的大海，奔腾时又如滔天巨浪倾泻在一叶孤舟，让人爱恨交织、目驰神移。

然而，质数并不是完全随性而为，它的表现始终臣服在黎曼Zeta函数零点的分布规律上。因此，破译黎曼猜想就等于完全确定了质数跳舞的规律和秩序，无疑将开启数论中最激动人心的篇章。也因此，黎曼猜想成了无数人心目中梦想征服的珠穆朗玛峰。登上这座高峰的勇士，也将和历史上最伟大的名字连接在一起，成为后人敬仰和追随的英雄。

在黎曼的时代，质数定理虽然经由高斯(Gauss)和勒让德(Legendre)提出，但却是未经证实的猜想。它让最捉摸不定的质数在阳光下现出了踪迹。当时最杰出的数学大师也为此倾心，试图证明质数定理。

解决质数定理

在黎曼提出的第一个命题里，数学家很容易证明Zeta函数的零点位于实部不小于0，不大于1的带状区域上，但是无法排除实部等于0和1的两条直线。令人惊喜的是，人们很快发现如果能证明黎曼眼中显而易见的第一命题中的某一关键结论，则可以直接证明质数定理。

在黎曼提交论文的36年后，数学家哈达玛(Hadamard)等人不负众望，终于证明了该结论，也顺带解决了质数定理，从而完成了自高斯以来众多数学大师的心愿。

然而黎曼在第一命题里所轻松描述的全部结论，直到46年后的1905年才由蒙戈尔特(Mangoldt)完成。

黎曼猜想的一个小小命题里就蕴含着如此巨大的能量，自此以后，数学家把注意力都集中到了黎曼猜想的攻坚上来。

于是，1900年的巴黎，希尔伯特(Hilbert)代表数学界提出了23个影响深远的问题，黎曼猜想作为第8个问题的一部分而被世人所知。百年轮回，时至今日，23个问题中已经有19个确定解决，还有3个部分解决。黎曼猜想依然如巍峨的奇山，矗立在人类的智力巅峰之上。

鉴于黎曼猜想的巨大难度，人们无法一步征服如此雄伟的山峰，只能在山脚和山腰寻找攀登的线索。一批数学家另辟蹊径，不再驻足于寻求黎曼猜想的证明上，而是去计算黎曼猜想的零点。如果一旦发现某一个零点并不位于实部是0.5的直线上，这就等价于找到一个反例，从而证实黎曼猜想并不成立。

1903年，丹麦数学家第一次算出了前15个非平凡零点的具体数值。在黎曼猜想公布44年后，人们终于看到了零点的模样。毫无意外的是，这些零点的实部全部都是0.5。

1925年，李特尔伍德(Littlewood)和哈代(Hardy)改进了计算方法，算出前138个零点，这基本达到了人类计算能力的极限。

过于庞大的计算量，让后人放弃了继续寻找零点的努力。而为了选择更多的非平凡零点，人们还在黑暗中苦苦摸索。没想到，这一次，曙光来自于黎曼的遗稿。

手稿里的智慧遗产

随着证明黎曼猜想的努力付诸东流，而计算零点的可能也趋于渺茫，数学家陷入了漫长的痛苦期，以至于他们终于开始怀疑黎曼猜想不过是他直觉的猜测，而并没有实际的计算证据。

黎曼时代的数学家喜欢发表他们认为已经成熟的学术成果，而对探索中的理论讳莫如深。因此，很多数学家公开发表的成果只是他们做研究极小一部分，许多价值连城的远见并没对外公布。

这方面，高斯(Gauss)是一个典型。在1898年公布的高斯科学日记里，人们才发现，他的很多思想和成果已经遥遥领先那个时代，但是却因为没有发表而让后世的数学家走了很多弯路。

比如，椭圆函数双周期性理论的结果直到100年后才被后人重新发现。同时，高斯也最早意识到了非欧几何的存在。这样的例子比比皆是。

人们只能从高斯的稿件和信件中去寻找那些依旧蒙尘却隐匿着科学巨匠光辉的成果。

因此，在黎曼猜想面前灰头土脸的数学家把目光投向了黎曼的手稿。遗憾的是，大部分凝聚黎曼心血和洞见的手稿在他去世后被管家付诸一炬，从此人们失去了近距离了解黎曼进行科学思考和创作的机会，也让他卓绝非凡的智慧结晶失去了传承。

黎曼的妻子侥幸抢救出了一小部分手稿，并把它赠送给了黎曼生前的好友戴德金。后来，她担心手稿里可能有黎曼与她的私人信件，又将大部分手稿索回。这些残留的珍贵手稿，最后经由戴德金献给了哥廷根大学图书馆。这也成了黎曼留给后人的珍贵遗产。

很多慕名前去的数学家希望从黎曼的手稿里得到启发，但是，这些手稿太过艰深晦涩，人们止步于此，无法读懂黎曼在天马行空的字里行间所展示出的才能。一代数学大师的遗物，在为将来破译它的人牢牢地守护着秘密。

零点计算的推进

1932年，德国数学家西格尔(Siegel)终于在历经两年的苦苦钻研后，从黎曼的手稿里找到了关键的证据。正是这一证据表明，黎曼对他提出的三个命题有过极其深刻的思考和计算。

西格尔在手稿里发现了黎曼当年随手写下的公式，这个公式今天被称为黎曼-西格尔公式。西格尔也因为让黎曼的公式重现天日而最终获得了菲尔兹奖。

有些数学家甚至认为：如果不是西格尔发现了这个公式，时至今日，它会像埋入沙漠深处的宝藏，再难被后人重新发现。西格尔写下这个公式的那天，距离黎曼在手稿里留下这份遗产已经过去了73年。

黎曼-西格尔公式很快发挥了其巨大的威力，基于这一公式，人们可以很轻松地继续推进零点的计算。

哈代(Hardy)的学生利用西格尔公式把非平凡零点的个数计算到了1041个，人工智能之父图灵推进到了1104个。此后的几十年，在计算机的辅助下，人们继续了零点计算的接力赛。

1966年，非平凡零点已经验证到了350万个。20年后，计算机已经能够算出Zeta函数前15亿个非平凡零点，这些零点无一例外地都满足黎曼猜想。2004年，这一记录达到了8500亿。最新的成果是法国团队用改进的算法，将黎曼Zeta函数的零点计算出了前10万亿个，仍然没有发现反例。

十万亿个饱含着激情和努力的证据再次坚定了人们对黎曼猜想的信心。然而，黎曼Zeta函数毕竟有无穷多个零点，十万亿和无穷大比起来，仍然只是沧海一粟。黎曼猜想的未来在哪里，人们一片茫然，不得而知。与此同时，试图证明黎曼猜想的人们也传来了佳音。

零点的临界线

图3 数学家哈代(Hardy，1877年-1947年)，他证明了黎曼Zeta函数的零点的临界线，这是针对黎曼猜想重大突破

英国数学家哈代首先证明Zeta函数的零点有无穷多个都位于实部是0.5的直线上。这是一个无比震惊的重大突破。在此之前，人们甚至不知道零点的个数是否有限，而哈代的结果则是直接告诉人们，零点的个数不仅是无穷的，而且还有无穷多个零点都位于这条临界线上。但是遗憾的是，人们并不知道临界线外是否存在非平凡零点。

随后，挪威数学家塞尔伯格(Selberg)证明了临界线上的零点个数占全部非平凡零点个数的比例大于零，这意味着临界线上的零点在全部零点的分布中举足轻重。

进一步，美国数学家莱文森(Levinson)引入了独特的方法，证明临界线的零点占全部零点的比例达到了34.74%。

基于莱文森的技巧，美国数学家康瑞(Conrey)在1989年把比例推进到了40%，这也是迄今为止得到的最好结果。

物理世界的奇遇

在理论和计算的突破猛进下，人们开始关注零点在临界线上的分布规律。数学家蒙哥马利(Montgomery)发现零点分布的规律竟然和孪生质数对在数轴上的分布规律类似。受此启发，他写下了一个关联函数来描述这种规律。令人惊奇的是，该函数描述的理论结果和实际计算结果几乎完美地吻合。

蒙哥马利隐约觉得这背后隐藏着巨大的秘密，却又百思不得其解。带着这一疑问，他在1972年访问了普林斯顿高等研究院。

在下午茶的阶段，他偶遇了物理学家戴森(Dyson)。由于彼此研究领域的巨大差异，两人只是礼貌地寒暄了一下。戴森随口问问蒙哥马利研究的课题。他将心中的困惑全盘托出，这差点惊掉了戴森的下巴。原来，让蒙哥马利云里雾里的关联函数正是戴森研究二十年的成果——这不是别的，正是一类随机厄密矩阵本征值的对关联函数。这是一个描述多粒子系统在相互作用下，能级分布规律的函数。

一边是纯数学的黎曼猜想，它关乎的仅仅是一个Zeta函数非零点分布这样最纯碎的数学性质，揭示的是质数在自然数序列里优雅的舞姿和节奏。另一边，却是最现实的物理世界，它连接着量子体系、无序介质和神经网络等等经典的混沌系统。

理论和现实在这里交汇，在封闭的世界里独自发展了两千多年后，作为数学最主要的分支——数论终于将触角探及真实的时空。时至今日，人们对此呈现出的种种不可思议的关联仍然感到匪夷所思。

数学理论照进现实

进入二十一世纪，越来越多的数学理论成果开枝散叶，很多早期被认为无用之用的分支，今日早已经成为现代科技最强有力的工具，为现代科技的发展推波助澜。

曾经被人们束之高阁而偏安一隅的数学研究正化作人们手中的利器，在探索物质世界的途中披荆斩棘，更为人们提供越来越多的思想动力和创造的源泉。

微积分的诞生开启了牛顿机械宇宙观的宏伟时代。人们惊奇地发现：普天之下，莫非王土，原来物理世界并不神秘，也并无不同，即使隐匿在宇宙深空的天体，其运动的规律都臣服在人类制定的法则之下。自此之后，牛顿力学开始大放异彩，基于其原理所发明的蒸汽机和发动机更是直接点燃了第一次工业革命的烈火。

我们今日所享受的信息时代的文明，诸如电脑芯片和万维网都深深地受益于量子力学的发展。这门彻底改变人们生活的科学，却源自于很多数学基础理论的馈赠，从线性代数、矩阵分析、统计学起，到数学家们为了解决五次方程求解问题而发明的群论等等。

基于广义相对论，人们发明了突破地球引力约束的卫星。这使得天地通讯成为可能，也为深空探测、陆海导航打下了基础。人们日益频繁的出行，基于地理位置的GPS导航等等都在为我们的生活提供前所未有的便利。让爱因斯坦流芳千古的广义相对论，其数学原理正是非欧几何(特别是黎曼几何)和张量分析的应用。

自80年代末期，在物理理论中一枝独秀的弦论，因为其大胆和前卫的想法，深受彼时科学家的青睐。这个有望解决相对论和量子力学的大一统理论，已经逐渐在主流科学界激起千层巨浪。弦论蓬勃发展的道路上，我们不难看到微分几何坚定的背影。

2016年，三位物理学家分享了最高的荣誉——诺贝尔奖。他们因发现了物质拓扑相和在拓扑相变理论上的突出贡献而获奖。数学上艰深抽象的拓扑理论第一次也找到了用武之地。

物理学家用这个工具在理论上预测了一种特殊材质的存在，在它身上，人们能观测到匪夷所思的反常量子霍尔效应。基于该效应发现的材料，能够在常温下、无需超强磁场的协助就能自发在某个方向上呈现电阻为零的特性。这让计算机芯片的发展有了无限广袤的空间，从此量子计算机和微型超级计算机的梦想距离我们又近了一大步。

数论：待开垦之地

数学的各大分支都在默默地为前沿科学提供精妙绝伦的应用。遗憾的是，有一门分支陪伴人类走过漫漫两千多年真理探寻的艰辛旅途，却还在其封闭的理论王国里孤芳自赏。作为数学家们最悠久和最忠实的伙伴，不离不弃，它就是数论。

这个数学中最大的分支已经积累了无数深邃的理论成就，当今科技能受益于数论的成果不过就是隐秘在水下的冰山一角。人们都期待着，有朝一日，当冰山融化时，数论的硕果能惠及每一个后世子孙。破冰的希望，很可能就是处于群山之巅的黎曼猜想。

黎曼猜想，只是数论研究里万千瑰丽中的一朵。人们也期盼着，从它和现实世界那让人千丝万缕的关联中，能找到打开果园的钥匙，让世界从此弥漫着果实的芬芳。

黄逸文(中国科学院数学与系统科学研究院)来源：科学大院

 

 

B黎曼猜想RiemannHypothesis及其解释(上下)(12222字)

黎曼猜想，及其解释(上)

文|Jørgen Veisdal 2013年本科毕业论文，OlingCat笨猫一只译于2018-03-31，数据简化DataSimp20180921Fri

献给约翰·纳什

素数

你还记得素数，对吧？它们无法被其他自然数整除？OK。于是我们有了一个3000多年的问题：

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, p。p是多少？31。下一个p呢？是37。之后的p呢？41。接着呢？43。但是……你怎么知道下一个p是什么？

若你能提出一个论点或公式(甚至仅在任何给定的数列中)能预测到下一个素数是什么，你的名字就会与人类思想中最伟大的成就之一永远联系在一起，与牛顿、爱因斯坦和哥德尔比肩。如果能解决素数为何表现出如此的性质，你就永远不用再做任何事情了，永远。

引言

历史上曾有多位数学巨匠研究过素数的性质。从欧几里得对素数无限性的第一个证明，到欧拉将素数与zeta函数联系起来的乘积公式；从高斯与勒让德提出的素数定理公式，到它被阿达马和德拉瓦莱普森证明；依旧占据主导地位的数学家波恩哈德·黎曼则独立为素数理论做出了最大的突破。他对素数的分布做出了新的，前无古人的发现，所有这些都包含在一篇1859年出版的8页论文里，它至今仍是数论中最重要的论文之一。

自该论文出版以来，黎曼的论文一直是素数理论的中心，它确实是素数定理在1896年被证明的主要原因。自此之后，数学家们又找到了几个新的证明，包括塞尔伯格和埃尔多斯的基本证明。然而黎曼关于zeta函数根的猜想依旧成谜。

素数有多少？

先来点儿简单的。我们都知道(除0和1外)一个数字不是素数就是合数。所有合数都由素数构成，且可被因数分解为一些素数的乘积。素数则是该构建过程中的“积木”或“基本元素”。欧几里得在公元前300年证明了素数有无限个。

欧几里得定理

设素数集有限。建立一个所有素数的列表。令P为该列表中所有素数的积(将列表中的所有素数相乘)。将结果数字加一，Q = P + 1。同所有数字一样，数字Q不是素数就是合数：

l  若Q为素数，你就找到了一个不在“所有素数的列表”中的素数。

l  若Q非素数，则为合数，即在列出的所有素数中，存在素数p可整除Q(因为所有合数都是一些素数的乘积)。每个构成P的素数p显然整除P。若p能同时整除P和Q，那么它应当也能整除二者之差，即1。然而没有素数能够整除1，因此p必定不在该素数列表中，这与该列表包含所有素数矛盾。

总存在另一个能整除Q的素数p不在该列表中，因此素数必有无限个。

为何素数如此难以理解？

任何初学者都能理解我前面提出的问题，仅此一点就足以说明它有多么困难。甚至在进行过大量研究后，我们对素数的代数性质仍然知之甚少。科学界十分确信我们缺乏理解素数行为的能力，大数的因式分解(即找出一个数是由哪两个素数相乘所得)便是加密理论的基础之一。下面就是一种寻找它们的方法：

我们已经很好地理解了合数，即所有的非素数。它们由素数构成，你很容易就能写下一个式子来预测和/或生成合数。这样的“合数过滤器”称作一个数筛，最有名的例子便是约公元前200年的“埃拉托斯特尼筛法”。它所做的就是简单地在一个有限集中标记出每个素数的倍数。所以，先取素数 2，并标记出4,6,8,10等，接着取素数3，然后标出6,9,12,15等等，最后就只剩素数了。虽然很好理解，但正如你所料，埃拉托斯特尼筛法并不高效。

函数6n ± 1能显著简化此工作，这个简单的函数会产生除2和3之外的所有素数，并移除所有3的倍数和所有偶数。将n = 1,2,3,4,5,6,7代入会产生结果：5,7,11,13,17,19,23,25,29,31,35,37,41,43。该函数生成的非素数只有25和35，它们分别可被分解为5×5和5×7。如你所料，之后的非素数为49 = 7×7、55 = 5×11等等。挺的简单吧？

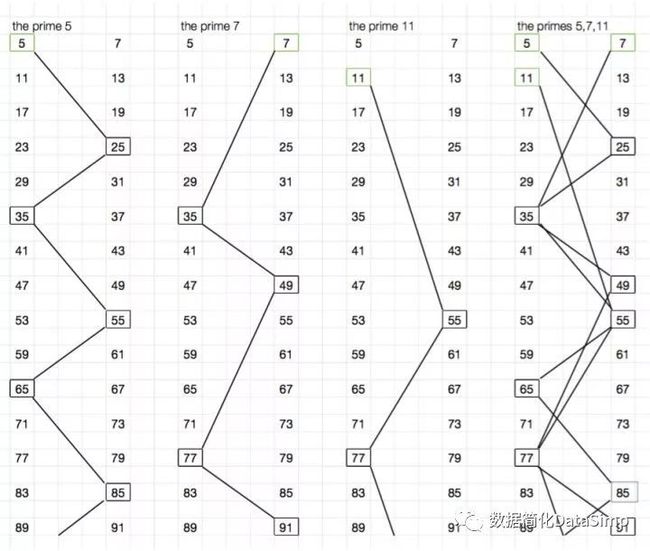
为了从视觉上展示它，我使用了自己称为“合数梯”的东西，它能直观地展现出该函数生成的合数相对于每个素数的布局和组合。在下图的前三列中，你可以清晰地看到素数5, 7, 11与它们各自的合数梯一直到91。第四列的混乱则展示了此筛子如何移除素数以外的所有的数字，它清楚地展现了为何素数如此难以理解。

合数梯子

基础资源

所以这一切都与你可能听说过的“黎曼猜想”有关？嗯...简单来说，为了更好地理解素数，数学家们在19世纪便不再尝试预测素数的精确位置，转而将素数的现象视为一个整体。这种分析的方法就是黎曼所擅长的，他著名的猜想也由此得出。不过在解释它之前，我们有必要先熟悉一些基础资源。

调和级数

调和级数是个无限级数，它首先由尼科尔·奥雷斯姆在14世纪研究。其名字与音乐中谐波的概念有关，即高于基音基本频率的泛音。该级数如下：

无限调和级数的第一项

该和式被奥雷斯姆证明是不收敛的(即不存在极限，不接近/趋向于任何特定的数字，而是一直增长到无穷大)。

Zeta 函数

调和级数是一个更一般形式的，被称为zeta函数ζ(s)的一个特列。zeta函数的实际值由给定的r和n两个实数决定：

zeta函数

若将n = 1代入，就会得到调和级数，它是发散的。然而对于n> 1的所有值, 该级数是收敛的，这意味着当r递增时，其和趋向于某些数，即它不会增长到无穷大。

欧拉乘积公式

zeta函数和素数间的第一个联系是由欧拉发现的，当时他发现了n和p两个自然数(大于零的整数)之间的关系，其中p为素数：

欧拉乘积公式，其中n，p均为大于零的数字且p为素数

该表达式首先出现在1737年一篇题为Variae observationescirca series infinitas(无穷级数的各种观察)的论文中。该表达式陈述了zeta函数的求和等于一减去素数的-s次方的倒数的求积。这种惊人的联系奠定了现代素数理论的基础，即使用zeta函数ζ(s)作为研究素数的方法。

此公式的证明是我最喜欢的证明之一，因此我在这里收录了它，即便它对我们的目的而言并非严格必须的(它太优雅了！)：

欧拉乘积公式的证明

欧拉从一般的zeta函数开始

zeta函数

首先，他将等式两边同时乘以第二项：

zeta 函数乘以1/(2s)

接着他从zeta函数中减去结果表达式：

zeta函数减去1/(2s)乘以zeta函数

他重复这个过程，紧接着在两边同时乘以第三项：

zeta函数减去1/(2s)乘以zeta函数，再乘以1/(3s)

接着从zeta函数中减去结果表达式：

zeta函数减去1/(2s)乘以zeta函数，减去1/(3)再乘以zeta函数

无限重复此过程，最后会留下表达式：

1减去所有素数的倒数，乘以zeta函数

如果你觉得这个过程很眼熟，那是因为欧拉实际上构造了一个筛子，它和埃拉托斯特尼筛法很像。它将非素数从 zeta 函数中筛了出去。接着，将该表达式除以所有素数的倒数项，就得到了：

zeta函数与素数的函数关系，对于前五个素数2,3,5,7和11

简化后，就是：

欧拉乘积公式，该恒等式展示了素数与zeta函数间的联系

是不是非常漂亮？将s = 1代入，就得到了无限调和级数，再次证明了素数的无限。

莫比乌斯函数

奥古斯特·费迪南德·莫比乌斯之后重写了欧拉乘积公式，创造了一个新的求和。除了包含素数的倒数外，莫比乌斯函数也包含了所有可分解为奇数或偶数个质因数的乘积的自然数。他的数中留下的的数字可以被某些素数的平方整除。和式用μ(n)表示如下：

莫比乌斯函数，欧拉乘积公式的一个修改版，在所有的自然数上定义

该和式包含了以下数的倒数：

1.       所有素数；

2.       所有可写为奇数个不同素数的乘积的自然数，前缀一个负号；以及

3.       所有可写为偶数个不同素数的乘积的自然数，前缀一个正号。

以下为第一项：

1除以zeta函数ζ(s)的级数/求和

此和式不包含能够被某些素数的平方(如 4,8,9 等等)整除的倒数。莫比乌斯函数 μ(n) 的值只有三种可能，除了前缀(1 或 -1)外，就是从该和式中移除项(0)：

莫比乌斯函数μ(n)三个可能的取值

尽管莫比乌斯给出了第一个形式化定义，然而这个诡异的和式来自于比它早30多年的高斯的一个旁注，他认为这很不寻常，他写道：

“该和式(对于一个素数p)的所有原根要么≡ 0(当p-1可被一个平方数整除时)，要么≡ ±1 (mod p)(当p-1为不相等的素数的乘积时)；若它们的个数为偶数，其符号为正；若它们的个数为奇数，则符号为负。”

素数计数函数

我们回到素数的问题上。为了理解随着数值的升高素数是如何分布的，我们无需知道它们在哪，只需知道到一个具体的数字为止它们的数量。

高斯引入的素数计数函数π(x)就是做这件事的，它会给出小于或等于一个给定实数的素数的数量。鉴于目前没有已知的寻找素数的公式，我们只能通过图像或每当x为素数时阶跃函数加1的方式来了解素数计数公式。下图显示了x = 200时的函数。

素数计数函数π(x)，其中x = 200

素数定理

素数定理也由高斯(和勒让德独立地)阐述：

素数定理

在汉语(原文英语)中，它被陈述为：“当x增长到无穷大时，素数计数函数π(x)会近似于x/ln(x)函数。换句话说，若你的计数足够大，且将素数数量的图绘制到一个非常大的数x，接着绘制x除以x的自然对数，二者会临近相同的值。两函数图像如下，取x = 1000：

素数计数函数π(x)以及素数定理的估计，绘制到x = 1000

从概率的角度来说，素数定理说明若你随机选择一个自然数x，那么P(x)，即该数字为素数的概率约为1/ln(x)。这意味着前x个整数中连续素数之间的平均间隙约为ln(x)。

对数积分函数

函数Li(x) 在除了x = 1之外的所有正实数上定义。它以一个从2到x的积分定义：

对数积分函数的积分表示

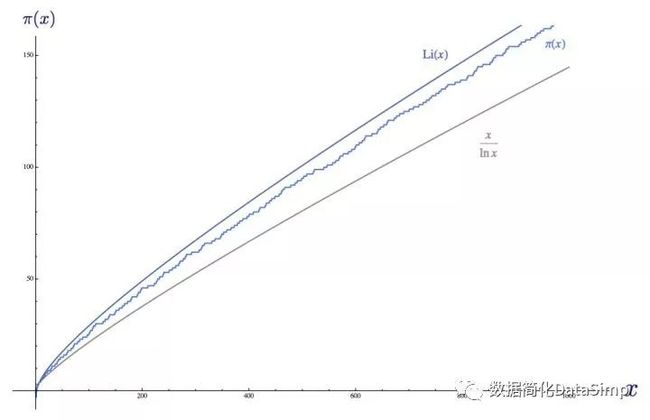
将此函数与素数计数函数和素数定理公式一起绘制，我们会看到其实Li(x)比x/ln(x)近似得更好：

对数积分函数Li(x)，素数计数函数π(x)和x/ln(x)一起绘制

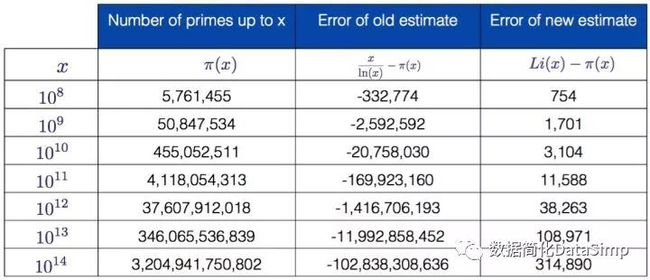
若我们做一个表格，其中包含足够大的x值、到x为止的素数个数以及旧函数(素数定理)与新函数(对数积分)之间的误差，就能看出它近似得有多好：

到一个给定的10的幂的素数个数以及两种估计对应的误差项

从这里可以很容易看出，对数积分函数的近似值远远好于素数定理函数，对于x = 10^14只“猜多了” 314,890个素数。然而，这两个函数都只能向素数计数函数π(x)靠拢。Li(x)靠拢得更快，但随着x增长到无穷大，素数计数函数与Li(x)和x/ln(x)的比率趋向于1。如图所示：

将两个估计和素数计数函数的比率收敛到1，其中x = 10,000

Gamma函数

自丹尼尔·伯努利和克里斯蒂安·哥德巴赫在1720年代研究如何将阶乘函数扩展到非整数参数的问题以来，Gamma函数Γ(z)一直是一个重要的研究对象。它是阶乘函数n!(1×2×3×4×5×...×n)延拓后向下移1：

Gamma函数，在z上定义

它的图像非常古怪：

Gamma函数Γ(z)绘制在范围-6 ≤ z ≤ 6内

Gamma函数Γ(z)在所有实部大于零的复数z上定义。你可能知道，复数是带虚部的一类数，写作Re(z)+ Im(z)，其中Re(z)为实部(普通的实数)，Im(z)为虚部，以字母i表示。一个复数通常写成z= σ + it的形成，其中σ为实部，it为虚部。复数非常有用，因为它们允许数学家和工程师求解和处理普通实数不允许的问题。视觉上，复数将传统的一维“数轴”扩展成二维“数平面”，称之为复平面，其中复数的实部绘制在x轴上，虚部绘制在y轴上。为了能够使用Gamma函数Γ(z)，通常将其形式重写为

Gamma函数Γ(z)的函数关系

通过该恒等式可获得实部小于等于零的z的值。然而它不会给出负整数的值，因为它们没有定义(从技术上说它们是奇异点或简单的极点)。

Zeta与 Gamma

zeta函数与Gamma函数的联系由以下积分给出：

 

黎曼猜想，及其解释(下)

文|Jørgen Veisdal 2013年本科毕业论文，OlingCat笨猫一只译于2018-03-31，数据简化DataSimp20180921Fri

黎曼的工作

现在基础资源已经齐备，我们终于可以建立起素数与黎曼猜想之间的联系了。

德国数学家波恩哈德·黎曼，1826年生于布列斯伦茨。师从高斯的黎曼发表了分析与几何领域的工作。他最大的贡献在微分几何领域，为后来爱因斯坦在广义相对论中使用的几何语言奠定了基础。

他在数论中唯一的成就，论文Ueber dieAnzahl der Primzahlen unter einer gegebenen Grösse，“论小于给定数值的素数个数”被认为是该领域中最重要的论文。他在短短四页中概述了：

l  黎曼zeta函数ζ(s)的定义，一个复值化的zeta函数；

l  zeta函数对于所有复数s≠1的解析延拓；

l  黎曼xi函数ξ(s)的定义，一个通过Gamma函数与黎曼zeta函数建立起联系的整函数；

l  黎曼zeta函数的两个函数方程的证明;

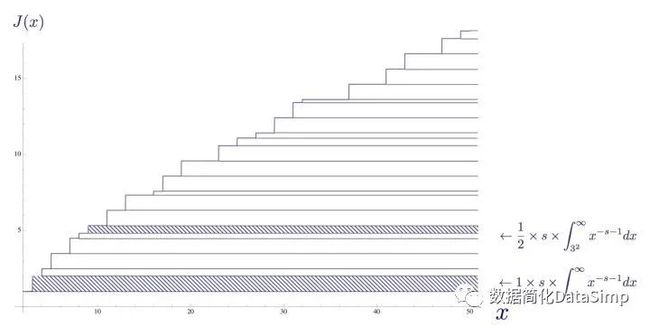
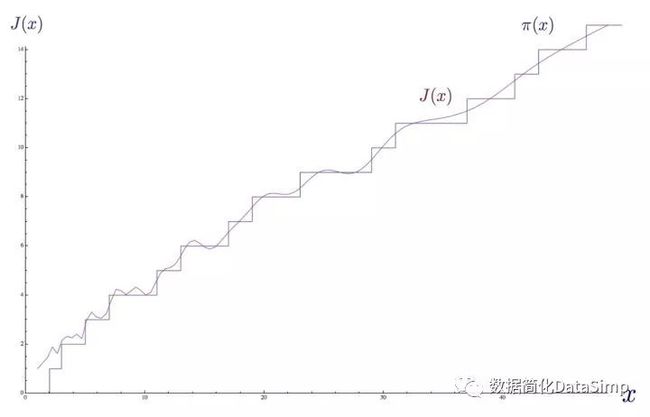
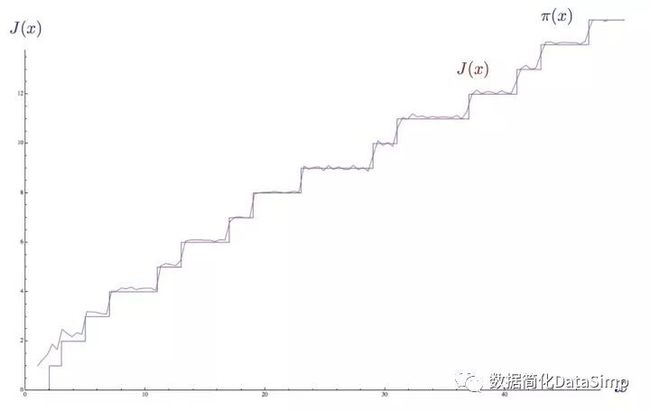
l  黎曼素数计数函数J(x)的定义，通过素数计数函数和莫比乌斯函数定义；

l  通过黎曼zeta函数的非平凡零点定义的黎曼素数计数函数，给出了一个明确的公式来计算小于给定数值的素数个数。

这是个令人难以置信的壮举！这种工程性和创造力大概从来没人见过。绝对惊人！

黎曼zeta函数

我们已经看到了欧拉在它的乘积公式中展示的素数个数与zeta函数之间的紧密联系。然而除了这种关联外，我们对它们的关系知道得并不多，而复数的引入则明确地展示了这二者之间是如何相互联系的。

黎曼是第一个对复变量s考虑zeta函数ζ(s)的人，其中s = σ + it。

黎曼zeta函数对于n，其中s = σ + it为复数，σ和t均为实数。

被称为黎曼zeta函数的ζ(s)，是一个对所有实部大于1的复数(Re(s) > 1)解析(即有可定义的值)的无限级数，在这一区域内，它绝对收敛。

为了分析规则收敛区域(即复变量s的实部大于1)以外的区域中的函数，该函数需要重新定义。黎曼通过对Re(s) > 0半平面中绝对收敛的函数进行解析延拓，成功地做到了这一点。

黎曼zeta函数的重写形式，其中{x} = x-∣x∣

zeta函数的新定义在除s = 1这一奇点/简单极点外的Re(s) > 0半平面上解析。它在该定义域上叫做亚纯函数，因为它除了在简单极点s = 1处以外是全纯的(此定义域中每一个点的领域均可微分)。它也是被称为狄利克雷L-函数的一个很好的例子。

黎曼在他的论文中并未就此止步。它用Gamma函数Γ(z)继续将他的zeta函数解析延拓到了整个复平面。为了保持本文的简洁，我不会在这里展示它的计算过程，但我强烈推荐你自己读一下，它展现了黎曼敏锐的直觉和高超的技术。它的方法利用了Gamma函数Γ(z)对复变量的积分形式和雅可比theta函数ϑ(x)，它们一同重写后会出现zeta函数。zeta函数的解析式为：

对于整个复平面的一个函数式zeta方程，除了s = 0和s = 1两处奇点

在此形式中，可以看出ψ(s)项比x的任何次幂减少得更快，因此该积分对s的所有值收敛。甚至更进一步，黎曼注意到如果用1-s代替s，那么大括号中的第一项是不变的。这样做之后，黎曼就移除了s=0和s=1两处极点，进一步扩展了此方程的用途，并定义了无奇点的黎曼xi函数：

黎曼xi函数ξ(s)

黎曼zeta函数的零点

zeta函数的根/零点(即当ζ(s) = 0 时)可被分为两种类型，分别被称作黎曼zeta函数的“平凡”和“非平凡”零点。

实部Re(s) < 0时存在的零点

平凡零点即容易找到和解释的零点。它们在zeta函数的以下函数形式中最中意注意到：

黎曼的函数式zeta方程的一个变体

当正弦项为零时，该乘积亦为零。kπ处均是如此。因此，例如对于负偶数s= -2n，zeta函数为零。然而对于正偶数s = 2n，零点会与Gamma函数Γ(z)的极点抵消。这在原始的函数形式中更容易看到，若你将s = 2n代入，那么该项的第一部分会是未定义的。

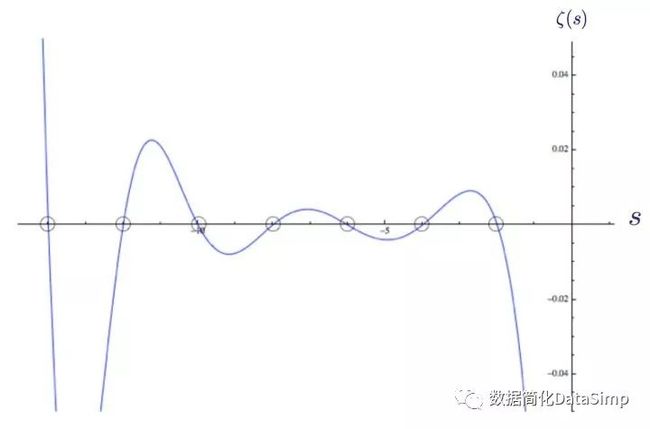
因此，黎曼zeta在每个负偶数s = -2n处都有零点。它们是平凡零点，可在以下函数图像上看到：

标出了s = -2, -4, -6等平凡零点的黎曼zeta函数ζ(s)

实部Re(s) > 1时存在的零点

从zeta的欧拉乘积表示中，我们立刻就会发现ζ(s)在s的实部大于1的区域内不能为零，因为如果其因子之一为零，则收敛的无穷大乘积只能为零，而素数无穷性的证明否定了这一点。

欧拉乘积公式

实部0 ≤ Re(s) ≤ 1时存在的零点

现在我们在Re(s) < 0的负半平面上找到了zeta的平凡零点，并展示了在Re(s) > 1的区域上不可能存在任何零点。然而在这两个区域之间，被称为临界带的区域，几百年来一直占据了分析数论的焦点。

黎曼zeta函数ζ(s)在区间-5 < Re < 2, 0 < Im < 60内实部和虚部的图像

在上图中，我已经将ζ(s)函数的实部绘制成红色，虚部为蓝色。我们看到当s的实部为-2和-4时的两个零点在左下方。在0和1之间，我已经突出了临界带，并标出了zeta函数ζ(s)的实部和虚部相交的地方。它们是黎曼函数的非平凡零点。随着数值的升高，我们会看到更多零点，这两个看似随机的函数也随着s虚部的升高变得越来越稠密。

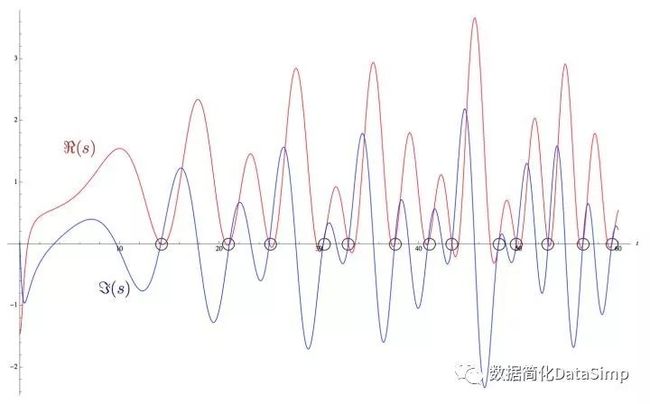
黎曼zeta函数ζ(s)在区间-5

黎曼xi函数

我们已经将黎曼xi函数ξ(s)(移除了奇点的函数方程版本，因此它在s的所有值上定义)定义为：

无奇点的黎曼xi函数

该函数满足关系

黎曼xi函数正负值之间的对称关系

这意味着该函数关于垂线Re(s) = 1/2对称，使得ξ(1) =ξ(0)、ξ(2) = ξ(-1)等等。

此函数关系(s与1-s的对称性)与欧拉乘积公式一同显示了黎曼xi函数ξ(s)只在区间0 ≤ Re(s) ≤ 1内有零点。换句话说，黎曼xi函数的零点对应于黎曼zeta函数的零点。在某种意义上，黎曼zeta函数的临界线R(s) = 1/2对应于黎曼xi函数ξ(s)的实数线(Im(s) = 0)。

任何人只要一看上面这两张图表，立刻就能注意到黎曼zeta函数ζ(s)的非平凡零点(即黎曼xi函数的零点)的实部Re(s)都等于1/2。黎曼在他的论文中简要地提到了这种现象，这一简短的注解，最终将成为他最伟大的遗产之一。

黎曼猜想

黎曼zeta函数ζ(s)非平凡零点的实部Re(s) = 1/2。

这是黎曼在他著名的论文中提出的未证明的推测的现代表述。它指出zeta在临界带0 ≤ Re(s) ≤ 1中的零点，即ζ(s) = 0，均有实部Re(s) = 1/2。若果真如此，那么所有zeta的非平凡零点均有形式ζ(1/2 + it)。一个等价的表述(黎曼的原始表述)为黎曼xi函数ξ(s)的根均为实数。在下图中，直线Re(s) = 1/2为横轴。ζ(s)的实部Re(s)图像为红色，而虚部Im(s)图像为蓝色。非平凡零点为红蓝图像在横轴上的交点。

黎曼zeta函数在直线Re(s) =1/2上的第一个非平凡零点

若黎曼猜想证明为真，则该函数的所有非平凡零点，即两图像的交点均会出现在该直线上。

相信黎曼猜想的理由

我们有很多理由相信黎曼关于zeta函数零点的猜想为真。对数学家而言，也许最吸引人的原因是它对于素数分布的意义。此猜想的数值验证到非常高的值时仍然为真。实际上，该猜想的数值证据已经足够强到在物理和化学这类领域中被视为经过实验验证了。然而，数学史上曾有几个推测，从数值上显示到非常高的值时为真，但仍然被证明是假的。德比夏尔(2004)讲述了斯奎斯数的故事，它给出了一个非常非常大的数值上界，否定了高斯的一个推测，即对数积分Li(x)总是大于素数计数函数。它被利特尔伍德不加反例地证否，然后表明它在非常非常大的斯奎斯数以上必定失效，该数为10的(10的(10的34次方)次方)次方(10^(10^(10^34)))，虽然高斯的猜想已经被证明有误，但要给出一个具体的例子仍远超现今的数值计算能力。对于黎曼猜想来说也是如此，它“只不过才”被验证了十的十二次方个非平凡零点而已。

黎曼zeta函数与素数

以黎曼猜想为真作为起点，黎曼开始研究其意义。他在论文中写道：“……很可能所有根都是实数。当然我们希望对此有一个严格的证明；经过一番短暂而徒劳的尝试后，我将它暂时搁置，因为它对我下的一个研究目标来说并不是必须的。”而他的下一个目标就是将zeta函数的零点与素数联系起来。回忆一下素数计数函数π(x)，它表示包括一个实数x以内的素数个数。黎曼用π(x)来定义他自己的素数计数函数，即黎曼素数计数函数J(x)。它被定义为：

黎曼素数计数函数

首先注意到该函数并非无限。对于某些项，该计数函数将为零，因为在x < 2时没有素数。以J(100)为例，该函数由七项构成，因为第八项对于100会包含一个根8，它约等于1.778279...，因此该素数计数函数项为零，而其和为J(100) = 28.5333...。与素数计数函数一样，黎曼素数计数函数J(x)也是一个阶跃函数，它按照以下规则增加：

黎曼素数计数函数可能的值

为了将J(x)的值与到包括x以内素数的个数联系起来，我们通过一个被称作莫比乌斯反演的过程(我不会在这展示它)恢复素数计数函数。其结果表达式为

素数计数函数π(x)以及它与黎曼素数计数函数和莫比乌斯函数μ(n)的关系

还记得莫比乌斯函数可能的值为

莫比乌斯函数μ(n)的三个可能的值

这意味着我们现在可以将素数计数函数写成一个关于黎曼素数计数函数的函数：

素数计数函数写成关于黎曼素数计数函数的函数，对于前七个n值的图像

这个新的表达式仍然是个有限求和，因为当x < 2时J(x)为零，毕竟没有素数小于2。若我们现在考察J(100)这个例子，会得到和式

素数计数函数对于x = 100

我们得到的就是100以内素数的个数。

欧拉乘积公式的变换

接下来，黎曼以欧拉乘积公式作为起点，推导出一种用微积分的微分语言来分析求解素数个数的方法。从欧拉乘积公式开始：

欧拉乘积公式对于前五个素数的图像

首先两边取对数，然后重写括号中的分母，他推导出关系

欧拉乘积公式的对数重写形式

然后，它用著名的麦克劳林-泰勒级数展开了右边的每一个对数项，创造出一个无限和的无限和，其中每一个无限和都对应于素数级数中的每一项。

对数欧拉乘积公式前四项的泰勒展开

观察其中一项，如：

1/3^s的麦克劳林展开的第二项

这一项，以及其它所有的项都可以用微积分表示成J(x)函数下区域的一部分。写成积分形式：

1/3^s的麦克劳林展开的第二项的积分形式

换句话说，通过欧拉乘积公式，黎曼展示了可以将离散的素数计数函数表示成连续的积分求和。我们的示例项在下图中展现为黎曼素数计数函数下区域的一部分。

黎曼素数计数函数 J(x) 绘制到 x = 50，两个积分已标出

因此，组成了欧拉乘积公式的素数倒数级数的无限积中的每个表达式都可以表示为积分，以此来创建对应于黎曼素计数函数下面积的积分的无穷和。对于素数 3，这个积分的无限积为：

由整数3表示的素数计数函数下构成的区域积分的无穷积

将所有这些无穷和集成一个积分，那么黎曼素数计数函数J(x)下的积分可以简写为：

zeta的对数，表示为积分的无穷级数

或者，更受欢迎的形式：

现代等价的欧拉乘积公式，将zeta函数与黎曼素数计数函数联系起来

黎曼用微积分的语言，通过这种方法将他的zeta 函数ζ(s) 与他的黎曼素数计数函数 J(x) 连接在一个等价于欧拉乘积公式的恒等式中。

误差项

在他得到欧拉乘积公式的分析版本后，黎曼接下来继续创造他自己的素数定理。他给出的明确形式是：

“黎曼素数定理”猜测的在一给定数量x以内的素数个数

这就是黎曼的明确公式。它是对素数定理的改进，能更准确地估计数字x及以内存在多少个素数。该公式有四个项：

第一项，或“主项”为对数积分Li(x)，它是根据素数定理对素数计数函数π(x)更好的估计。它是目前为止最大的项，并且像我们之前看到的那样，它高估了多少包含给定值x以内的素数个数。

第二项，或“周期项”为x的ρ次幂对ρ的对数积分求和(原图误为p，感谢@Idear指正)，它是zeta函数的非平凡零点。它用来调整主项高估的项。

第三项为常量-log(2) = -0.6993147...

第四项，即最后一项是在x < 2上为零的积分，因为没有素数小于2。当该积分约等于0.1400101... 时，它在2处有最大值。

当该函数的值增大时，后两项的贡献是无穷小的。大数的主要“贡献者”是对数积分与周期和。影响见下图：

通过黎曼素数计数函数J(x)的明确公式使用黎曼zeta函数的前35个非平凡零点ρ来近似素数计步函数π(x)

在上图中，我们通过黎曼素数计数函数J(x)的明确公示近似了素数计数函数π(x)，并对zeta函数ζ(s)的前35个非平凡零点求和。我们看到周期项会导致该函数“谐振”并开始接近素数计数函数π(x)的形状。以下为使用了更多非平凡零点的同一图像。

通过黎曼素数计数函数J(x)的明确公式用黎曼zeta函数的前100个非平凡零点ρ来近似素数计步函数π(x)

使用黎曼的显式函数，可以将包括给定数值x以内的素数近似到非常高的精度。实际上，冯·柯赫在1901年证明，使用黎曼猜想的零点来校正对数积分函数，等价于素数定理中误差项的“最佳可能”边界。

“……这些零点就像电线杆，而黎曼zeta函数的特殊性质严格决定了电线必须串连在它们之间……”—Dan Rockmore

结语

自1866年黎曼39岁去世以来，他的突破性论文已经成为素数和分析数论领域的里程碑。到目前为止，尽管伟大的数学家们进行了数百年广泛的研究，然而关于黎曼zeta函数非平凡零点的黎曼猜想仍未解决。每年都会出版与此猜想有关的许多新的结果和猜想，希望有一天它能够确实地得到证明。

本文是JørgenVeisdal 2013年本科毕业论文的重写。论文中引用了很多参考文献，我对此深表感谢，完整论文可从此处http://www.jorgenveisdal.com/files/jorgenveisdal-thesis13.pdf下载。

对于有兴趣进一步探索本主题的人，我特别推荐John Derbyshire的‘PrimeObsession’一书，网址https://www.amazon.com/Prime-Obsession-Bernhard-Greatest-Mathematics/dp/0452285259/。

Prime Obsession: Bernhard Riemann and the GreatestUnsolved Problem in Mathematics Paperback – May 25, 2004 by John Derbyshire (Author), 4.6 out of 5 stars 180 customer reviews. Seeall 6 formats and editions: Hardcover $36.91, 33 Used from $5.08 21 New from$31.83, Paperback $15.84, 84 Used from $2.04 57 New from $11.61. The AmazonBook Review.

译注

译者本人非数学专业，英语刚蹭过四级，所以文中大概存在相当多的翻译和理解问题。若有发现此类问题，恳请斧正。(咱不翻译文章，只是Google翻译+词典的搬运工= =||)

本文已征得原作者JørgenVeisdal (https://medium.com/@JorgenVeisdal/the-riemann-hypothesis-explained-fa01c1f75d3f)翻译授权，译文采用CC-BY-SA4.0方式(https://creativecommons.org/licenses/by-sa/4.0/)共享。

题图来自Visualizingthe Riemann zeta function and analytic continuation (https://youtu.be/sD0NjbwqlYw)，一个非常棒的视频，它以动画的方式讲解了黎曼zeta函数及其解析延拓，强烈推荐！(另有官方中英双语版)，不过国内读者需要。

编辑于2018-03-31，标签：数学、数论、黎曼猜想(Riemann Hypothesis)，文章被以下专栏收录：雾雨魔法店，http://zhuanlan.zhihu.com/marisa/20419321。

数学家黎曼(Bernhard Riemann)是一位英年早逝的德国数学家，出生于1826年去世于1866年，享年还不到40岁。黎曼的一生虽然短暂，却对数学的很多领域都做出了极大贡献。

如何证明哥德巴赫猜想？

哥德巴赫于1742年提出以下猜想：任何一个大于2的偶数都可以表示成两个素数的和。至今该理论未被完全证明。这个看似简单的命题，让很多人想证明他，却感到无从下手。

貌似有一处无伤大雅的翻译不当，原文(page39)是very, very large numbernumber;

showing that even though Gauss’ idea had been provento be wrong, an example of exactly where is far beyond the reach of numericalcalculation even today.

应该是虽然Gauss的猜想已经被证明有误，但要给出一个具体例子仍远超现今数值计算能力。

天啊！居然是本科论文，想想我本科在干什么，惭愧啊！

黎曼素数定理那个公式，貌似是对\rho求和。我是根据原文理解的，楼主这里翻译得有点乱。不过貌似原文里也把求和的\rho写成了p。

日本史上最短的高考题：tan1°是有理数吗？——京都大学2006年高考第六题(理科)

tan1^\circ是有理数吗？10个字，引出了日本高考史上最短的问题当年的考生看到这个问题心里的想法一定是肯定是无理数啊，这他妈还用问？？？妈呀怎么证啊？？？这一题，完全印证了越…

我感觉这翻译特别奇怪……

【Gamma函数Γ(z)在所有大于零的复数z上定义。】(这里严格来说应该加上“实部”吧)

【使用该恒等式可获得对于零以内的z的值。】(“对于零以内”是“实部小于或等于零”)

还有前面有些语句也有不严谨之处，不知是翻译问题还是原文如此。

然而并不懂π(x)是怎么给出素数数量的

π(x)只是用来表示x以内素数的数量的，换句话说，就是愣数= =||

-END-

参考文献(540字)

1.黄逸文.黎曼猜想.[EB/OL]中国数学会,https://mp.weixin.qq.com/s?__biz=MzIxNTk0MzMwOQ==&mid=2247486503&idx=1&sn=1a744dcfff3322e05555be19d56deabb,2018-09-19.

2.Jørgen Veisdal 2013年本科毕业论文.黎曼猜想，及其解释(上).[EB/OL]知乎,https://zhuanlan.zhihu.com/p/25055731,2018-03-31.

3.Jørgen Veisdal 2013年本科毕业论文.黎曼猜想，及其解释(下).[EB/OL]知乎,https://zhuanlan.zhihu.com/p/25222934,2018-03-31.

x.秦陇纪．数据简化社区Python官网Web框架概述；数据简化社区2018年全球数据库总结及18种主流数据库介绍；数据科学与大数据技术专业概论；人工智能研究现状及教育应用；信息社会的数据资源概论；纯文本数据溯源与简化之神经网络训练；大数据简化之技术体系．[EB/OL]数据简化DataSimp(微信公众号)，http://www.datasimp.org，2017-06-06．

自然数简化到素数：黎曼猜想RiemannHypothesis及其解释 (20633字)

秦陇纪

简介：自然数简化到素数：黎曼猜想RiemannHypothesis及其解释。(公号回复“黎曼猜想”，文末“阅读原文”可下载94图23k字27页PDF报告)蓝色链接“数据简化DataSimp”关注后下方菜单有文章分类页。作者：黄逸文Jørgen Veisdal等。来源：中国数学会黄逸文科普文章、Jørgen Veisdal 2013年本科毕业论文，数据简化社区秦陇纪微信群聊公众号，引文出处附参考文献。主编译者：秦陇纪，数据简化、科学Sciences、知识简化新媒体创立者，数据简化社区创始人OS架构师/C/Java/Python/Prolog程序员，IT教师。每天大量中英文阅读/设计开发调试/文章汇译编简化，时间精力人力有限，欢迎转发/赞赏/加入支持社区。版权声明：科普文章仅供学习研究，公开资料©版权归原作者，请勿用于商业非法目的。秦陇纪2018数据简化DataSimp综合汇译编，投稿合作、转载授权、侵权错误(包括原文错误)等请联系[email protected]沟通。欢迎转发：“数据简化DataSimp、科学Sciences、知识简化”新媒体聚集专业领域一线研究员；研究技术时也传播知识、专业视角解释和普及科学现象和原理，展现自然社会生活之科学面。秦陇纪发起期待您参与各领域~ 强烈谴责超市银行、学校医院、政府公司肆意收集、滥用、倒卖公民姓名、身份证号手机号、单位家庭住址、生物信息等隐私数据！

自然数简化到素数：黎曼猜想RiemannHypothesis及其解释 (20633字)目录

A自然数简化到素数：黎曼猜想RiemannHypothesis及其解释(7764字)

B黎曼猜想RiemannHypothesis及其解释(上下)(12222字)

参考文献(540字)Appx(845字).数据简化DataSimp社区简介

Appx(845字).数据简化DataSimp社区简介

信息社会之数据、信息、知识、理论持续累积，远超个人认知学习的时间、精力和能力。应对大数据时代的数据爆炸、信息爆炸、知识爆炸，解决之道重在数据简化(Data Simplification)：简化减少知识、媒体、社交数据，使信息、数据、知识越来越简单，符合人与设备的负荷。数据简化2018年会议(DS2018)聚焦数据简化技术(Data Simplification techniques)：对各类数据从采集、处理、存储、阅读、分析、逻辑、形式等方ose 做简化，应用于信息及数据系统、知识工程、各类Python Web框架、物理空间表征、生物医学数据，数学统计、自然语言处理、机器学习技术、人工智能等领域。欢迎投稿数据科学技术、简化实例相关论文提交电子版(最好有PDF格式)。填写申请表加入数据简化DataSimp社区成员，应至少一篇数据智能、编程开发IT文章：①高质量原创或翻译美欧数据科技论文；②社区网站义工或完善S圈型黑白静态和三彩色动态社区LOGO图标。论文投稿、加入数据简化社区，详情访问www.datasimp.org社区网站，网站维护请投会员邮箱[email protected]。请关注公众号“数据简化DataSimp”留言，或加微信QinlongGEcai(备注：姓名/单位-职务/学校-专业/手机号)，免费加入投稿群或”科学Sciences学术文献”读者微信群等。长按下图“识别图中二维码”关注三个公众号(搜名称也行，关注后底部菜单有文章分类页链接)：

数据技术公众号“数据简化DataSimp”：

科普公众号“科学Sciences”：

社会教育知识公众号“知识简化”：

(转载请写出处：©秦陇纪2010-2018汇译编，欢迎技术、传媒伙伴投稿、加入数据简化社区！“数据简化DataSimp、科学Sciences、知识简化”投稿反馈邮箱[email protected]。)

普及科学知识，分享到朋友圈

转发/留言/打赏后“阅读原文”下载PDF

阅读原文

微信扫一扫
关注该公众号