cv论文笔记(动作识别1):Convolutional Two-Stream Network Fusion for Video Action Recognition
一、基本信息
标题:Convolutional Two-Stream Network Fusion for Video Action Recognition
时间:2016
引用格式:Feichtenhofer C, Pinz A, Zisserman A. Convolutional two-stream network fusion for video action recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 1933-1941.
二、研究背景
本文是对标准原始2-steam网络进行改进,和原始2-steam网络在softmax后融合分数不同的是,本文提出在卷积层进行融合,以此学习在空间域和时间域的融合关系,而后再把这种融合关系应用到网络中。
视频动作识别领域卷积神经网络还不如向人脸识别,物体分类,动作识别领域那么表现优秀。原因:
- 一个原因是训练数据太少或者噪音太多。和图像分类相比,视频动作识别还受到运动和视角的影响。所以可能需要更多的训练样本。
- 另一个原因是卷积神经网络架构目前还不能很好的对时间域的信息进行有效利用,目前作用还是集中在空间域,比如物体识别。
而Two-Stream的架构通过独立的训练两个卷积神经网络:
通过分别为静态图像的外观和堆叠的光流独立的训练ConvNets。
分为两个流:
- 空间流处理静止图像帧,得到形状信息
- 时间流处理连续多帧稠密光流,得到运动信息
两个流最后经过SoftMax后,做分类分数的融合
缺点:
- 无法学习到时间特征和空间特征的像素间的对应关系
- 如何随时间演变的(对时间维度的利用很有限,空间网络只用了1帧,时间网络只用了10帧)
空间流卷积网络:
输入的就是一帧,因此可以用ImageNet预训练,识别动作
时间流卷积网络:

上图计算2帧之间的位移向量(上图蓝色窗口的位移在c中), I τ ∈ R w × h × 2 L I_{\tau} \in \mathbb{R}^{w \times h \times 2 L} Iτ∈Rw×h×2L
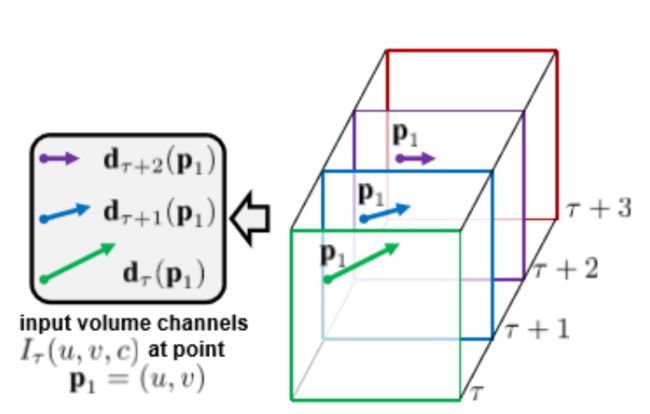
光流堆: 图片w * h中每个位置p有L*2层(*2代表分为x和y方向位移)
I τ ( u , v , 2 k − 1 ) = d τ + k − 1 x ( p k ) I τ ( u , v , 2 k ) = d τ + k − 1 y ( p k ) , u = [ 1 ; w ] , v = [ 1 ; h ] , k = [ 1 ; L ] \begin{array}{l} I_{\tau}(u, v, 2 k-1)=d_{\tau+k-1}^{x}\left(\mathbf{p}_{k}\right) \\ I_{\tau}(u, v, 2 k)=d_{\tau+k-1}^{y}\left(\mathbf{p}_{k}\right), \quad u=[1 ; w], v=[1 ; h], k=[1 ; L] \end{array} Iτ(u,v,2k−1)=dτ+k−1x(pk)Iτ(u,v,2k)=dτ+k−1y(pk),u=[1;w],v=[1;h],k=[1;L]

运动轨迹堆:有递推式
p 1 = ( u , v ) ; p k = p k − 1 + d τ + k − 2 ( p k − 1 ) , k > 1 \mathbf{p}_{1}=(u, v) ; \quad \mathbf{p}_{k}=\mathbf{p}_{k-1}+\mathbf{d}_{\tau+k-2}\left(\mathbf{p}_{k-1}\right), k>1 p1=(u,v);pk=pk−1+dτ+k−2(pk−1),k>1
三、创新点
空间域融合(Spatial fusion)
融合方式:
Sum fusion y s u m = x t a + x t b y s u m ∈ R H × W × D Max fusion y max = max ( x t a , x t b ) y max ∈ R H × W × D Concat fusion y cat = cat ( 3 , x t a , x t b ) y cat ∈ R H × W × 2 D Conv fusion y conv = y cat ∗ f + b f ∈ R 1 × 1 × 2 D × D , b ∈ R D y conv ∈ R H × W × D Biliner fusion y bil = ∑ j = 1 M ∑ i = 1 M x i , j a ⊗ x i , j b y b i l ∈ R D × D \begin{array}{ccc} \text { Sum fusion } & y^{s u m}=x_{t}^{a}+x_{t}^{b} & y^{s u m} \in R^{H \times W \times D} \\ \text { Max fusion } & y^{\max }=\max \left(x_{t}^{a}, x_{t}^{b}\right) & y^{\max } \in R^{H \times W \times D} \\ \text { Concat fusion } & y^{\text {cat }}=\operatorname{cat}\left(3, x_{t}^{a}, x_{t}^{b}\right) & y^{\text {cat }} \in R^{H \times W \times 2 D} \\ \text { Conv fusion } & y^{\text {conv }}=y^{\text {cat }} * f+b & \begin{array}{c} f \in R^{1 \times 1 \times 2 D \times D}, b \in R^{D} \\ y^{\text {conv }} \in R^{H \times W \times D} \end{array} \\ \text { Biliner fusion } & y^{\text {bil }}=\sum_{j=1}^{M} \sum_{i=1}^{M} x_{i, j}^{a} \otimes x_{i, j}^{b} & y^{b i l} \in R^{D \times D} \end{array} Sum fusion Max fusion Concat fusion Conv fusion Biliner fusion ysum=xta+xtbymax=max(xta,xtb)ycat =cat(3,xta,xtb)yconv =ycat ∗f+bybil =∑j=1M∑i=1Mxi,ja⊗xi,jbysum∈RH×W×Dymax∈RH×W×Dycat ∈RH×W×2Df∈R1×1×2D×D,b∈RDyconv ∈RH×W×Dybil∈RD×D
连接方式比较:
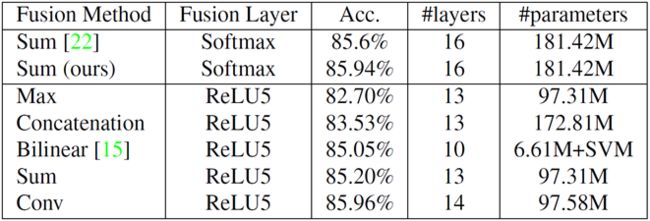
sum和max没有改变维数D
cat保留了2个网络,因此通道数为2D,全连接参数翻倍
conv在cat基础上卷积,卷积核的通道就是2D,数目D个,因此通道又变为D,但是增加了卷积参数和偏置项b
bil没太明白原理,D维叉乘的意义是什么呢
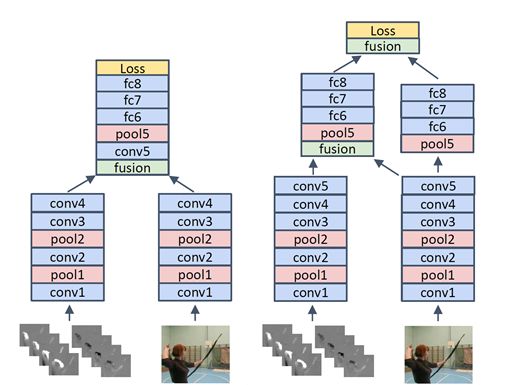
融合位置:
上边的例子展示了在conv4之后的fusion。
而右边的例子展示了两次融合。分别在conv5和fc8。右边的例子最后在第一次融合后,仍然独立保持了两个网络,一个是时空混合的网络,一个是独立的空间的网络。
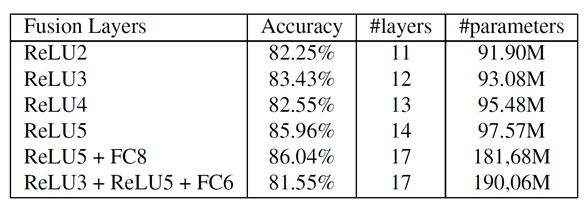
融合太浅的层会减弱效果,比如最后一行
时间域融合(Temporal fusion)
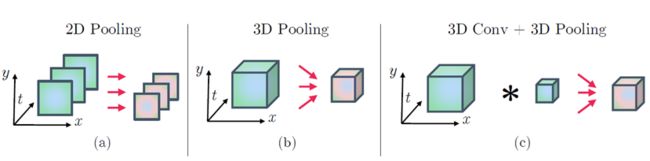
2D Pooling:把网络对不同时刻的预测值进行平均。这种架构只是在2D上进行pooling 。
3D Pooling:用max-pooling对一个大小为 W‘ * H’ * T‘ 的立方体进行3D pooling。
3D Conv+Pooling: 用个filter组成的f( W * H * T* D * D‘ )对四维(W * H * T * D)的input x 进行卷积,加上一个biases ,输出y = x * f + b ( D‘ )然后再接3D pooling。 f的作用是对局部时空features的融合权重化。
总体结构
卷积学习时域(绿)和空域(蓝)的权重(对应关系),同时也能学习局部x, y, t权重。
融合后的时空流和独立的时域流都在通过在时间和空间上的3D pooling去学习时空(左)以及独立的时域(右)features,然后用来识别输入的视频。
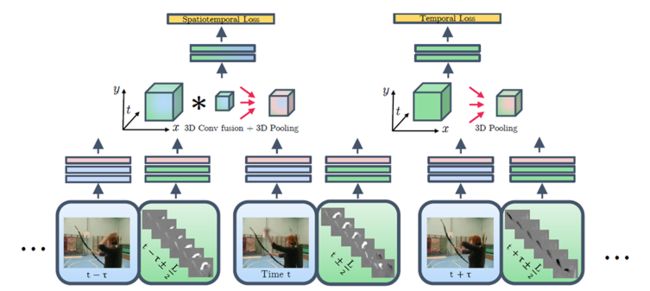
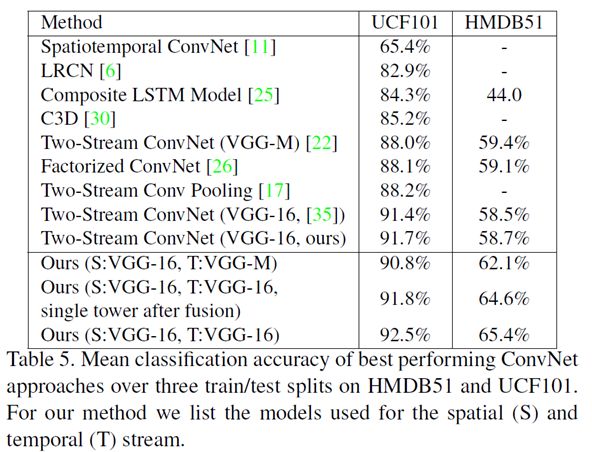
四、实验结果
五、结论与思考
作者结论
总结
与以前的方法相比,新的结构没有显著增加参数的数量,但在两个标准基准数据集上超过了现有的水平。
结果表明,在空间和时间上高度抽象的卷积网络特征之间的学习对应关系的重要性。