图像增强：对比度受限直方图均衡化CLAHE

绪：

直方图均衡简单、高效；

但是，图像中不同的区域灰度分布相差甚远，对它们使用同一种变换常常产生不理想的效果；

实际应用中，常常需要增强图像的某些局部区域的细节。

为了解决这类问题，Pizer等提出了局部直方图均衡化的方法(AHE)；

AHE方法仅仅考虑了局部区域的像素，忽略了图像其他区域的像素，且对于图像中相似区域具有过度放大噪声的缺点；

K. Zuiderveld等人提出了对比度受限CLAHE的图像增强方法；

通过限制局部直方图的高度来限制局部对比度的增强幅度，从而限制噪声的放大及局部对比度的过增强；

也可以被用来对图像去雾操作；

CLAHE和AHE的区别在于前者对区域对比度进行了限制，且采用插值来加快计算；

 

 

1、CLAHE算法原理：

CLAHE与AHE不同的地方是对比度限幅，为了克服AHE的过度放大噪声的问题；

①设自适应直方图均衡化方法的滑动窗口大小为M*M，则局部映射函数为:

 

为滑动窗口局部直方图的累积分布函数(cumulative distribution function);

②的导数为直方图，从而局部映射函数的斜率S为:

 

故，限制直方图高度就等效于限制局部映射函数的斜率，进而限制对比度强度；

③设限定最大斜率为Smax，则允许的直方图高度最大为：

 

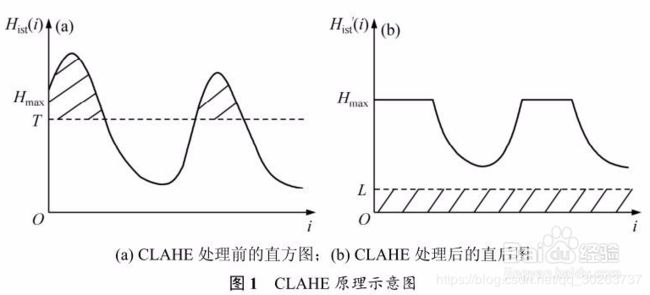
④对高度大于Hmax的直方图应截去多余的部分；

实际处理中，设截取阈值T(而非Hmax)对直方图进行截断，将截去的部分均匀的分布在整个灰阶范围上，以保证总的直方图面积不变，从而使整个直方图上升高度L，则有：

 

⑤最后改进的直方图为：

 

综上所述，改变最大的映射函数斜率Smax及相应的最大直方图高度Hmax，可获得不同增强效果的图像；

CLAHE通过限制局部直方图的高度来限制局部对比度的增强幅度，从而限制噪声的放大和局部对比度的过增强。

 

 

 

2、插值加速方法：

AHE方法，不管是否带有对比度限制，都需要对图像中的每个像素计算其领域及变换函数，算法耗时严重；

对其进行插值加速，使算法效率有极大提升，且质量没有下降；

①将图像均匀分成等份矩阵大小，常见8行8列64块；

②计算每个块的直方图，CDF，变换函数；

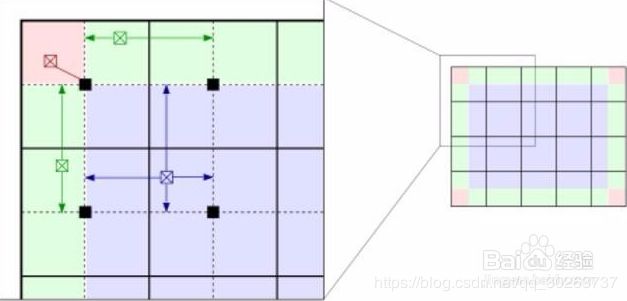
对于块的中心像素(黑色小方块)是完全符合定义的；

③对其他的像素通过其邻近的四个黑色小方块的变换函数插值来获取；

位于中间的像素(蓝色阴影)采用双线性插值；

位于边缘的部分(绿色阴影)采用线性插值；

位于角点处的部分(红色阴影)采用块所在的变换函数；

	Mat src1 = imread("C:\\Users\\aa\\Desktop\\DSC00024.JPG", 1);

	Mat bgr_image = src1;
	if (!bgr_image.rows) {
		cout << "imread failed!" << endl;
	}

	Mat lab_image;
	cvtColor(bgr_image, lab_image, CV_BGR2Lab);

	// 提取L通道
	vector lab_planes(3);
	split(lab_image, lab_planes);

	// CLAHE 算法
	Ptr clahe = createCLAHE();
	clahe->setClipLimit(4);
	Mat dst;
	clahe->apply(lab_planes[0], dst);
	dst.copyTo(lab_planes[0]);
	merge(lab_planes, lab_image);

	//恢复RGB图像
	Mat image_clahe;
	cvtColor(lab_image, image_clahe, CV_Lab2BGR);


	cvtColor(image_clahe, image_clahe, CV_BGR2GRAY);


	threshold(image_clahe, image_clahe, 170, 255, THRESH_BINARY);