模拟退火算法解决TSP问题+Python实现
网上看见的比喻:
爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
旅行商问题 ( TSP,Traveling Salesman Problem ) :有N个城市,要求从其中某个问题出发,唯一遍历所有城市,再回到出发的城市,求最短的路线。
旅行商问题属于所谓的NP完全问题(是世界七大数学难题之一。NP的英文全称是Non-deterministicPolynomial的问题,即多项式复杂程度的非确定性问题),精确的解决TSP只能通过穷举所有的路径组合,其时间复杂度是O(N!) 。
求解旅行商问题的已有算法很多:
- 精确算法如线性规划方法、动态规划方法、分支定界方法;
- 近似方法有插入法、最近邻算法、Clark&Wright算法、生成树法、Chrisrofides算法、r-opt算法、混合算法、概率算法等。
- 近年来的一些尝试:紧急搜索方法、遗传算法、模拟退火算法、神经网络方法、蚁群算法等。
使用模拟退火算法可以比较快的求出TSP的一条近似最优路径。模拟退火解决TSP的思路:
- 产生一条新的遍历路径P(i+1),计算路径P(i+1)的长度L( P(i+1))
- 若L(P(i+1))< L(P(i)),则接受P(i+1)为新的路径,否则以模拟退火的那个概率接受P(i+1) ,然后降温
- 重复步骤1,2直到满足退出条件
产生新的遍历路径的方法有很多,下面列举其中3种:
- 随机选择2个节点,交换路径中的这2个节点的顺序。
- 随机选择2个节点,将路径中这2个节点间的节点顺序逆转。
- 随机选择3个节点m,n,k,然后将节点m与n间的节点移位到节点k后面。
python 3.6.1 代码如下
import numpy as np
import matplotlib.pyplot as plt
import pdb
"旅行商问题 ( TSP , Traveling Salesman Problem )"
coordinates = np.array([[565.0,575.0],[25.0,185.0],[345.0,750.0],[945.0,685.0],[845.0,655.0],
[880.0,660.0],[25.0,230.0],[525.0,1000.0],[580.0,1175.0],[650.0,1130.0],
[1605.0,620.0],[1220.0,580.0],[1465.0,200.0],[1530.0, 5.0],[845.0,680.0],
[725.0,370.0],[145.0,665.0],[415.0,635.0],[510.0,875.0],[560.0,365.0],
[300.0,465.0],[520.0,585.0],[480.0,415.0],[835.0,625.0],[975.0,580.0],
[1215.0,245.0],[1320.0,315.0],[1250.0,400.0],[660.0,180.0],[410.0,250.0],
[420.0,555.0],[575.0,665.0],[1150.0,1160.0],[700.0,580.0],[685.0,595.0],
[685.0,610.0],[770.0,610.0],[795.0,645.0],[720.0,635.0],[760.0,650.0],
[475.0,960.0],[95.0,260.0],[875.0,920.0],[700.0,500.0],[555.0,815.0],
[830.0,485.0],[1170.0, 65.0],[830.0,610.0],[605.0,625.0],[595.0,360.0],
[1340.0,725.0],[1740.0,245.0]])
#得到距离矩阵的函数
def getdistmat(coordinates):
num = coordinates.shape[0] #52个坐标点
distmat = np.zeros((52,52)) #52X52距离矩阵
for i in range(num):
for j in range(i,num):
distmat[i][j] = distmat[j][i]=np.linalg.norm(coordinates[i]-coordinates[j])
return distmat
def initpara():
alpha = 0.99
t = (1,100)
markovlen = 1000
return alpha,t,markovlen
num = coordinates.shape[0]
distmat = getdistmat(coordinates) #得到距离矩阵
solutionnew = np.arange(num)
#valuenew = np.max(num)
solutioncurrent = solutionnew.copy()
valuecurrent =99000 #np.max这样的源代码可能同样是因为版本问题被当做函数不能正确使用,应取一个较大值作为初始值
#print(valuecurrent)
solutionbest = solutionnew.copy()
valuebest = 99000 #np.max
alpha,t2,markovlen = initpara()
t = t2[1]
result = [] #记录迭代过程中的最优解
while t > t2[0]:
for i in np.arange(markovlen):
#下面的两交换和三角换是两种扰动方式,用于产生新解
if np.random.rand() > 0.5:# 交换路径中的这2个节点的顺序
# np.random.rand()产生[0, 1)区间的均匀随机数
while True:#产生两个不同的随机数
loc1 = np.int(np.ceil(np.random.rand()*(num-1)))
loc2 = np.int(np.ceil(np.random.rand()*(num-1)))
## print(loc1,loc2)
if loc1 != loc2:
break
solutionnew[loc1],solutionnew[loc2] = solutionnew[loc2],solutionnew[loc1]
else: #三交换
while True:
loc1 = np.int(np.ceil(np.random.rand()*(num-1)))
loc2 = np.int(np.ceil(np.random.rand()*(num-1)))
loc3 = np.int(np.ceil(np.random.rand()*(num-1)))
if((loc1 != loc2)&(loc2 != loc3)&(loc1 != loc3)):
break
# 下面的三个判断语句使得loc1 loc2:
loc1,loc2 = loc2,loc1
if loc2 > loc3:
loc2,loc3 = loc3,loc2
if loc1 > loc2:
loc1,loc2 = loc2,loc1
#下面的三行代码将[loc1,loc2)区间的数据插入到loc3之后
tmplist = solutionnew[loc1:loc2].copy()
solutionnew[loc1:loc3-loc2+1+loc1] = solutionnew[loc2:loc3+1].copy()
solutionnew[loc3-loc2+1+loc1:loc3+1] = tmplist.copy()
valuenew = 0
for i in range(num-1):
valuenew += distmat[solutionnew[i]][solutionnew[i+1]]
valuenew += distmat[solutionnew[0]][solutionnew[51]]
# print (valuenew)
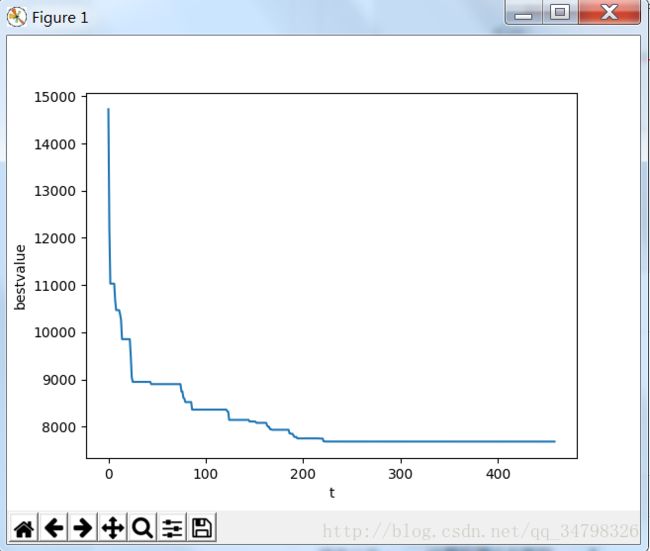
if valuenew 实验结果: