Gamma分布和逆Gamma分布
Gamma分布和逆Gamma分布
- Gamma分布
- Gamma function
- 参数
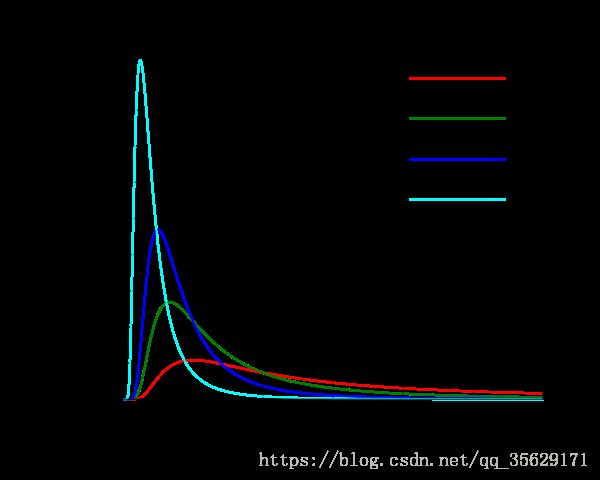
- 图形
- Probability density function
- Cumulative distribution function
- parameters
- Inv-Gamma分布
- 图形
- Probability density function
- Cumulative distribution function
- parameters
- Gamma分布与逆Gamma分布
- 图像python代码 [^1]
- Gamma 分布
- 逆Gamma分布
Gamma分布
If n n n is a positive integer,
Γ ( n ) = ( n − 1 ) ! \Gamma(n)=(n-1)! Γ(n)=(n−1)!
The gamma function is defined for all complex numbers except the non-positive integers. For complex numbers with a positive real part, it is defined via a convergent improper integral:
(伽马函数是为除非正整数之外的所有复数定义的。 对于具有正实部的复数,它通过收敛的不正确积分来定义:)
Γ ( z ) = ∫ 0 ∞ x z − 1 e − x d x \Gamma(z)= \int_0^\infty x^{z-1}e^{-x}dx Γ(z)=∫0∞xz−1e−xdx
Gamma function
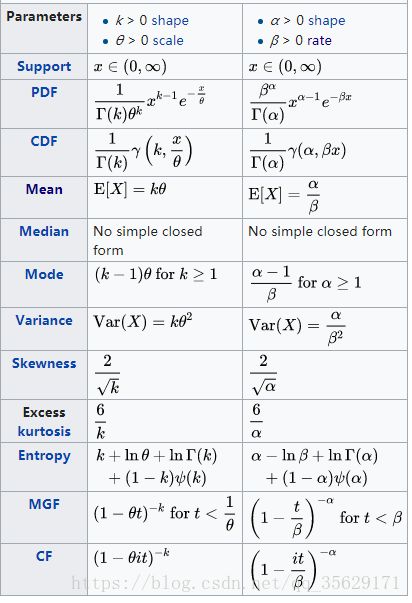
参数
参数 α \alpha α,成为形状参数(shape parameter),决定了分布曲线的形状,也就是 α \alpha α不同,分布曲线形状不同
参数 β \beta β成为尺度参数(scale parameter),在其他参数一定时, β \beta β不同,分布曲线的形状相似,但是高低、胖瘦不同,或者说是同一形状按照比例放大或缩小
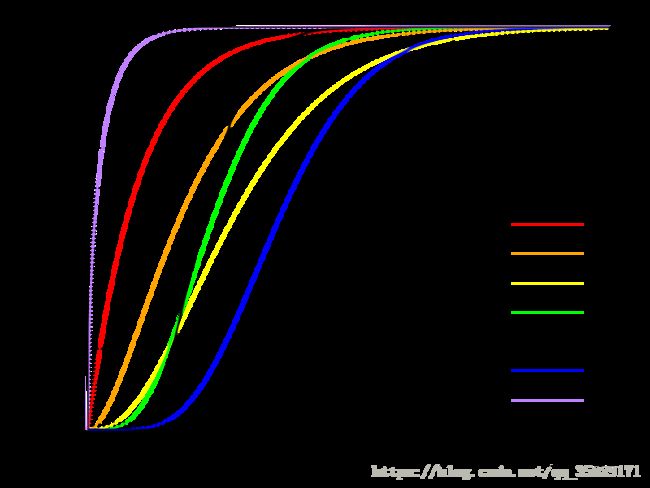
图形
Probability density function
Cumulative distribution function
parameters
Inv-Gamma分布
在通常情况下,同一物理量的多次测量数据都看成服从正态分布
N ( μ , σ 2 ) \N(\mu,\sigma^2)\ N(μ,σ2)
而当正态分布总体的均值 μ \mu μ已知时,其样本方差 σ 2 \sigma^2 σ2服从逆Gamma分布
I G ( σ 2 ; α , β ) IG(\sigma^2;\alpha,\beta) IG(σ2;α,β)
其中 α \alpha α, β \beta β为待求参数。由于逆Gamma分布具有共轭性,在使用Bayes统计决策方法时,其先验和后验分布密度具有相同的分布密度函数形式 I G ( σ 2 ; α , β ) IG(\sigma^2;\alpha,\beta) IG(σ2;α,β),因其使用方便,应用较广,尤其在测量数据的精度(方差)评估中使用的更加频繁。
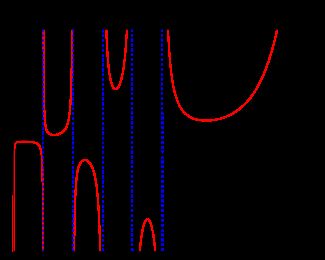
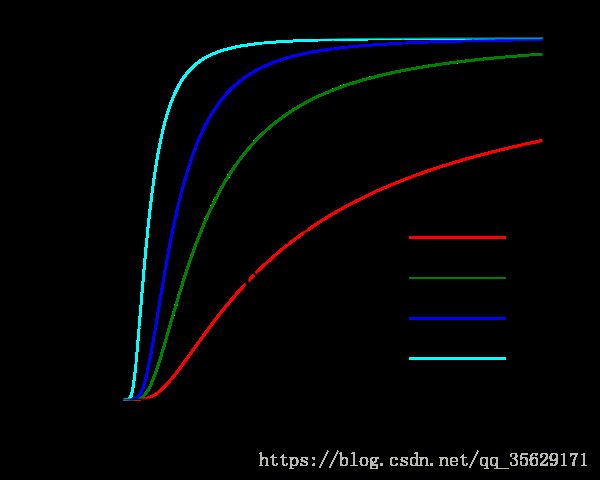
图形
Probability density function
Cumulative distribution function
parameters
Gamma分布与逆Gamma分布
若随机变量 X G a ( α , λ ) \ X~Ga(\alpha,\lambda) X Ga(α,λ), 则 1 X I G ( α , λ ) \frac{1}{X}~IG(\alpha,\lambda) X1 IG(α,λ)
图像python代码 1
Gamma 分布
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
fig=plt.figure(figsize=(18,6))#确定绘图区域尺寸
ax1=fig.add_subplot(1,2,1)#将绘图区域分成左右两块
ax2=fig.add_subplot(1,2,2)
x=np.arange(0.01,15,0.01)#生成数列
z1=st.gamma.pdf(x,0.9,scale=2)#gamma(0.9,2)密度函数对应值
z2=st.gamma.pdf(x,1,scale=2)
z3=st.gamma.pdf(x,2,scale=2)
ax1.plot(x,z1,label="a<1")
ax1.plot(x,z2,label="a=1")
ax1.plot(x,z3,label="a>1")
ax1.legend(loc='best')
ax1.set_xlabel('x')
ax1.set_ylabel('p(x)')
ax1.set_title("Gamma Distribution lamda=2")
y1=st.gamma.pdf(x,1.5,scale=2)#gamma(1.5,2)密度函数对应值
y2=st.gamma.pdf(x,2,scale=2)
y3=st.gamma.pdf(x,2.5,scale=2)
y4=st.gamma.pdf(x,3,scale=2)
ax2.plot(x,y1,label="a=1.5")
ax2.plot(x,y2,label="a=2")
ax2.plot(x,y3,label="a=2.5")
ax2.plot(x,y4,label="a=3")
ax2.set_xlabel('x')
ax2.set_ylabel('p(x)')
ax2.set_title("Gamma Distribution lamda=2")
ax2.legend(loc="best")
plt.show()
逆Gamma分布
from scipy.stats import invgamma
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 1)
a=[4,5,6]
for i in a:
mean, var, skew, kurt = invgamma.stats(i,scale=2,moments='mvsk')
x = np.linspace(invgamma.ppf(0.01,i,scale=2),invgamma.ppf(0.99,i,scale=2), 100)#invgamma.ppf
ax.plot(x, invgamma.pdf(x,i,scale=2,), label="a="+str(i))
ax.legend(loc="best")
ax.set_xlabel('x')
ax.set_ylabel('p(x)')
ax.set_title("Invgamma Distribution lamda=2")
plt.show()
https://blog.csdn.net/weixin_41875052/article/details/79843374 ↩︎