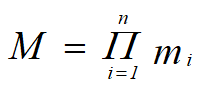数据库系统概论笔记———第二章 关系数据库

数据库系统概论笔记—第二章 关系数据库

本文参考的是中国人民大学王珊老师讲的数据库系统概论，整理自老师的PPT，如有问题请多指教。

2.1 关系数据结构及形式化定义

2.1.1 关系

• 单一的数据结构----关系
  现实世界的实体以及实体间的各种联系均用关系来表示
• 逻辑结构----二维表
  从用户角度，关系模型中数据的逻辑结构是一张二维表
• 建立在集合代数的基础上

域（Domain）

域是一组具有相同数据类型的值的集合。例:

• 整数
• 实数
• 介于某个取值范围的整数
• 指定长度的字符串集合
• {‘男’，‘女’}
• ………………

笛卡尔积（Cartesian Product）

笛卡尔积
给定一组域D1，D2，…，Dn，允许其中某些域是相同的。
D1，D2，…，Dn的笛卡尔积为：
D1×D2×…×Dn ＝
｛（d1，d2，…，dn）｜diDi，i＝1，2，…，n｝

• 所有域的所有取值的一个组合
• 不能重复

元组（Tuple）

• 笛卡尔积中每一个元素（d1，d2，…，dn）叫作一个n元组（n-tuple）或简称元组
• (张清玫，计算机专业，李勇)、(张清玫，计算机专业，刘晨) 等 都是元组

分量（Component）

• 笛卡尔积元素（d1，d2，…，dn）中的每一个值di 叫作一个分量
• 张清玫、计算机专业、李勇、刘晨等都是分量

基数（Cardinal number）

• 若Di（i＝1，2，…，n）为有限集，其基数为mi（i＝1，2，…，n），则D1×D2×…×Dn的基数M为：
  

笛卡尔积的表示方法

• 笛卡尔积可表示为一张二维表
• 表中的每行对应一个元组，表中的每列对应一个域

例

例如，给出3个域：

• D1=导师集合SUPERVISOR=｛张清玫，刘逸｝
• D2=专业集合SPECIALITY=｛计算机专业，信息专业｝
• D3=研究生集合POSTGRADUATE=｛李勇，刘晨，王敏｝

D1，D2，D3的笛卡尔积为
D1×D2×D3＝｛
(张清玫，计算机专业，李勇)，(张清玫，计算机专业，刘晨)，
(张清玫，计算机专业，王敏)，(张清玫，信息专业，李勇)，
(张清玫，信息专业，刘晨)，(张清玫，信息专业，王敏)，
(刘逸，计算机专业，李勇)，(刘逸，计算机专业，刘晨)，
(刘逸，计算机专业，王敏)，(刘逸，信息专业，李勇)，
(刘逸，信息专业，刘晨)，(刘逸，信息专业，王敏) ｝
基数为2×2×3＝12

关系（Relation）

（1） 关系
D1×D2×…×Dn的子集叫作在域D1，D2，…，Dn上的关系，表示为
                                                        R（D1，D2，…，Dn）

• R：关系名
• n：关系的目或度（Degree）

（2）元组
关系中的每个元素是关系中的元组，通常用t表示。

（3）单元关系与二元关系

当n=1时，称该关系为单元关系（Unary relation）或一元关系,
当n=2时，称该关系为二元关系（Binary relation）

（4）关系的表示
关系也是一个二维表，表的每行对应一个元组，表的每列对应一个域

（5）属性

• 关系中不同列可以对应相同的域
• 为了加以区分，必须对每列起一个名字，称为属性（Attribute）
• n目关系必有n个属性

（6）码

• 候选码（Candidate key）
  若关系中的某一属性组的值能唯一地标识一个元组，则称该属性组为候选码
  简单的情况：候选码只包含一个属性
• 全码（All-key）
  最极端的情况：关系模式的所有属性组是这个关系模式的候选码，称为全码（All-key）
• 主码
  若一个关系有多个候选码，则选定其中一个为主码（Primary key）
• 主属性
  候选码的诸属性称为主属性（Prime attribute）
  不包含在任何侯选码中的属性称为非主属性（Non-Prime attribute）或非码属性（Non-key attribute）
• D1，D2，…，Dn的笛卡尔积的某个子集才有实际含义
  例：表2.1 的笛卡尔积没有实际意义
  取出有实际意义的元组来构造关系
  关系：SAP(SUPERVISOR，SPECIALITY，POSTGRADUATE,)
  假设：导师与专业：n:1， 导师与研究生：1:n
  主码：POSTGRADUATE（假设研究生不会重名）
  
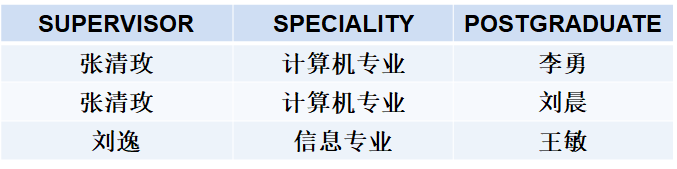
  （7）三类关系
  基本关系（基本表或基表）
          实际存在的表，是实际存储数据的逻辑表示
  查询表
          查询结果对应的表
  视图表
          由基本表或其他视图表导出的表，是虚表，不对应实际存储的数据

（8）基本关系的性质
① 列是同质的（Homogeneous）
② 不同的列可出自同一个域

• 其中的每一列称为一个属性
• 不同的属性要给予不同的属性名

③ 列的顺序无所谓,，列的次序可以任意交换
④ 任意两个元组的候选码不能相同
⑤ 行的顺序无所谓，行的次序可以任意交换
⑥ 分量必须取原子值
      这是规范条件中最基本的一条

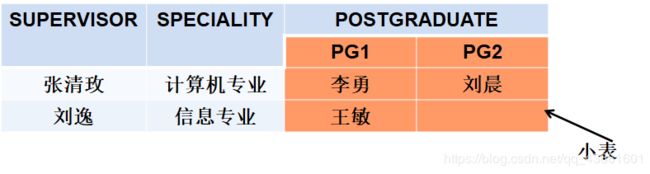
                                                                表2.3 非规范化关系

2.1.2 关系模式

1. 什么是关系模式

• 关系模式（Relation Schema）是型
• 关系是值
• 关系模式是对关系的描述
  • 元组集合的结构
    • 属性构成
    • 属性来自的域
    • 属性与域之间的映象关系
  • 完整性约束条件

2. 定义关系模式

关系模式可以形式化地表示为：
    R    （U，D，DOM，F）
    R    关系名
    U    组成该关系的属性名集合
    D    U中属性所来自的域
    DOM    属性向域的映象集合
    F    属性间数据的依赖关系的集合
例：
导师和研究生出自同一个域——人，取不同的属性名，并在模式中定义属性向域的映象，即说明它们分别出自哪个域：
DOM（SUPERVISOR-PERSON = DOM（POSTGRADUATE-PERSON）= PERSON

关系模式通常可以简记为
        R (U) 或 R (A1，A2，…，An)

• R: 关系名
• A1，A2，…，An : 属性名
• 注：域名及属性向域的映象常常直接说明为属性的类型、长度

3. 关系模式与关系

• 关系模式
  • 对关系的描述
  • 静态的、稳定的
• 关系
  • 关系模式在某一时刻的状态或内容
  • 动态的、随时间不断变化的
• 关系模式和关系往往笼统称为关系
  通过上下文加以区别

2.1.3 关系数据库

• 关系数据库
  • 在一个给定的应用领域中，所有关系的集合构成一个关系数据库
• 关系数据库的型与值
  • 关系数据库的型: 关系数据库模式，是对关系数据库的描述
  • 关系数据库的值: 关系模式在某一时刻对应的关系的集合，通常称为关系数据库

2.1.4 关系模型的存储结构

关系数据库的物理组织

• 有的关系数据库管理系统中一个表对应一个操作系统文件，将物理数据组织交给操作系统完成
• 有的关系数据库管理系统从操作系统那里申请若干个大的文件，自己划分文件空间，组织表、索引等存储结构，并进行存储管理

2.2 关系操作

2.2.1 基本的关系操作

• 常用的关系操作
  • 查询操作：选择、投影、连接、除、并、差、交、笛卡尔积
    • 选择、投影、并、差、笛卡尔基是5种基本操作
  • 数据更新：插入、删除、修改
• 关系操作的特点
  • 集合操作方式：操作的对象和结果都是集合，一次一集合的方式

2.2.2 关系数据库语言的分类

• 关系代数语言
  • 用对关系的运算来表达查询要求
  • 代表：ISBL
• 关系演算语言：用谓词来表达查询要求
  • 元组关系演算语言
    • 谓词变元的基本对象是元组变量
    • 代表：APLHA, QUEL
  • 域关系演算语言
    • 谓词变元的基本对象是域变量
    • 代表：QBE
• 具有关系代数和关系演算双重特点的语言
  • 代表：SQL（Structured Query Language）

2.3 关系的完整性

关系的三类完整性约束

• 实体完整性和参照完整性
  • 关系模型必须满足的完整性约束条件称为关系的两个不变性，应该由关系系统自动支持
• 用户定义的完整性
  • 应用领域需要遵循的约束条件，体现了具体领域中的语义约束

2.3.1 实体完整性

• 规则2.1 实体完整性规则（Entity Integrity）
  • 若属性A是基本关系R的主属性，则属性A不能取空值
  • 空值就是“不知道”或“不存在”或“无意义”的值
  • 例：
    选修（学号，课程号，成绩）
    “学号、课程号”为主码
    “学号”和“课程号”两个属性都不能取空值
• 实体完整性规则的说明
  （1）实体完整性规则是针对基本关系而言的。
  一个基本表通常对应现实世界的一个实体集。
  （2）现实世界中的实体是可区分的，即它们具有某种唯
  一性标识。
  （3）关系模型中以主码作为唯一性标识。
  （4）主码中的属性即主属性不能取空值。
  主属性取空值，就说明存在某个不可标识的实体，即存在不可区分的实体，这与第（2）点相矛盾，因此这个规则称为实体完整性

2.3.2 参照完整性

1. 关系间的引用

在关系模型中实体及实体间的联系都是用关系来描述的，自然存在着关系与关系间的引用。
[例2.1] 学生实体、专业实体
　学生（学号，姓名，性别，专业号，年龄）
　 专业（专业号，专业名）
　 学号是学生的主码，专业号是专业的主码。

• 学生关系引用了专业关系的主码“专业号”。
• 学生关系中的“专业号”值必须是确实存在的专业的专业号
  
  例[2.3] 学生实体及其内部的一对多联系
  学生（学号，姓名，性别，专业号，年龄，班长）
  
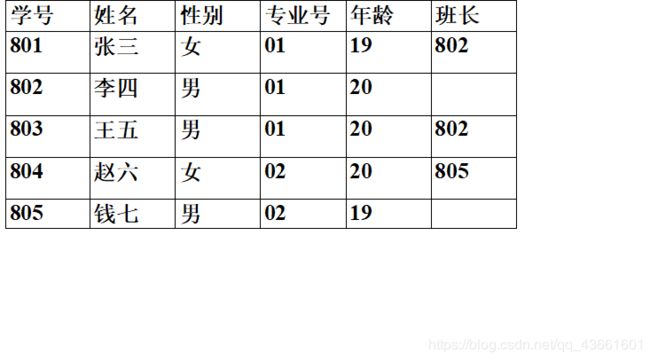
  “学号”是主码，“班长”是外码，它引用了本关系的“学号”
  “班长” 必须是确实存在的学生的学号

2. 外码

• 设F是基本关系R的一个或一组属性，但不是关系R的码。如果F与基本关系S的主码Ks相对应，则称F是R的外码
• 基本关系R称为参照关系（Referencing Relation）
• 基本关系S称为被参照关系（Referenced Relation）或目标关系（Target Relation）

[例2.1]中学生关系的“专业号”与专业关系的主码“专业号”相对应

• “专业号”属性是学生关系的外码
• 专业关系是被参照关系，学生关系为参照关系
  

[例2.2]中
选修关系的“学号” 与学生关系的主码“学号”相对应
选修关系的“课程号”与课程关系的主码“课程号”相对应

• “学号”和“课程号”是选修关系的外码
• 学生关系和课程关系均为被参照关系
• 选修关系为参照关系
  
  [例2.3]中“班长”与本身的主码“学号”相对应
• “班长”是外码
• 学生关系既是参照关系也是被参照关系
  
• 关系R和S不一定是不同的关系
• 目标关系S的主码Ks 和参照关系的外码F必须定义在同一个（或一组）域上
• 外码并不一定要与相应的主码同名
  当外码与相应的主码属于不同关系时，往往取相同的名字，以便于识别

3. 参照完整性规则

• 规则2.2 参照完整性规则
  若属性（或属性组）F是基本关系R的外码它与基本关系S的主码Ks相对应（基本关系R和S不一定是不同的关系），则对于R中每个元组在F上的值必须为：
  • 或者取空值（F的每个属性值均为空值）
  • 或者等于S中某个元组的主码值

[例2.1]中
学生关系中每个元组的专业号属性只取两类值：
（1）空值，表示尚未给该学生分配专业
（2）非空值，这时该值必须是专业关系中某个元组的“专业号”值，表示该学生不可能分配一个不存在的专业

[例2.2] 中
选修（学号，课程号，成绩）
“学号”和“课程号”可能的取值 ：
（1）选修关系中的主属性，不能取空值
（2）只能取相应被参照关系中已经存在的主码值

[例2.3] 中
学生（学号，姓名，性别，专业号，年龄，班长）
“班长”属性值可以取两类值：
（1）空值，表示该学生所在班级尚未选出班长
（2）非空值，该值必须是本关系中某个元组的学号值

2.3.3 用户定义的完整性

• 针对某一具体关系数据库的约束条件，反映某一具体应用所涉及的数据必须满足的语义要求
• 关系模型应提供定义和检验这类完整性的机制，以便用统一的系统的方法处理它们，而不需由应用程序承担这一功能

例:
课程（课程号，课程名，学分）

• “课程号”属性必须取唯一值
• 非主属性“课程名”也不能取空值
• “学分”属性只能取值{1，2，3，4}

2.4 关系代数

• 关系代数是一种抽象的查询语言，它用对关系的运算来表达查询
• 关系代数
  • 运算对象是关系
  • 运算结果亦为关系
  • 关系代数的运算符有两类：集合运算符和专门的关系运算符
• 传统的集合运算是从关系的“水平”方向即行的角度进行
• 专门的关系运算不仅涉及行而且涉及列
  

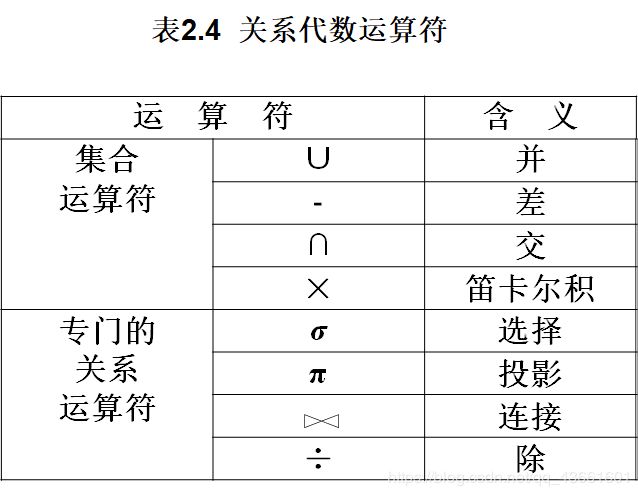
2.4.1 传统的集合运算

（1） 并（Union）

• R和S
  • 具有相同的目n（即两个关系都有n个属性）
  • 相应的属性取自同一个域
• R∪S
  • 仍为n目关系，由属于R或属于S的元组组成
                R∪S = { t|t ∈ R∨t ∈S }
    

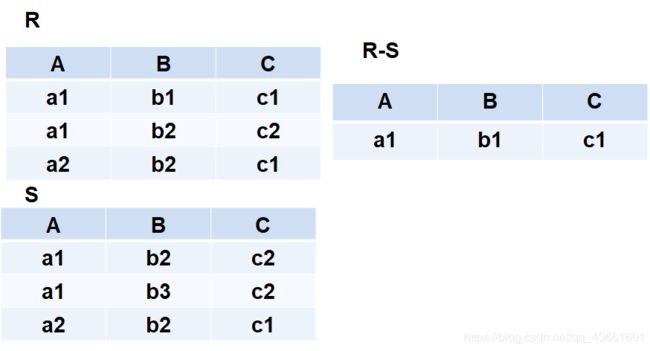
（2）差（Difference）

• R和S
  • 具有相同的目n
  • 相应的属性取自同一个域
• R - S
  • 仍为n目关系，由属于R而不属于S的所有元组组成
                R -S = { t|t∈R∧t∉S }
    

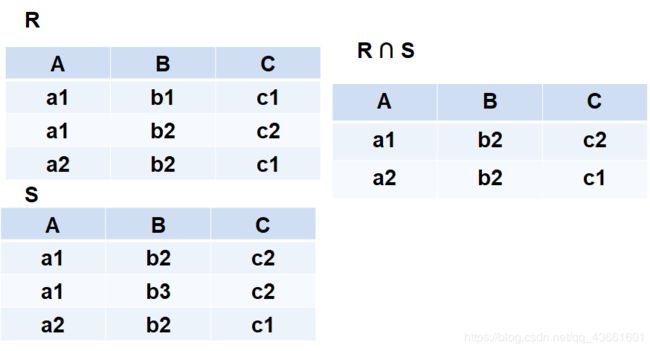
（3） 交（Intersection）

• R和S
  • 具有相同的目n
  • 相应的属性取自同一个域
• R∩S
  • 仍为n目关系，由既属于R又属于S的元组组成
                R∩S = { t|t ∈ R∧t ∈S }
                R∩S = R –(R-S）
    

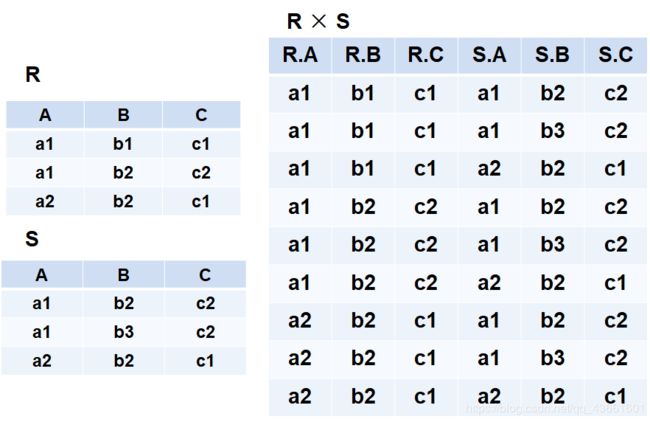
（4） 笛卡尔积（Cartesian Product）

• 严格地讲应该是广义的笛卡尔积（Extended Cartesian Product）
• R: n目关系，k₁个元组
• S: m目关系，k₂个元组
• R×S
  • 列：（n+m）列元组的集合
    • 元组的前n列是关系R的一个元组
    • 后m列是关系S的一个元组
  • 行：k₁×k₂个元组
    • R×S = {$\stackrel{⌢}{\mathrm{trts}}$|t_r ∈R ∧ t_s∈S }
      

2.4.2 专门的关系运算

先引入几个记号

（1） R，t∈R，t[A_i]
设关系模式为R(A1，A2，…，An)
它的一个关系设为R
t∈R表示t是R的一个元组
t[A_i] 则表示元组t中相应于属性Ai的一个分量

（2） A，t[A]， $\overline{A}$
若A={A_i1，A_i2，…，A_ik}，其中A_i1，A_i2，…，A_ik是A₁，A₂，…，A_n中的一部分，则A称为属性列或属性组。
t[A]=(t[A_i1]，t[A_i2]，…，t[Aik])表示元组t在属性列A上诸分量的集合。
$\overline{A}$则表示{A₁，A₂，…，A_n}中去掉{Ai1，Ai2，…，Aik}后剩余的属性组。

（3）$\stackrel{⌢}{\mathrm{trts}}$
R为n目关系，S为m目关系。
tr∈R，ts∈S，$\stackrel{⌢}{\mathrm{trts}}$称为元组的连接。
$\stackrel{⌢}{\mathrm{trts}}$是一个n + m列的元组，前n个分量为R中的一个n元组，后m个分量为S中的一个m元组。

（4）象集Z_x
给定一个关系R（X，Z），X和Z为属性组。
当t[X]=x时，x在R中的象集（Images Set）为：
Z_x={t[Z]|t∈R，t[X]=x}
它表示R中属性组X上值为x的诸元组在Z上分量的集合

• x1在R中的象集
  Zx1 ={Z1，Z2，Z3}，
• x2在R中的象集
  Zx2 ={Z2，Z3}，
• x3在R中的象集
  Zx3={Z1，Z3}
  
  
  

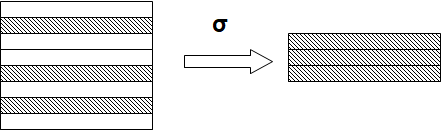
1. 选择

• 选择又称为限制（Restriction）
• 选择运算符的含义
  • 在关系R中选择满足给定条件的诸元组
    σ_F（R） = {t|t∈R∧F(t)= ‘真’}
  • F：选择条件，是一个逻辑表达式，取值为“真”或“假”
    • 基本形式为：X₁θY₁
    • θ表示比较运算符，它可以是＞，≥，＜，≤，＝或<>
• 选择运算是从关系R中选取使逻辑表达式F为真的元组，是从行的角度进行的运算
  
  
  

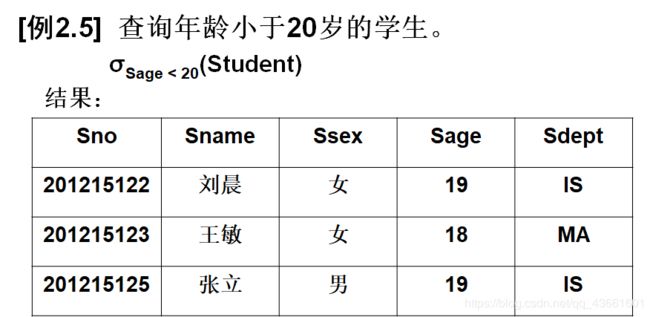
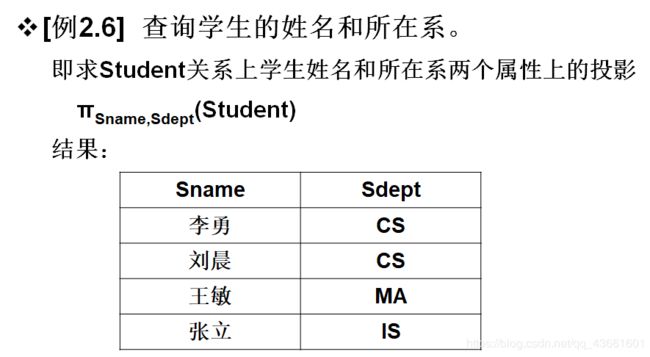
2. 投影

• 从R中选择出若干属性列组成新的关系
                          πA（R） = { t[A] | t ∈R }
                                                  A：R中的属性列
• 投影操作主要是从列的角度进行运算

• 投影之后不仅取消了原关系中的某些列，而且还可能取消某些元组（避免重复行）
  
  

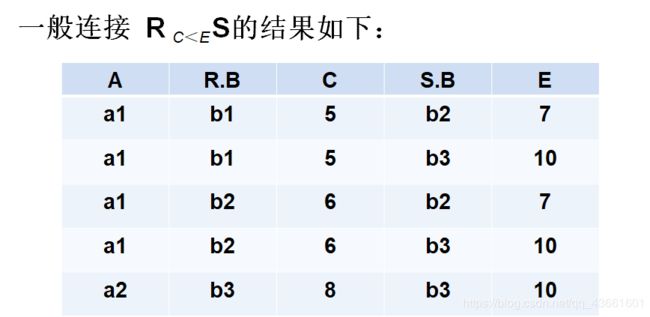
3. 连接

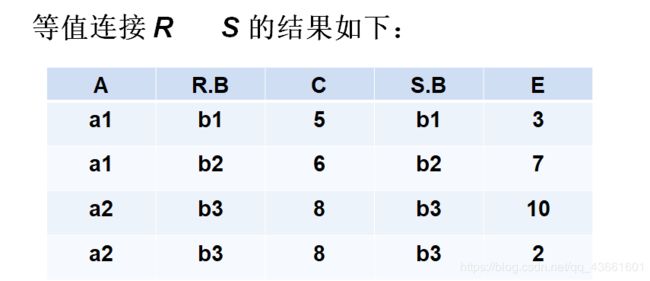
• 连接也称为θ连接
• 连接运算的含义
  从两个关系的笛卡尔积中选取属性间满足一定条件的元组
  
  • A和B：分别为R和S上度数相等且可比的属性组
  • θ：比较运算符
• 连接运算从R和S的广义笛卡尔积R×S中选取R关系在A属性组上的值与S关系在B属性组上的值满足比较关系θ的元组
• 两类常用连接运算
  • 等值连接（equijoin）
    • θ为“＝”的连接运算称为等值连接
    • 从关系R与S的广义笛卡尔积中选取A、B属性值相等的那些元组，即等值连接为：
      
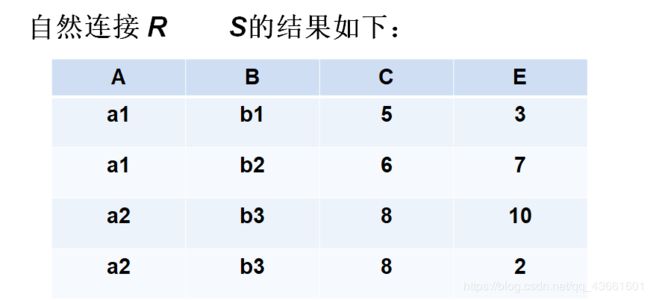
• 自然连接（Natural join）
  • 自然连接是一种特殊的等值连接
    • 两个关系中进行比较的分量必须是相同的属性组
    • 在结果中把重复的属性列去掉
  • 自然连接的含义
    R和S具有相同的属性组B
    
• 一般的连接操作是从行的角度进行运算。
  
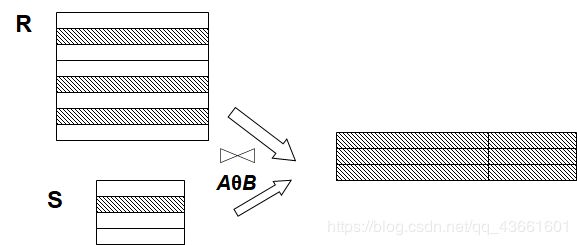
  自然连接还需要取消重复列，所以是同时从行和列的角度进行运算。

[例2.8]关系R和关系S 如下所示：

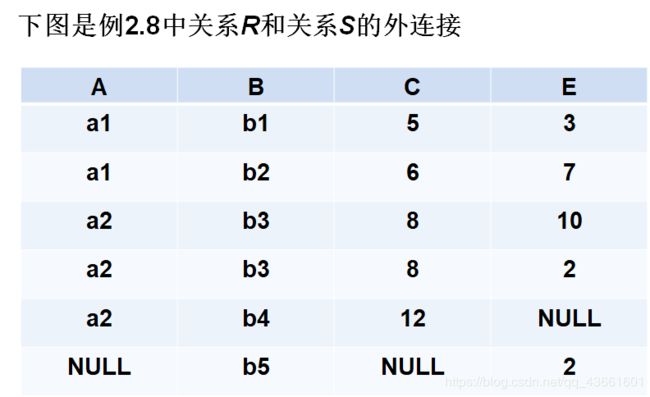
• 悬浮元组（Dangling tuple）
  • 两个关系R和S在做自然连接时，关系R中某些元组有可能在S中不存在公共属性上值相等的元组，从而造成R中这些元组在操作时被舍弃了，这些被舍弃的元组称为悬浮元组。
• 外连接（Outer Join）
  • 如果把悬浮元组也保存在结果关系中，而在其他属性上填空值(Null)，就叫做外连接
  • 左外连接(LEFT OUTER JOIN或LEFT JOIN)
    • 只保留左边关系R中的悬浮元组
  • 右外连接(RIGHT OUTER JOIN或RIGHT JOIN)
    • 只保留右边关系S中的悬浮元组
      
      

4. 除运算

给定关系R (X，Y) 和S (Y，Z)，其中X，Y，Z为属性组。
R中的Y与S中的Y可以有不同的属性名，但必须出自相同的域集。
R与S的除运算得到一个新的关系P(X)，
P是R中满足下列条件的元组在 X 属性列上的投影：
元组在X上分量值x的象集Yx包含S在Y上投影的集合，记作：
R÷S={t_r[X]|t_r∈R∧π_Y(S)⊆Y_x}
Y_x：x在R中的象集，x = t_r[X]


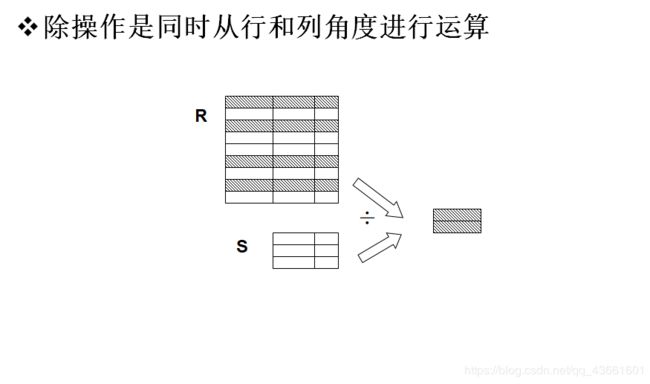
在关系R中，A可以取四个值{a1，a2，a3，a4}
a1的象集为 {(b1，c2)，(b2，c3)，(b2，c1)}
a2的象集为 {(b3，c7)，(b2，c3)}
a3的象集为 {(b4，c6)}
a4的象集为 {(b6，c6)}
S在(B，C)上的投影为
{(b1，c2)，(b2，c1)，(b2，c3) }
只有a1的象集包含了S在(B，C)属性组上的投影
所以 R÷S ={a1}

小结

• 关系代数运算
  • 关系代数运算
    • 并、差、交、笛卡尔积、投影、选择、连接、除
  • 基本运算
    • 并、差、笛卡尔积、投影、选择
  • 交、连接、除
    • 可以用5种基本运算来表达
    • 引进它们并不增加语言的能力，但可以简化表达
• 关系代数表达式
  • 关系代数运算经有限次复合后形成的式子
• 典型关系代数语言
  • ISBL（Information System Base Language）
    • 由IBM United Kingdom研究中心研制
    • 用于PRTV（Peterlee Relational Test Vehicle）实验系统

2.5 *关系演算

2.6 小结

• 关系数据库系统是目前使用最广泛的数据库系统
• 关系数据库系统与非关系数据库系统的区别：
  • 关系系统只有“表”这一种数据结构
  • 非关系数据库系统还有其他数据结构，以及对这些数据结构的操作
• 关系数据结构
  • 关系
    • 域
    • 笛卡尔积
    • 关系
      • 关系，属性，元组
      • 候选码，主码，主属性
      • 基本关系的性质
  • 关系模式
  • 关系数据库
  • 关系模型的存储结构
• 关系操作
  • 查询
    • 选择、投影、连接、除、并、交、差
  • 数据更新
    • 插入、删除、修改
• 关系的完整性约束
  • 实体完整性
  • 参照完整性
    • 外码
  • 用户定义的完整性
• 关系数据语言
  • 关系代数语言
  • 关系演算语言
    • 元组关系演算语言 ALPHA
    • 域关系演算语言 QBE