群体智能优化算法之萤火虫算法(Firefly Algorithm，FA)-看了还不会提刀来找我

获取更多资讯，赶快关注上面的公众号吧！

最近有小伙伴看到了我之前写的萤火虫算法相关的文章（ 群体智能优化算法之萤火虫算法(Firefly Algorithm，FA)），说是比较感兴趣，同时又有一些问题不太明白，所以今天我详细地再结合代码介绍一下这个算法，源码可以通过“ Github”获取。

22.1 萤火虫行为

萤火虫之间通过闪光来进行信息的交互，同时也能起到危险预警的作用。我们知道从光源到特定距离r处的光强服从平方反比定律，也就是说光强I随着距离 r 的增加会逐渐降低，即 $I\propto 1/r^2$，此外空气也会吸收部分光线，导致光线随着距离的增加而变得越来越弱。这两个因素同时起作用，因而大多数萤火虫只能在有限的距离内被其他萤火虫发现。

  萤火虫算法就是通过模拟萤火虫的发光行为而提出的，所以实际上其原理很简单。为了方便算法的描述，作者给出了三个理想化的假设：

• 所有萤火虫雌雄同体，以保证不管萤火虫性别如何，都能被其他萤火虫所吸引（每只萤火虫代表一个解，在实际问题中这和性别是没关系的，因此不必建模）；
• 吸引度与它们的亮度成正比，因此，对于任何两只闪烁的萤火虫，较暗的那只会朝着较亮的那只移动。吸引力与亮度程度会随着距离的增加而减小。最亮的萤火虫会随机选择方向进行移动（规定了解的更新方式，较暗移向较亮的可以认为是全局搜索，而最亮的进行随机移动属于局部搜索）；
• 萤火虫的亮度可受目标函数影响或决定，对于最大化问题，亮度可以简单地与目标函数值成正比（建立了算法与领域问题的关系，规定了如何将目标值表示亮度）。
  

22.2 亮度和吸引度

在萤火虫算法中，有两个重要的问题:光强的变化和吸引度的形成。为了简单起见，我们总是可以假设萤火虫的吸引度是由它的亮度决定的，而亮度又与目标函数相关。

  对于最大化优化问题，萤火虫在某一位置x的亮度I可以设定与目标函数 $f(\mathbf{x})$ 成正比，即 $I(\mathbf{x})\propto f(\mathbf{x})$。但是吸引度是相对的，它应该是由其他萤火虫所感受或断定的，因此该值会因萤火虫i和萤火虫j之间的距离 $r_{ij}$ 不同而不同，同光强一样，也会收到空气吸收程度的影响。光强I(r)的变化遵循平方反比定律 $I(r)=I_s/r^2$，$I_s$ 为光源处的强度。对于给定的具有固定光吸收系数 $\gamma$ 的介质（如空气），光强I与距离r有关，即 $I=I_0{e}^{-\gamma r}$，$I_0$ 为原始光强。为了避免 $I_s/r^2$ 在r=0 时除以 0，采用一种考虑平方反比律和吸收的综合近似表达方式：
$$I(r)=I_0{e}^{-\gamma r^2}\text{\hspace{1em}(1)}$$
如果希望函数单调递减的速度慢一点，则可以使用下式：
$$I(r)=\frac{I_0}{1+\gamma r^2}\text{\hspace{1em}(2)}$$
有了光强接下来就可以定义吸引度 $\beta$ 了，由于萤火虫的吸引度正比于光强，所以有：
$$\beta (r)={\beta }_0{e}^{-\gamma r^2}\text{\hspace{1em}(3)}$$
${\beta }_0$ 为r=0 处的吸引度。
在具体实现中，吸引度函数 $\beta (r)$ 可以是任意形式的单调递减函数：
$$\beta (r)={\beta }_0{e}^{-\gamma r^m},(m\ge 1)\text{\hspace{1em}(4)}$$

22.3 距离和移动

任意两只萤火虫i和j在其各自位置 ${\mathbf{X}}_i$ 和 ${\mathbf{X}}_j$ 上的距离为笛卡尔距离：
$$r_{ij}=\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert =\sqrt{\sum _{k=1}^d{\left(x_{i,k}-x_{j,k}\right)}^2}\text{\hspace{1em}(5)}$$
其中 $x_{i,k}$ 为第i只萤火虫空间坐标 ${\mathbf{X}}_i$ 的第k维坐标值。对于二维情况，$r_{ij}=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2}$。

  萤火虫i会向着比它更亮的其他萤火虫j的方向移动：
$${\mathbf{x}}_i={\mathbf{x}}_i+{\beta }_0{e}^{-\gamma r_{ij}^2}\left({\mathbf{x}}_j-{\mathbf{x}}_i\right)+\alpha \left(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}-\frac{1}{2}\right)\text{\hspace{1em}(6)}$$
式中第二项刻画了吸引度的作用，第三项为随机扰动项，$\alpha$ 为步长，rand 为[0,1]之间均匀分布的随机数。在绝大数应用中，可以设定 ${\beta }_0=1$,$\alpha \in [0,1]$,当然也可以设定随机项服从正太分布N(0,1)或其他分布。此外，如果数值范围在不同维度上相差很大，如在一个维度上范围为 $-10^5$ 到 $10^5$，另一个维度上范围为[-0.001,0.01]，需要首先根据领域问题的实际取值范围确定各个维度上的缩放系数 $S_k(k=1,\dots ,d)$，然后使用 $\alpha S_k$ 代替 $\alpha$。

22.4 算法和参数分析

总体来说萤火虫算法原理很简单，参数也不多，这也是其收敛速度快、性能稳定的原因。下面按照式（6）从左往右的顺序一一分析一下这些参数对算法的影响。

  ${\beta }_0$：初始吸引度，也就是自身对自身的吸引度，该值通常设为 1。为什么呢？我们先将随机项忽略，我们将式（6）整理以下，可以得到：
$${\mathbf{x}}_i=(1-{\beta }_0{e}^{-\gamma r_{ij}^2}){\mathbf{x}}_i+{\beta }_0{e}^{-\gamma r_{ij}^2}{\mathbf{x}}_j\text{\hspace{1em}(7)}$$
没有发现这个等式很熟悉吗？它实际上表达的就是在 ${\mathbf{X}}_i$ 和 ${\mathbf{X}}_j$ 连线上中间的一个点，设定 ${\beta }_0=1$，一方面如果 ${\mathbf{X}}_i$ 和 ${\mathbf{X}}_j$ 是同一个点，那么得到的新点仍为 ${\mathbf{X}}_i$，另一方面如果不是同一个点，那么将确保新点为两点之间连线上的点。

  $\gamma$：吸引度衰减参数，其取值范围为[0,+∞)。如果取 0，则吸引度为常量 $\beta ={\beta }_0$，这等于说光强不会随着距离衰减，那么萤火虫就可以被其他任意位置的萤火虫发现，所有的萤火虫都会朝着最亮的萤火虫靠近，从而很快收敛到一个最优值，这和只关注全局最优解的 PSO 有些类似；如果取值为+∞，那么 $\beta$ ->0，意味着在其他萤火虫眼中吸引度几乎为 0，那么萤火虫就是短视的，相当于，火虫是闭上眼睛随机移动的，这时进行的就是纯随机搜索。由于 $\beta$ 取值一般介于这两个极端之间（常取值为 $\gamma =1/\sqrt{L}$，L为领域问题各个维度的平均范围），因此常能得到比 PSO 和随机搜索更好的结果。

  $\alpha$：控制随机扰动的步长。该值不能太大，否则会导致算法出现震荡，无法收敛，也不能太小，否则无法进行有效的局部搜索。一般情况下，$\alpha =0.01L$。也可以设置自适应的 $\alpha$，通过迭代次数来更新其值：
$${\alpha }_t={\alpha }_0{\delta }^t,0<\delta <1)\text{\hspace{1em}(8)}$$
其中 ${\alpha }_0$ 为初始随机缩放因子，$\delta$ 为冷却因子，通常 ${\alpha }_0=0.01L$，$\delta$=0.95~0.97。

完整的 FA 算法如下图所示。

图1 FA伪代码

FA 算法有两个遍历种群n的内循环，一个迭代次数t的外循环，因此算法在最坏情况下复杂度为 $O\left(n^{2}t\right)$，由于n很小(通常为n = 40)，而t很大(比如t = 5000)，计算成本相对较低，因为算法复杂度与t呈线性关系，主要的计算成本将在目标函数的评估上。如果 n 相对较大，则可以使用一个内部循环，通过排序算法对所有萤火虫的吸引力或亮度进行排序。在这种情况下，FA 算法的复杂度为 $O(nt\log (n))$。

  那么为什么 FA 看起来简单却这么有效呢？ 首先，FA 是群体智能算法，因此它具备群体智能算法所有的优点；其次，FA 基于吸引度，吸引度随着距离增加而降低，所以如果两个萤火虫离的很远，较亮的萤火虫不会将较暗的萤火虫吸引过去，这导致了这样一个事实，即整个种群可以自动细分为子群体，每个子群体可以围绕每个模态或局部最优，在这些局部最优中可以找到全局最优解；最后，如果种群规模比模态数多得多，这种细分使萤火虫能够同时找到所有极值。

22.5 代码讲解

了解了以上算法原理后，下面基于 Java1.8 采用面向对象方法进行代码编码。完整代码可以点击“这里”查看， 包括 java 项目和算法原作者编写的 matlab 代码

  首先确定领域对象，包括萤火虫 Firefly、目标函数 ObjectiveFun、位置 Position 和范围 Range。

  其次实现算法类，由于 FA 存在多种改进版本，为了表示不同的算法内容，这里定义了算法接口，通过对其进行不同的实现建立不同的算法。

  最后针对具体优化问题进行了测试。

  下面结合代码具体说一下算法执行流程。

1. 初始参数设置。主要设置种群数量 popNum,最大迭代次数 maxGen，求解问题维度 dim，步长 alpha，初始吸引度 initAttraction，吸收因子 gamma，步长自适应 isAdaptive 和目标函数 objectiveFun 等。

// 新建目标函数
  ObjectiveFun objectiveFun = new ObjectiveFun();
  FANormal faNormal = FANormal.builder().popNum(40).maxGen(200).dim(2).alpha(0.2).initAttraction(1.0).gamma(1.0)
      .isAdaptive(true).objectiveFun(objectiveFun).build();
  faNormal.start();

2. 种群初始化。根据设定的种群大小，建立相应数量的萤火虫，在目标函数自变量的取值范围内随机确定每个萤火虫的位置；

@Override
public void initPop() {
  // TODO Auto-generated method stub
  System.out.println("**********种群初始化**********");
  fireflies = new ArrayList<>();
  for (int i = 0; i < popNum; i++) {
    fireflies.add(new Firefly(new Position(this.dim, objectiveFun.getRange())));
  }
}

3. 对初始种群进行亮度计算，即目标评估。对于最大化问题，评估过程中直接将目标作为亮度，对于最小化问题，则对目标值取相反数或倒数。之后再对萤火虫按照亮度进行排序，以确定当前种群中最优的个体。

@Override
public void calcuLight() {
  // TODO Auto-generated method stub
  for (Firefly firefly : fireflies) {
    firefly.setLight(this.getObjectiveFun().getObjValue((firefly.getPosition().getPositionCode())));
  }
  Collections.sort(fireflies);
  // 展示萤火虫分布
}

4. 萤火虫移动。亮度较低的萤火虫飞向亮度较高的萤火虫，亮度最亮的萤火虫随机移动。注意第 15 行计算了取值范围向量，这是针对多维空间优化问题时不同维度取值范围不同而设定的，对于取值范围较大的维度，在随机搜索时可以以较大的步长移动，而对于取值范围较小的维度，最好移动的不要太剧烈，所以通过该取值范围向量就可以很好的控制各个维度的变化量。

@Override
public void fireflyMove() {
  // TODO Auto-generated method stub
  for (int i = 0; i < popNum; i++) {
    for (int j = 0; j < popNum; j++) {
      Firefly fireflyi = fireflies.get(i);
      Firefly fireflyj = fireflies.get(j);
      if (i != j && fireflyj.getLight() > fireflyi.getLight()) { // 当萤火虫j的亮度大于萤火虫i的亮度时
        double[] codei = fireflyi.getPosition().getPositionCode();
        double[] codej = fireflyj.getPosition().getPositionCode();
        // 计算萤火虫之间的距离
        double disij = calcDistance(codei, codej);
        // 计算吸引度beta
        double attraction = initAttraction * Math.pow(Math.E, -gamma * disij * disij); // 计算萤火虫j对萤火虫i的吸引度
        double[] scale = fireflyi.getPosition().getRange().getScale();
        double[] newPositionCode = IntStream.range(0, this.dim).mapToDouble(ind -> codei[ind]
            + attraction * (codej[ind] - codei[ind]) + alpha * (random.nextDouble() - 0.5) * scale[ind])
            .toArray();
        fireflyi.getPosition().setPositionCode(newPositionCode);
      }
    }
  }
  // 对最亮的萤火虫进行随机移动
  Firefly bestFirefly = fireflies.get(popNum - 1);
  double[] scale = bestFirefly.getPosition().getRange().getScale();
  double[] newPositionCode = IntStream.range(0, dim).mapToDouble(
      i -> bestFirefly.getPosition().getPositionCode()[i] + alpha * (random.nextDouble() - 0.5) * scale[i])
      .toArray();
  bestFirefly.getPosition().setPositionCode(newPositionCode);
}

5. 更新迭代器。迭代次数加 1，同时如果设置了步长自适应，则步长进行进一步的缩放。

public void incrementIter() {
  iterator++;
  if (isAdaptive) {
    alpha *= delta;
  }
}

6. 循环。循环执行步骤 2~5，直到迭代次数达到设定的最大迭代次数。

while (this.iterator < maxGen) {
    calcuLight();
    fireflyMove();
    incrementIter();
    System.out.println("**********第" + iterator + "代最优解：" + fireflies.get(popNum - 1) + "**********");
  }

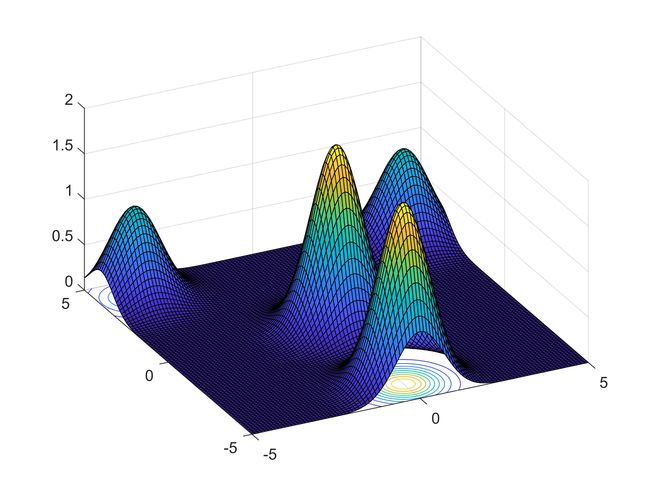
测试中使用的目标函数（最大化）方程和图像分别如下：

exp(-(x-4)^2-(y-4)^2)+exp(-(x+4)^2-(y-4)^2)+2*exp(-x^2-(y+4)^2)+2*exp(-x^2-y^2)

图2 目标函数三位曲面图

x、y 取值范围均为[-5,5],在此区间上该函数存在两个全局最优解(0,0)和(0,-4)，多次运行程序可得到这两个近似最优解。

图3 全局最优解(0,0)

图4 全局最优解(0,-4)

最后看一下萤火虫的是怎么移动的，通过图 5 可以看出，萤火虫形成了不同的子种群，各自收敛到一个局部最优解，这恰恰印证了之前关于 FA 有效性分析中的自动化分子种群的描述。

图5 萤火虫动态移动过程

22.6 FAQ 环节

Q1：步长为什么要减小，会不会影响收敛速度？

  A1：自适应步长 $\alpha$ 其实在算法参数那一部分已经介绍到了，那里我提到说 $\alpha$ 不能太大也不能太小，但实际上我们更希望步长在算法初期具有更大的探索性，而在算法后期需要收敛的时候应该使得算法更加稳定，我们才设计步长是不断自适应减小的，但是有一点值得注意，这个参数本质上和收敛速度关系不是很大，这个参数更多的是促进种群的多样性，因为步长是控制随机项的，随机越大，种群越多样，那么算法也就不太可能收敛。

  Q2:亮度重新赋值的目的？

  A2:说白了亮度就是目标函数值（最大化问题），所以在算法中萤火虫一旦进行了移动，就需要对其重新进行评估，要不怎么知道下一步往哪个更亮的方向移动呢？

  Q3：开源代码有吗？

  A3：点击“这里”查看 github 链接。

  Q4：在处理图像数据时是否也应该使用自适应步长？

  A4：自适应步长是针对算法而言的，和优化问题本身没关系，要说有关系那就是步长初始值的设定，通常领域问题不同，初始值设定就不同。

  Q5：算法原作者给出的 matlab 代码是否 OK？

  A5：这段代码思路上没啥问题，只不过是针对具体的优化问题而编写的，在解决自己的实际问题时，可能需要进行部分修改。