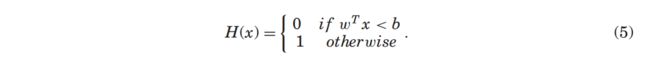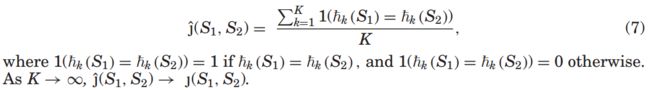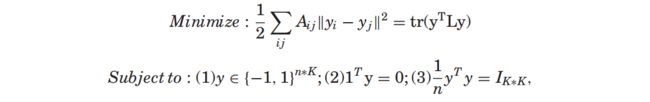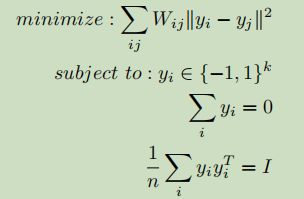图像检索哈希算法综述

本文主要参考自：Hashing Techniques: A Survey and Taxonomy

LIANHUA CHI, IBM Research, Melbourne, Australia
XINGQUAN ZHU, Florida Atlantic University, Boca Raton, FL; Fudan University, Shanghai, China

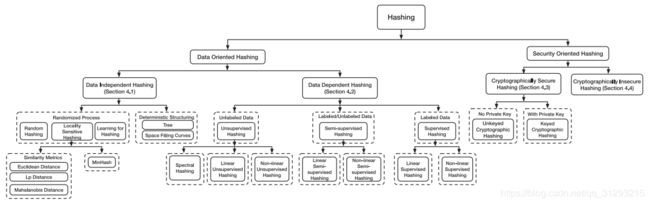
面向数据的主要为了加速查找过程，面向加密的主要为了产生验证签名

其中，本文关注面向数据部分：

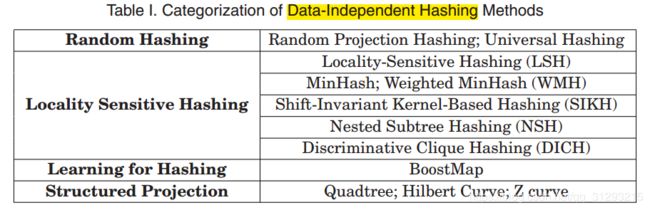
一、数据独立哈希：

没有训练过程，没有带标签的数据/信息。哈希函数都是prespecified，可以学习数据分布信息。可分四类：
随机哈希，局部敏感哈希，learning for hashing，结构投影

1.随机哈希

随机预测哈希有一个数据降维机制，可以自动把原始高维数据预测到低维空间。起初[Donald 1999]用随机的随机预测函数，一个随机预测函数需要d*lgk位来表示，d和k分别是原始数据和降维后数据的维度，导致无法存储随机选择函数，后来就开始用固定的随机预测函数，Carter and Wegman [1977]提出普遍方法，从特定函数的一个小集合中随机选哈希函数，如Shakhnarovich [2005]，随机函数预测的时间复杂度由于哈希函数簇小且高度独立，可以是常量级的。

主要缺点：太不稳定，不同的哈希函数会导致完全不同的编码，可能两个元素差一位，但哈希码可能被预测成不同的类别。在降维时也丢失了很多特性。随之产生了局部敏感哈希。

2.局部敏感哈希

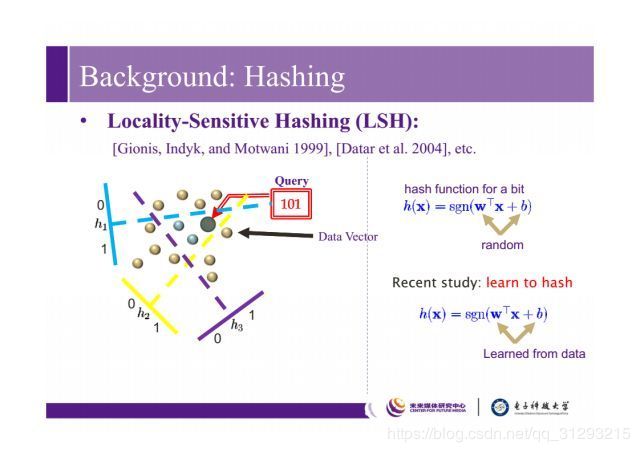
LSH的一大特点是原始空间相近的两个数据点哈希编码也相似。LSH的随机预测哈希函数是：

w是图像点的一个随机超平面，b是随机截距，每个数据点的标签由超平面w决定，LSH的哈希函数满足

基于这个哈希函数，对于任意两个点x,y，LSH满足

LSH不仅在哈希码中保留了数据特性，也保证相似数据点的碰撞可能性。

不足：效率低，且要保证精度需要很长的编码，low recall。

对于超平面，为了给出最优的编码位数，NPQ基于可适应的可学习的阈值分配，VBQ提供数据驱动的不一致位分配。

图源 http://www.sohu.com/a/217422745_610473

如上图左边所示，随机在空间里划几个超平面，就可以把数据分到不同空间里，比如中间这个小三角的区域就可以赋值为101，之前w，b是随机生成得到的，而现在更多是基于机器学习或者依赖于数据而得到的。

MinHash

独立的置换局部敏感哈希方法(min-wise independent permutations locality-sensitive hashing scheme)，用来针对两个集合迅速计算相似度。
对两个集合S1，S2应用K个哈希函数，S1，S2最小的哈希值是他们的MinHash，通过检查两个集合的最小哈希值就可以快速获得集合相似度，不需要复杂的集合元素计算。算法如下：

例子如下：

h1和h2是两个哈希函数（置换，permutations），S1：{1,2,4,7}，S2：{3,4,7}，h1：[2,5,7,6,4,3,1]，h2：[7,3,1,2,5,4,6]。应用h1到S1，第一个关联元素(h1S1交集元素)是2故h1(S1)=2，依次计算h1(S2)=7，h2(S1)=7，h2(S2)=7。再带入J(S1,S2)算得分子是1+0，分母K=2，所以相似度J(S1,S2)=1/2

Min-wise hashing可以检测搜索结果中相同的web页，几乎相似图片，大规模文档聚类，用Recursive Min-wise Hashing保留上下文信息，做大规模文本分类。

衍生：Weighted Minwise Hashing[Shrivastava 2016]更简单，快得多，存储效率高。

3.Learning for Hashing

数据敏感。

BoostMap[Shakhnarovich et al. 2006]

数据独立的机器学习方法，Euclidean embedding construction，BoostMap企图根据数据限定的每个任务学习一个新的embedding space，所以新的哈希空间最优地揭露了数据相似性。

先介绍几个基础的构建Euclidean embedding的方法：Lipschitz embedding[Johnson and Lindenstrauss 1984], Bourgain embedding [Hjaltason and Samet 2003;Bourgain 1985], FastMap [Faloutsos and Lin 1995], MetricMap [Wang et al. 2000] andBoostMap [Shakhnarovich et al. 2006]

Lipschitz embedding基本思想是低失真地嵌入度量空间到其他空间(embed metric spaces into other spaces with low distortion)，原始空间X的一个对象x转换到n维向量V=(v1,v2...vn)，每个元素vi对应 原始空间元素o和预定义的引用集合之间的距离 。表示原始空间中一维的Euclidean embedding P0。o叫做引用对象，如果Dx违背三角不等式(三角形任意两边和大于第三边)，原始空间中近邻的点就直观地通过P0映射到实线R上的近邻点，另一方面原始空间中离的远的点也可能映射到相近的点。

Bourgain embedding是Lipschitz embedding的特殊情况。

FastMap的基本思想是选择两个数据对象x1，x2作为pivot objects，然后定义任意x的embeddingPx1,x2作为x在x1x2线段上的预测。快速映射会分别根据x和x1以及x和x2距离预测。距离可以作为三角形的边处理

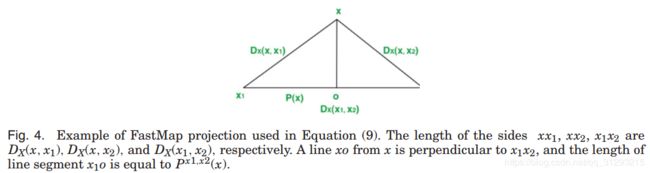Px1,x2预测数据，对于在原始空间中相近的能保留数据的相似结构，在FastMap中，多对pivot objects用来预测有限多的数据。

MetricMap扩展了FastMap，映射有限多个数据到伪欧式空间，使用非欧式空间时比FastMap效果好。

BoostMap优化了量化方法，和随机选择相比保留了更好的相似性排序，同时学习过程是独立的，不需要原始距离测量，核心是将embedding视为分类器以评估任意三个数据对象的距离，为了精度，使用AdaBoost整合所有的低位embedding到高维embedding。

BoostMap主要过程如下：

识别了大量的基于一对pivot objects或者一个引用对象的一维embeddings P，每个P视为连续的二进制分类器和弱分类器的输出。之后BoostMap使用AdaBoost结合一维embeddingP到多位embedding，得到比弱分类器精度高的强分类器。

4.结构投影

多数哈希函数都几乎只适用于低位数据，应用到高维或者超高维数据时效果可能下降。在High-Dimensional Vector Spaces(HDVSs)的相似性查找中，它使用传统方法--多维索引结构，这需要数据空间分割。很多方法是利用预定义的规则分割，无视数据的特征。Weber et al. [1998]证明了如果维度足够高，任何分区方案和聚类技术必须退化为对其所有块的顺序扫描。

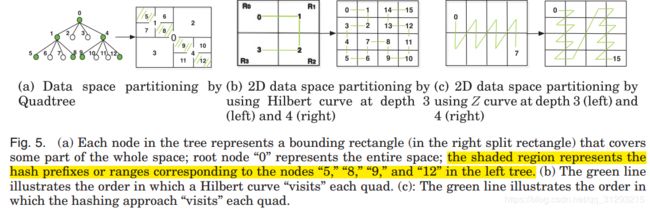
本文列举了一些树形结构来分割数据空间，结果也表明树形结构比顺序扫描效果好。比如四叉树常用来递归地将二维空间划分成四个部分。Joly et al. [2004] and Poullot et al. [2007]通过空间填充曲线投影研究基于内容的拷贝识别(studied the content-based copy identification by space-filling curve projection)，提出了一个巧妙策略：伪-不变特征识别，适用于基于内容的拷贝认证，采用Hilbert曲线作为投影线，直接映射一个Hilbert空间填充曲线的近似范围，以接近数据库。Hilbert曲线的优势是可以保证索引中的两个邻居数据在描述空间中还是邻居。

图5b展示了用Hilbert曲线分配二维数据空间。图5b左是2*2的基础Hilbert曲线，深度是3，Hilbert曲线复制了四部分R0R1R2R3，复制过程中R0顺时针翻转了90°，R3逆时针翻转了90°。旋转后两个lower quadrantsR0R3的功能反转了。两个upper quadrantsR1R2不会被旋转。如此我们可以获得深度是4的Hilbert曲线，只要在R0R3旋转和反转曲线就行了。

Hilbert曲线的缺点是很难从高维空间和高阶分区的描述空间中的位置开始计算索引中的键。键是cell在索引中的地址。

 

二、数据依赖哈希：

依靠训练数据学习哈希函数，由于数据依赖哈希对数据敏感，所以查询快占存小
为了更好保留局部信息，需要紧密耦合所给数据集的数据分布
分三类：无监督，半监督，监督
标签提供信息，可以实现实例间的语义分割，如果标签未知，可以用pairwise label弱(半)监督(对之间是否close)

1.无监督哈希

根据实际的哈希函数组成：包括特征函数，线性函数和非线性函数，我们将无监督哈希分如下三类：谱哈希，线性哈希和非线性哈希。

 

谱哈希[Weiss et al. 2009]

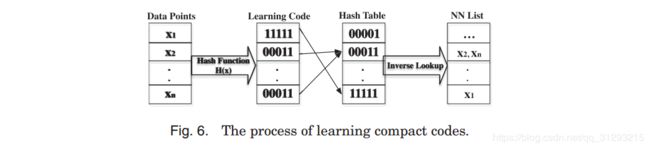
定义了优质编码的严格标准，和图分割有关。谱哈希的压缩编码过程入下：

​

图6：最左边是数据点，通过哈希函数H(x)，可以得到每个数据点对应的压缩编码，之后通过对哈希表的反向查找可以得到NNlist

谱哈希不只是在汉明空间保留样本的相似性，也找那些相似数据点间距最小的。

谱哈希假设输入数据在RD空间，输入空间中一对数据点(xi,xj)的相似度，越像越接近1，越不像越接近0。参数定义了RD中的距离，和相似项对应。相似邻居的平均汉明距离是，所以目标函数就是最小化汉明距离。

谱哈希满足如下标准(就是拉普拉斯特征映射加上三个约束)：

目标函数和约束的原文中的形式

其中L是图拉普拉斯矩阵 diag(A1)-A，约束2让编码平衡，约束3让位之间无关联。

注：目标函数(Laplacian Eigenmaps)推导如下(参考自https://blog.csdn.net/qrlhl/article/details/78066994)：

谱哈希需要训练，主要分三步：

1. 对原始数据应用PCA，对于一个确定的邻居图的n个数据点构建稀疏的相似度矩阵A。
2. 计算并二值化图拉普拉斯算子L的K个特征值最小的特征向量。
3. 一般化并二值化K个特征向量(以零为阈值划分二进制编码)，使其适应测试数据。

谱哈希在训练数据上做PCA，适应多维矩阵(multidimensional rectangle)，简单而高效。但训练过程在离线时很棘手，哈希过程又不能在线进行(But its training process is intractable for offline, and hashing process is infeasible for online)。

关于离散优化，在2015年之前，求解该问题基本分两步。第一步是将离散限制去掉，这就变成了连续优化的问题，可以用传统的梯度下降方法去求解，它的缺点是很难得到比较好的局部最优解；第一步去掉离散限制之后得到了连续的结果，第二步通过设定阈值进行二值化操作，比如将大于阈值的转为1，小于阈值的转为0，由此就得到了哈希码。当然，也可以利用类似2011年ITQ这篇工作去减少量化损失。这种方法的缺点是对于长哈希码（比如超过100比特），量化偏差会很大，使得学出来的哈希码不是很有效。后来以沈复民老师的SDH为代表等不再松弛离散约束，提出离散循环坐标下降法(DCC)直接优化离散编码。

哈希质量评价标准[Salakhutdinov and Hinton 2009]：

1. 对于新颖的输入也容易计算
2. 需要较少的位来编码完整的数据集
3. 相似的数据点编码也相似

缺点：位数增加时效果不好，通过欧氏距离对图拉普拉斯算子的构建可能不能反应数据的原始分布。虽然过成是直接计算训练数据，但是计算先前看不到的数据的哈希码是个问题。

为解决上述问题：Multidimensional Spectral Hashing (MSH) [Weiss et al. 2012]企图确保稳定性能，MSH希望重建数据点间的相似度，而不是用他们的距离。为了反映潜在的数据分布，Li et al. [2013]提出了一个基于图片/标签成对相似度的方法，直接优化图拉普拉斯算子，在优化过程中可以自动决定尺寸因素。为了计算先前看不到的数据点的哈希码，Bodo and Csat ´ o [2014]提出使用线性标量作为相似度测量，用不同的一般化(一个归纳生成公式)来计算哈希码，生成编码的方法和基于随机超平面的LSH一样。
 

2.线性无监督哈希

线性无监督哈希的哈希函数是线性函数，尽管有些是需要学习的。锚点图哈希AGH是代表性的，AGH会通过自动发掘数据中的邻居结构来学习合适的压缩编码。

AGH[Liu et al. 2011]

锚点图哈希应用锚点图来获得可用的，稀疏的，低秩的，非负的相似度矩阵。锚点图可以是K-means的聚类中心，当锚点数足够多时，一个锚点图可以刻画一个确定的邻居图。AGH首先计算数据to锚点的相似度Z(,n个数据点m个锚点)。基于Z计算数据to数据的相似度()，锚点to锚点的相似度是。如下图，红数据点是锚点，线是点间距离，数据to数据的是A矩阵，数据to锚点的是Z矩阵。

AGH的目标函数和约束是：

AGH主要分五步，123训练，45哈希：

1. 构建锚点图，获得数据to锚点的相似度矩阵Z
2. 计算并二值化锚点图拉普拉斯算子的K个特征向量
3. 构建哈希表
4. 将K个特征向量一般化到测试数据点上并二值化
5. 反转哈希表的查找