2020杭电HDU多校第一场Fibonacci Sum(斐波那契+二次剩余+玩命优化)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6755
Problem Description
The Fibonacci numbers are defined as below:
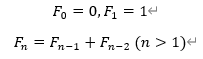
![]()
Given three integers N, C and K, calculate the following summation:
Since the answer can be huge, output it modulo 1000000009 (10^9+9).
Input
The first line contains an integer T (1≤T≤200), denoting the number of test cases. Each test case contains three space separated integers in the order: N, C, K (1≤N,C≤1018,1≤K≤105).
Output
For each test case, output a single line containing the answer.
Sample Input
2
5 1 1
2 1 2
Sample Output
12
2
emmm,比赛的时候随便都能水过去。。。赛后就疯狂T了。。。所以就要拼命优化代码了
博客园公式全部炸了,可能一篇白板了。。。。如果是加载不出来的话请到我的CSDN博客享用:
好吧,如果没有逛过我博客园的话我就放一下我的链接吧,目前只补了几个题QAQ
https://www.cnblogs.com/lonely-wind-/
首先我们讲讲它的做法吧。很显然,nc过于庞大,即使采用矩阵快速幂也是惘然的,那么我们只有在它的通项公式上做些手脚了,对于一个斐波那契数列,它的通项公式为(博客园公式编辑感觉炸了。。。怎么写都展示不了。。。只能放个图片了QAQ)
F ( n ) = 1 5 [ ( 1 + 5 2 ) n − ( 1 − 5 2 ) n ] F(n)=\frac{1}{\sqrt{5}} [(\frac{1+\sqrt{5}}{2})^{n} - (\frac{1-\sqrt{5}}{2})^{n}] F(n)=51[(21+5)n−(21−5)n]
虽然公式中含有根号,但是我们知道 F ( n ) F(n) F(n)是一个整数,而且5是模1e9+9的二次剩余,那么就可以通过逆元和二次剩余的转化来做比如根号5(公式又炸了这里改成文字了。。。)就可以用 x 2 ≡ 5 ( m o d 1 e 9 + 9 ) x^2\equiv 5(mod1e9+9) x2≡5(mod1e9+9)中的 x x x来代替。
以下为了方便我们将令
a = 1 + 5 2 a=\frac{1+\sqrt{5}}{2} a=21+5 b = a = 1 − 5 2 b=a=\frac{1-\sqrt{5}}{2} b=a=21−5 p = 5 p=\sqrt{5} p=5
那么式子就可以简化为 f n = 1 p ( a n − b n ) → f n c k = ( 1 p ) k ( a n c − b n c ) k f_n=\frac{1}{p}(a^n-b^n)\rightarrow f_{nc}^k=(\frac{1}{p})^k(a^{nc}-b^{nc})^k fn=p1(an−bn)→fnck=(p1)k(anc−bnc)k
那么将 ( a n c − b n c ) k (a^{nc}-b^{nc})^k (anc−bnc)k二项式展开就会得到:
C k 0 ( a n c ) k + C k 1 ( a n c ) k − 1 ( − b ) n c + ⋯ C k r ( a n c ) k − r ( ( − b ) n c ) r + ⋯ C_k^0(a^{nc})^k+C_k^1(a^{nc})^{k-1}(-b)^{nc}+\cdots C_k^r(a^{nc})^{k-r}((-b)^{nc})^r+\cdots Ck0(anc)k+Ck1(anc)k−1(−b)nc+⋯Ckr(anc)k−r((−b)nc)r+⋯
C k 0 ( a k ) n c + ( − 1 ) 1 C k 1 ( a k − 1 ) n c b n c + ⋯ ( − 1 ) r C k r ( a k − r ) n c ( b r ) n c + ⋯ C_k^0(a^k)^{nc}+(-1)^1C_k^1(a^{k-1})^{nc}b^{nc}+\cdots (-1)^rC_k^r(a^{k-r})^{nc}(b^{r})^{nc}+\cdots Ck0(ak)nc+(−1)1Ck1(ak−1)ncbnc+⋯(−1)rCkr(ak−r)nc(br)nc+⋯
那么他们的合式则有:
∑ i = 1 n ∑ r = 0 k ( − 1 ) r C k r ( a k − r ) i c ( b r ) i c → ∑ r = 0 k ∑ i = 1 n ( − 1 ) r C k r ( a k − r ) i c ( b r ) i c \sum_{i=1}^{n}\sum_{r=0}^{k}(-1)^rC_k^{r}(a^{k-r})^{ic}(b^r)^{ic}\rightarrow \sum_{r=0}^{k}\sum_{i=1}^{n}(-1)^rC_k^{r}(a^{k-r})^{ic}(b^r)^{ic} ∑i=1n∑r=0k(−1)rCkr(ak−r)ic(br)ic→∑r=0k∑i=1n(−1)rCkr(ak−r)ic(br)ic
那么继续变化则有
∑ r = 0 k ( − 1 ) r C k r ∑ i = 1 n ( a k − r ) i c ( b r ) i c → ∑ r = 0 k ( − 1 ) r C k r ∑ i = 1 n ( ( a k − r ) c ( b r ) c ) i \sum_{r=0}^{k}(-1)^rC_k^{r}\sum_{i=1}^{n}(a^{k-r})^{ic}(b^r)^{ic}\rightarrow \sum_{r=0}^{k}(-1)^rC_k^{r}\sum_{i=1}^{n}((a^{k-r})^{c}(b^r)^{c})^i ∑r=0k(−1)rCkr∑i=1n(ak−r)ic(br)ic→∑r=0k(−1)rCkr∑i=1n((ak−r)c(br)c)i
我们令 t = ( a k − r ) ( b r ) t=(a^{k-r})(b^r) t=(ak−r)(br)
那么式子可简化为 ∑ r = 0 k ( − 1 ) r C k r ∑ i = 1 n ( t c ) i \sum_{r=0}^{k}(-1)^rC_k^{r}\sum_{i=1}^{n}(t^c)^i ∑r=0k(−1)rCkr∑i=1n(tc)i里面是个等比数列求和,其公比为 t c t^c tc
那么于是此题便结束了。。。。(真的吗)
这里给出一个看似已经OK的代码:
#include 这个就会T了。。。。T飞了。。。
现在我们要考虑优化了,我们考虑优化掉几个快速幂,对于组合数,我们可以考虑用预处理分母中每个阶乘的逆元来代替在循环中的快速幂,即:
fac[0]=1;
for (int i=1; i<mac; i++)
fac[i]=(ll)fac[i-1]*i%mod;
fac_inv[1]=1,fac_inv[0]=1;
for (int i=2; i<mac-5; i++) fac_inv[i]=qpow(fac[i],mod-2);
那么对于组合数 C k r C_k^r Ckr的计算就可以直接一句话带走了:
int C=(ll)fac[k]*fac_inv[k-r]%mod*fac_inv[r]%mod;
OK,已经优化掉一个快速幂了,我们尝试着交一发(当然里面的long long全部都改成了int,必要的时候强转long long)。。。还是T了。
我们继续优化快速幂,我们看 t = t c t=t^c t=tc这个东西,实际上他是可以推过来的。我们观察一下前两个t:
t 0 c = ( a k ) c , t 1 c = ( a k − 1 b ) c t_0^c=(a^k)^c,t_1^c=(a^{k-1}b)^c t0c=(ak)c,t1c=(ak−1b)c
也就是说 t t t的变化是每次乘以b再除以a再c次方,即 t i c = t i − 1 c × ( b × i n v ( a ) ) c t_i^c=t_{i-1}^c\times (b\times inv(a))^c tic=ti−1c×(b×inv(a))c,那么每个公比 t c t^c tc的计算就可以变成:
int q=(ll)A[k]*B[0]%mod;
q=qpow(q,c);//公比
int tui=qpow((ll)de*qpow(ad,mod-2)%mod,c);//公比每次要乘的数,(b/a)^c
for (r,0,k) {
int tmp=(ll)q*(qpow(q,n)-1+mod)%mod*qpow(q-1,mod-2)%mod;
q=(ll)q*tui%mod;
}
于是我们再次优化掉一个快速幂_
交一发。。。。还是T的。。。(实际上我们做个欧拉降幂的话优化到这里就可以过了,只不过要跑1800ms+)
然后我们考虑,既然我们将公比 t c t^c tc优化掉了,那么 ( t c ) n (t^c)^n (tc)n应该可以优化掉的。
于是,这里就没了。为了方便令 s = ( t c ) n s=(t^c)^n s=(tc)n,那么刚开始的时候, s = q n s=q^n s=qn,然后怎么递推呢,实际上就是每次乘上 t u i n tui^n tuin就行了。最终就变成了如下版本:
int q=(ll)A[k]*B[0]%mod;
q=qpow(q,c);//公比
int tui=qpow((ll)de*qpow(ad,mod-2)%mod,c);//公比每次要乘的数,(b/a)^c
int fz=qpow(q,n);//递推t^c((t^c)^n)
int tui_fz=qpow(tui,n);
for (r,0,k) {
int C=(ll)fac[k]*fac_inv[k-r]%mod*fac_inv[r]%mod;
int tmp=(ll)q*(fz-1+mod)%mod*qpow(q-1,mod-2)%mod;
q=(ll)q*tui%mod;
fz=(ll)fz*tui_fz%mod;
}
再交一发。。。。emmm,A了,800ms+
以下是AC代码:
#include