Python与机器学习实战——SVM(1)

SVM
感知器能将线性可分数据集准确分割开，但是从损失函数可以看出，只是分割开了，但是没有一个最优解，比如：

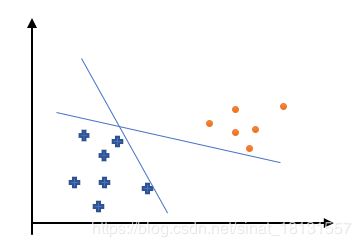
这样虽然两条直线都将数据集分开了，但是如果出现了一个新的数据点，很有可能这个数据点的分割结果是错误的。比如这样：

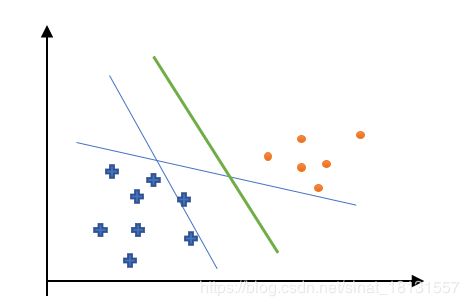
那么就需要绿色的这个“超平面”作为分类输出才行。这个最有“超平面”就是支持向量机SVM的分类思想。

线性SVM

在感知器中有描述到样本点$(x_i,y_i)$到超平面$\Pi ：w\cdot x+b=0$的相对距离为：
$$d^{\ast }(x_i,\Pi )=|w\cdot x_i+b|$$这个也被称为函数间隔（Functional Margin）,当$w$和$b$等比例变大变小时候，超平面不会发生变化，但是$d^{\ast }$却在变大变小，为了解决这个问题，引出了几何间隔（Geometric Margin）:
$$d(x_i,\Pi )=\frac{1}{||w||}|w\cdot x_i+b|=\frac{1}{||w||}{d}^{\ast }(x_i,\Pi )$$其中，$||w||$是$w$的欧式范数。SVM是让超平面到点集的距离最大化，也就是需要最大化几个间隔$d(x_i,\Pi )$,使得：
$$\frac{1}{||w||}(w\cdot x_i+b)y_i⩾d(i=1,..,N)$$这里，由于在超平面两边的样本点分别分别计算$w\cdot x_i+b$是有正有负的，而$y_i\in \{-1,+1\}$,所以能使得$(w\cdot x_i+b)y_i$都是正数。$y_i$在这个表示的是符号。
由于$d^{\ast }=||w||d$,所以上式两边同时乘以$||w||$，问题等价为最大化$d=\frac{d^{\ast }}{||w||}$,并使得：
$$(w\cdot x_i+b)y_i⩾d^{\ast }(i=1,..,N)$$可以发现$d\ast$的取值对优化问题的解（超平面的位置）没有影响，比如，当$d^{\ast }$变成了$\lambda d^{\ast }$,那么$w$和$b$也变成了$\lambda w$和$\lambda b$,但是超平面并没有变化。不妨假设$d^{\ast }=1$,问题转化为了最大化$\frac{1}{||w||}$使得：
$$(w\cdot x_i+b)y_i⩾1(i=1,..,N)$$由于$\frac{1}{||w||}$是非负的，最大化$\frac{1}{||w||}$，就是要最小化$||w||$,为了方便数学表达和计算，将优化问题写成最小化$\frac{1}{2}||w|{|}^2$使得：
$$(w\cdot x_i+b)y_i⩾1(i=1,..,N)$$这就是SVM最原始的形式，如果数据集D是线性可分的，那么SVM的解就存在且唯一。

假设最优化的解为$w^{\ast }$和$b^{\ast }$,那么称超平面：
$${\Pi }^{\ast }:w^{\ast }\cdot x+b^{\ast }=0$$为最大硬间隔分离超平面。考虑到不等式的约束条件可以知道在两个平面：
$$\begin{gathered} {\Pi }_1^{\ast }:w^{\ast }\cdot x+b^{\ast }=-1 \\ {\Pi }_2^{\ast }:w^{\ast }\cdot x+b^{\ast }=+1 \end{gathered}$$中间是没有点的，因为$(w\cdot x_i+b)y_i<1$了，但是在${\Pi }_1^{\ast }$和${\Pi }_2^{\ast }$上是有样本点的，通常称${\Pi }_1^{\ast }$和${\Pi }_2^{\ast }$为间隔边界，而边界上的点就是支持向量。

那么对于线性不可分的数据集呢？无法找到超平面完全分割数据集，更不用说要间隔最大化。就需要做出一定妥协，将“硬”间隔转化为“软”间隔，就是将不等式的条件放宽。
$$(w\cdot x_i+b)y_i⩾1\to (w\cdot x_i+b)y_i⩾1-{\xi }_i$$其中，${\xi }_i$被称为松弛变量，不小于0。加入这个松弛变量后，损失函数需要加入一个惩罚项：
$$\mathbf{L}(w,b,x,y)=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i$$C被称为惩罚因子，C越大，最终SVM的模型越不能容忍误分类的点，反之越小。
到现在，SVM算法的最优化问题变为了最小化$\mathbf{L}(w,b,x,y)$,并使得：
$$(w\cdot x_i+b)y_i⩾1-{\xi }_i(i=1,..,N)$$其中${\xi }_i⩾0$,所以可以定义：
$${\xi }_i=l(w,b,x,y)=\max (0,1-y(w\cdot x+b))$$其中$y\in \{-1,+1\}$,所以当模型判断不正确时候，就会有惩罚，而判断正确了就没有惩罚了。损失函数可以写为：
$$\mathbf{L}(w,b,x,y)=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^{N}l(w,b,x_i,y_i)$$同样也是使用梯度下降法进行训练的，所以有偏导数：
$$\begin{array}{c}\frac{\partial L(w,b,x,y)}{\partial w}=w+\{\begin{array}{l}0,y_i(w{x}_i+b)⩾1\\ -C{y}_i{x}_i,y_i(w{x}_i+b)<1\end{array}\\ \frac{\partial L(w,b,x,y)}{\partial b}=\{\begin{array}{l}0,y_i(w{x}_i+b)⩾1\\ -C{y}_i,y_i(w{x}_i+b)<1\end{array}\end{array}$$这样就可以写出线性SVM的算法实现过程：
输入：训练集$D=\{(x_1,y_1),...,(x_n,y_n)\}$，迭代次数M,学习率$\alpha$,其中：$$x_i\in \mathbf{X}\subseteq {\mathbb{R}}^n,y_i\in \{-1,+1\}$$过程：
(1)初始化参数：$$w=(0,...,0{)}^T\in {\mathbb{R}}^{\mathbb{N}},b=0$$(2)对$j=1,...,M$:
（a）算出误差向量$e=(e_1,...,e_n{)}^T$,其中：
$$e_i=1-y_i(w\cdot x_i+b)$$（b）取出误差最大的一项：
$$i=\underset{i}{\mathrm{argmax}}{e}_i$$（c）若$e_i⩽0$则退出循环。否则取对应样本来进行随机梯度下降：
$$\begin{gathered} w\leftarrow (1-\alpha )w+\alpha C{y}_i{x}_i \\ b\leftarrow b+\alpha C{y}_i \end{gathered}$$输出：线性SVM模型$g(x)=sign(f(x))=sign(w\cdot x+b)$

SVM算法的对偶形式

SVM的问题为：
$$\underset{w,b}{\min }L(w,b,x,y)=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i$$使得：
$$y_i(w\cdot x_i+b)⩾1-{\xi }_i$$其中：${\xi }_i⩾0$。那么原始问题的拉格朗日函数可以表达为(这里的$\alpha$不是学习率)：
$$L(w,b,\xi ,\alpha ,\beta )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i[y_i(w\cdot x_i+b)-1+{\xi }_i]-\sum _{i=1}^N{\beta }_i{\xi }_i$$为求解L的极小值，需要对$\alpha ,\beta ,\xi$求偏倒，并令为0。就有：
$$\begin{gathered} {\nabla }_{w}L=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0 \\ {\nabla }_{b}L=-\sum _{i=1}^N{\alpha }_i{y}_i=0 \\ {\nabla }_{{\xi }_i}L=C-{\alpha }_i-{\beta }_i \end{gathered}$$解得：
$$\begin{gathered} w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i \\ \sum _{i=1}^N{\alpha }_i{y}_i=0 \end{gathered}$$以及对$j=1,...,N$都有：
$${\alpha }_i+{\beta }_i=C$$带入计算可以得到拉格朗日函数为：
$$L(w,b,\xi ,\alpha ,\beta )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\alpha }_i$$所以原始函数的对偶问题就是求上式的最大值：
$$\underset{\alpha }{\max }(-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\alpha }_i)$$约束条件为
$$\sum _{i=1}^N{\alpha }_i{y}_i=0$$以及对$j=1,...,N$都有：
$$\begin{gathered} {\alpha }_i⩾0 \\ {\beta }_i⩾0 \\ {\alpha }_i+{\beta }_i=C \end{gathered}$$由于和是常数，所以上述约束条件可以简化为：
$$0⩽{\alpha }_i⩽C$$假设对偶形式的解为:${\alpha }^{\ast }=({\alpha }_1,...,{\alpha }_N{)}^T$,那么：
$$\begin{gathered} w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i \\ {b}^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j) \end{gathered}$$其中$b^{\ast }$中出现的$j$是满足$0⩽{\alpha }_i⩽C$的下标。