Python数据结构和算法(五):回溯真没你想的那么难(十道leetcode真题带你跨过这个坑)!
文章目录
- 前文
- 回溯算法定义和应用题型
- 回溯算法定义
- 回溯算法应用题型
- 回溯算法题型讲解
- combination sum系列
- 39. Combination Sum
- 40. Combination Sum II
- 216. Combination Sum III
- subsets系列
- 78. Subsets
- 90. Subsets II
- 79. Word Search
- Unique Paths系列
- 62. Unique Paths
- 63. Unique Paths II
- 64. Minimum Path Sum
- 120. Triangle
- 总结
前文
贪心、分治、回溯、动态并称为最经典最易考的四大算法,其中以贪心、分治易理解,回溯、动态相对难理解,前两者光听概念就能明白其大致实现,贪心即永远取当前最好的结果,比如有一个列表:[7,1,5,3,6,4],每个数字代表着货物的价值,从前往后开始,可以任意的购买和出售货物,但是同一天仅支持一个操作,问如何才能获取最大收益。这道题光是理解并用人脑来思考可能就会懵逼,但是只要用上贪心算法,那就非常简单。我不需要知道前几天是否买,然后后面统一卖;也不需要知道是否前天买后天卖是最划算的,只要知道一点,如果有利益我就购买和出售! 所以转换为实现,即后一天的货物价值比前一天高,那就买入前一天,出售后一天的即可!这道题对应着leetcode的:https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/。对应代码如下:
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
res = 0
for i,v in enumerate(prices[1:],1):
if v > prices[i-1]:
res += v - prices[i-1]
return res
可以看到非常简单,而分治原理也是很好理解,那就是分而治之!最典型的就是分布式算法,单台主机不够,那就加多台;单个任务过大,那就拆分成多个任务!而代码里我们比较熟悉的就是归并排序,将排序的复杂度永远的固定在O(NlogN),没有所谓的最好、最坏、均摊等等,如果想要归并排序代码,可以看我这篇文章:Python数据结构和算法(一):基于内存的五大排序算法!
回到主题,本篇主要讲回溯,而实际上回溯、动态基本归为一家,后者的复杂度要优于前者(大部分情况),不过本篇先讲回溯,下一篇再聊聊动态规划。
回溯算法定义和应用题型
回溯算法定义
回溯算法顾名思义就是不断回溯,而回溯的前提就是暴力枚举。也就是将所有的情况都罗列出来,然后通过不断尝试,得到最后的解,举个例子就是在迷宫里,每到一个分叉口,就将那个分叉口的路走遍,然后回到第二个分叉,继续走遍,直到将每条路都走遍,一旦发现不合适,就回溯到上个路口继续往下走。
回溯算法本质是依赖于递归,所以一定要把握好其基线条件,一旦确定了基线条件和递归方程,实现起来就非常轻松!另外在大多数题,我们可以利用”备忘录“来加快答案的得出,这个下文再分析。
适合回溯的经典有很多:八皇后、旅行商问题、01背包问题、数独、正则表达式等等,这些回头再说,本篇通过leetcode部分真题,详细记录这些套路。
回溯算法应用题型
经典题型以下两种最多:
- 迷宫类型:找出从入口到出口的所有解决方案、找出二维数组里左上角到右下角的所有方案等等
- 找子集合类型:给定一个数组,找出所有符合条件的子集合
除了以上的,剩下的比如斐波那契数列、01背包、八皇后等等也是leetcode的重要题型,这里重点介绍上述两类,10道题型看目录就行了,这边就不一一汇整。
回溯算法题型讲解
combination sum系列
这个系列属于找子集合类型,即给定一个数组,找出其中所有满足和为target的集合,让我们直接来看:
39. Combination Sum

题意是给定不重复的值,所以我们可以从第一个数开始,依次往下遍历,当遍历数之和小于target,就继续遍历,直到和为target就return。所以基线条件有两个:和=target,和>target。
举例说明,从2开始,往下遍历到2,发现和为4,然后继续往下遍历到3,发现和为7,此时达到基线条件,所以这个[2,2,3]加到队列里。同时回溯到6,发现[2,2,6]大于target,再次回溯,并以此类推。所以代码为:
class Solution:
def combination_sum(self,candidates,target):
self.res = []
self.dfs(0,candidates,target,[])
return self.res
#传入序号来标识每次遍历的起点,path来记录每次符合的结果集
def dfs(self,index,nums,target,path):
if target < 0: return
if target == 0:
self.res.append(path)
for i in range(index,len(nums)):#因为同一个值可用两次,所以序号要保持不变地开始下次遍历
self.dfs(i,nums,target-nums[i],path+[nums[i]])
40. Combination Sum II

比起上一道,这道题加了可重复,而且返回的结果集同一个值不能用两次,整体复杂了点,但大体思路是一致的。为了对付可重复,我们需要先排序,这样当遍历的时候发现前后两个数一样可以跳过;为了对付同一个值不能用两次,每次遍历的时候都要将序号+1,看代码就很清晰了:
class Solution2:
def combination_sum2(self,candidates,target):
self.res = []
candidates.sort()
self.dfs(0,candidates,target,[])
return self.res
def dfs(self,index,candidates,target,path):
if target == 0:
self.res.append(path)
return
if target < 0:return
for i in range(index,len(candidates)):
#增加判断是否是重复值,是的话直接跳过!
if i > index and candidates[i] == candidates[i - 1]:
continue
#这里要注意序号+1,防止同一个值用两次
self.dfs(i+1,candidates,target-candidates[i],path+[candidates[i]])
216. Combination Sum III

区别于前两题,增加了一个结果集要满足个数为k个数,而且是同一个值不可用多次,所以增加了一个限制k,所以基线条件的判断要加入k,但本质的解题方式是一致的:
class Solution3:
def combination_sum3(self,k,n):
self.res = []
self.dfs(1,k,n,[])
return self.res
def dfs(self,index,k,n,path):
if k < 0 or n <0: #增加k的判断
return
if n==0 and k==0: #增加k的判断
self.res.append(path)
return
for i in range(index,10):#这里是和combinationsum2的解法一致
self.dfs(i+1,k-1,n-i,path+[i])
subsets系列
同属于找子集合系列,subsets则直接粗暴的多,而他们的核心都是一样的,即:
78. Subsets
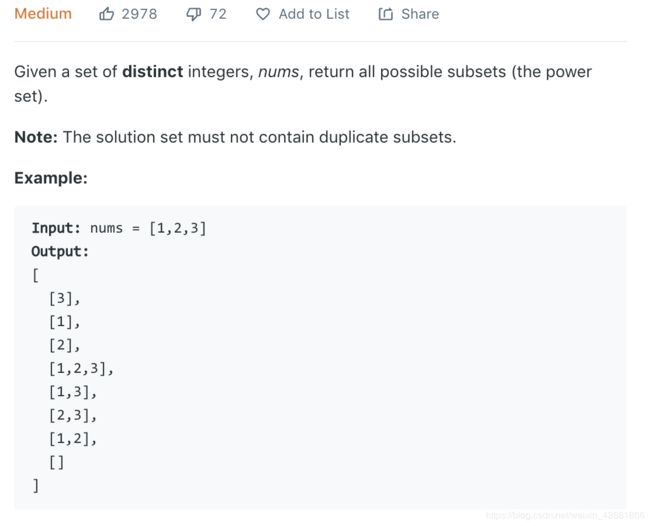
题意是直接给定一个数组,然后找出所有它的子集合,包括空数组[],看了combination sum套路,会发现这题简直太简单,直接依次遍历,将所有集合都加入结果集,不需要回溯,因为每个集合都属于需要的答案!代码如下:
class Solution4:
def subset(self,nums):
self.res = []
self.dfs(0,nums,[])
return self.res
def dfs(self,index,nums,path):
self.res.append(path) #每遍历一次就加入结果集,第一次调用加入[]空集
for i in range(index,len(nums)):
self.dfs(i+1,nums,path+[nums[i]])
90. Subsets II

这题和combination sum2的升级是一样的,提供了重复值,同时结果集不能包含同样的结果,所以它的处理方法和combination sum2的处理方法是一模一样的,先排序,然后针对遍历时前后数一样的直接跳过来加快处理速度,代码如下:
class Solution5(object):
def subsetsWithDup(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
self.res = []
nums.sort() #排序
self.dfs(0,nums,[])
return self.res
def dfs(self,index,nums,path):
self.res.append(path) #保持不变,满足条件的直接加入结果集
for i in range(index,len(nums)):
if i > index and nums[i] == nums[i-1]: #在这里控制,只要遍历时发现一样则跳过
continue
self.dfs(i+1,nums,path+[nums[i]])
79. Word Search

word search这道题就是迷宫类型,给定二维数组和1个单词,找出相邻的字母可以组成单词的存在,如果存在则返回true,否则false。这就有点像给你个二维数组组成的迷宫,只能上、下、左、右移动,当你到达出口(找到单词),则判定能走出去,否则不能走出去。
所以这题是按照迷宫类型的做法,不过区别是“入口”不知道在哪,也就是这个二维数组里的每一个都可能成为入口,所以需要双重for遍历将每一个数都作为入口的可能来尝试。当确定入口,接下来就是回溯的好戏,将它上下左右都作为一个下一步继续往下走,直到找到对应的数即可!所以递归终止条件是:1.找到单词;2.遍历时超过了边界;3.遍历时找到的数并不是需要的数
代码如下:
class Solution6:
def searchword(self,board,word):
self.res=[]
for i in range(len(board)):
for j in range(len(board[0])): #双重for遍历确定入口
if self.dfs(word,board,i,j): #如果返回true,则表明找到了单词
return True
return self.res
def dfs(self,word,board,i,j):
if not word:return True #基线条件1
if i <0 or j < 0 or i>len(board)-1 or j > len(board[0])-1 or board[i][j] != word[0]: #word每次找寻都是word[1:],基线条件2、3
return
tmp = board[i][j]
board[i][j] = "#" #这里要已经找过的标记为#,这样搜索时不会重复搜索
#下面的or即上下左右4种情况
res = self.dfs(word[1:],board,i+1,j) or self.dfs(word[1:],board,i-1,j) \
or self.dfs(word[1:],board,i,j+1) or self.dfs(word[1:],board,i,j-1)
board[i][j] = tmp #当”递“结束要”归“的时候,将标记为#的标记回来,便于第二次调用
return res
Unique Paths系列
62. Unique Paths

unique paths就是经典迷宫题型,而且其限制了只能向下、向右走,所以要考虑的方案反而少了。如上述题型,给定二维数组的格子数,从左上角走到右下角,一共有多少种走法?
这道题相对word search要简单不少,首先入口是确定的(0,0),而路线只有两种:向下、向右,基线条件:1.到达右下角;2.超出边界。结合这个就能确定代码:
class Solution7:
def unique_path(self, m, n):
count = self.dfs(0, 0, m - 1, n - 1) #二维数组坐标要小于真实长度1个单位
return count
def dfs(self, i, j, m, n):
if m < i or n < j: return 0 #超出边界
if i == m and j == n: #到达右下角,则算一种解法,所以count+1
return 1
count = self.dfs(i + 1, j, m, n) + self.dfs(i, j + 1, m, n)
return count
可以发现解法非常简单,但这里我们可以通过增加备忘录来加快速度。我们知道递归有一个非常浪费时间的资源是重复的节点会反复计算。比如下图从(0,0)到达(1,1)有两种方法,而(1,1)后面走的方式会通过递归完成。也就是说在下图,如果第1种已经走过(1,1)并记录下来(1,1)后续的走法,此时当地第2种到达(1,1)的时候,我们就可以直接通过”备忘录“返回结果来规避掉要继续(1,1)后续的递归!

讲起来很麻烦,实际上这个”备忘录“就是个哈希表,也就是字典,所以代码可以修改为如下:
class Solution7:
def unique_path(self, m, n):
self.memo = {} #增加记录的字典
count = self.dfs(0, 0, m - 1, n - 1)
return count
def dfs(self, i, j, m, n):
if (i, j) in self.memo: return self.memo[i, j] #如果存在,则直接返回备忘录的结果
if m < i or n < j: return 0
if i == m and j == n:
return 1
count = self.dfs(i + 1, j, m, n) + self.dfs(i, j + 1, m, n)
self.memo[i, j] = count
return count
63. Unique Paths II

unique path2相对于1增加了障碍物这个难度(因为题目过长,所以就没截那么多),并且转换了题型,原来是给定m、n的长度,现在是直接给个二维数组,但是解题思路是一样的,就是增加了个基线条件的判断:当碰到障碍物就回溯!
所以代码如下:
class Solution8(object):
def uniquePathsWithObstacles(self, obstacleGrid):
"""
:type obstacleGrid: List[List[int]]
:rtype: int
"""
self.memo = {}
m = len(obstacleGrid)
n = len(obstacleGrid[0]) #自定义m、n
count = self.dfs(0,0,m-1,n-1,obstacleGrid)
return count
def dfs(self,i,j,m,n,obstacleGrid):
if (i,j) in self.memo:return self.memo[i,j] #备忘录
if i > m or j > n:return 0
if obstacleGrid[i][j] == 1: return 0 #增加的基线条件,这里要注意的是要放到超出边界这个基线条件下面,不然就报错索引范围超过
if i==m and j ==n:return 1
count = self.dfs(i+1,j,m,n,obstacleGrid) + self.dfs(i,j+1,m,n,obstacleGrid)
self.memo[i,j] = count
return count
64. Minimum Path Sum

minimum path sum我也把它归结于unique path,实际上他近似于将”无权图“转变为”带权图“,即原先每个path的一个边等同于1,这里则是有具体的数字;原先只是求有多少种解法,这里则是要求出最小的解法!
此题要用到备忘录的话,也就是每个节点都需要找到最小的路径,此时可以通过min(r,d)来获取,r表示向右(right)走一步,d表示向下(down),取这两个值的最小值,即是这个节点的最小值。代码如下:
class Solution9(object):
def minPathSum(self, grid):
"""
:type grid: List[List[int]]
:rtype: int
"""
# if len(grid[0]) == 1:return grid[0][0]
self.memo = {}
m = len(grid)
n = len(grid[0])
res = self.dfs(0, 0, m - 1, n - 1, grid)
return res
def dfs(self, i, j, m, n, grid):
if (i, j) in self.memo: return self.memo[i, j]
if i == m and j == n: return grid[i][j] #到达右下角,返回对应的值
d = r = float('inf')
if i < m:
d = self.dfs(i + 1, j, m, n, grid)
if j < n:
r = self.dfs(i, j + 1, m, n, grid)
res = min(d, r) + grid[i][j] #每个结果都是当前值+向下和向右的最小值
self.memo[i, j] = res
return res
120. Triangle

这题简直就是上题的翻版,是求从顶到底的最小路径,而且每条路都只能选择相邻的值。相比上题有个好处是不用考虑右边的边界,只要考虑下边的边界,因为下边的值一定多于上边的值。所以代码基本可以照抄上面的:
class Solution10(object):
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
self.memo = {}
m = len(triangle)
res = self.dfs(0, 0, m - 1, triangle)
return res
def dfs(self, i, j, m, triangle):
if (i, j) in self.memo: return self.memo[i, j]
if i == m: return triangle[i][j]
l = self.dfs(i + 1, j, m, triangle)
r = self.dfs(i + 1, j + 1, m, triangle)
res = min(l, r) + triangle[i][j]
self.memo[i, j] = res
return res
总结
总共分享了11道题型的解法,可以发现都是一个套路,解题思路都大同小异,也就是制定遍历的规则和基线条件后,写出代码反而是最简单的了。而后面的那些可以用备忘录的,实际上基本都可以用动态规划来做,而动态规划的复杂度则要优先于回溯。这个下文再说~