最近发现DP的本质就是递归 + 缓存
占坑 后续补
经典的例子 爬楼梯 最小编辑距离 ...
- naive 递归
- 递归 + memo
- 直接DP
leetcode 72. Edit Distance 最小编辑距离
第一版解 很容易想到的递归解
class Solution(object):
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
if not word1 and not word2: # 0 0
return 0
if not word1 or not word2: # 01 10
return len(word1) or len(word2)
if word1[0] == word2[0]: # 相等的情况下直接考虑后面
return self.minDistance(word1[1:], word2[1:])
# 不相等的情况下考虑对当前元素 删除 插入 替换 操作数+1
return 1 + min(self.minDistance(word1[1:], word2), self.minDistance(word1, word2[1:]),
self.minDistance(word1[1:], word2[1:])) # 删除 插入 替换
超时
存在重复计算
例子 箭头表示重复计算的例子
md("horse", "hello")
md("orse", "ello")
md("orse", "llo")
md("orse", "lo")
md("rse", "llo") <-
md("rse", "lo")
md("rse", "ello")
md("rse", "llo") <-
md("se", "ello")
md("se", "llo") <<-
md("rse", "llo")
md("rse", "llo") <-
md("se", "llo") <<-
md("se", "lo")
递归 + memo
偷懒的写法 已经可以通过 但是比较慢 空间消耗也大
class Solution_memo(object):
def __init__(self):
self.memo = {} # 使用hash表存下已经计算过的解
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
if not word1 and not word2: # 0 0
return 0
if not word1 or not word2: # 01 10
return len(word1) or len(word2)
if word1[0] == word2[0]: # 相等的情况下直接考虑后面
return self.minDistance(word1[1:], word2[1:])
# 不相等的情况下考虑对当前元素 删除 插入 替换 操作数+1
if (word1, word2) not in self.memo:
self.memo[(word1, word2)] = 1 + min(self.minDistance(word1[1:], word2), self.minDistance(word1, word2[1:]),
self.minDistance(word1[1:], word2[1:])) # 删除 插入 替换
return self.memo[(word1, word2)]
优化 递归 + memo
此时时间空间都最优了
class Solution_memo_index(object):
def minDistance(self, word1, word2):
memo = {}
def dp(i, j):
if (i, j) not in memo: # 当前解没有计算过 计算出来 存入hash表
if i == len(word1) and j == len(word2):
res = 0
elif i == len(word1) or j == len(word2): # 确保只有一个东西非空
res = len(word1) - i or len(word2) - j # 确保只有一个东西非空
else:
if word1[i] == word2[j]:
res = dp(i + 1, j + 1)
else:
res = 1 + min(dp(i + 1, j), dp(i, j + 1), dp(i + 1, j + 1))
memo[(i, j)] = res
return memo[(i, j)]
return dp(0, 0)
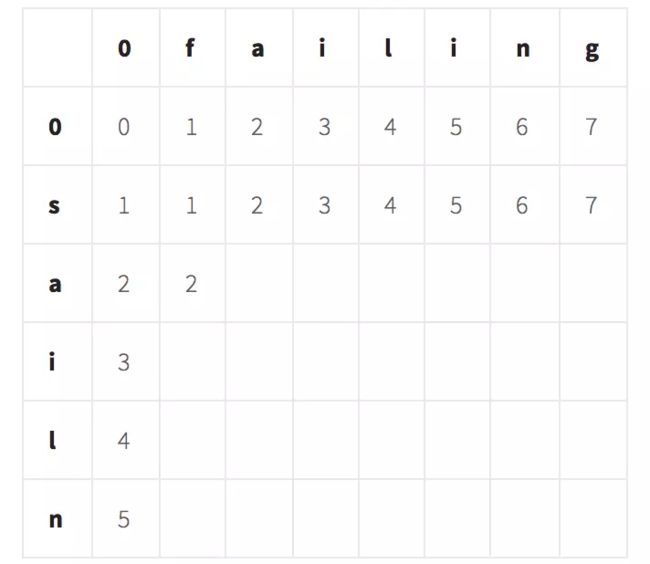
考虑存DP解呢
class Solution_(object):
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
n, m = len(word1), len(word2)
dp = [[0] * (m + 1) for _ in range((n + 1))] # 加1是为了让0可一计算
dp[0] = list(range(m + 1))
for i in range(n + 1):
dp[i][0] = i
for i in range(1, n + 1):
for j in range(1, m + 1):
if word1[i - 1] == word2[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
else:
dp[i][j] = 1 + min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) # 一定要实现a[:i] b[:j]实现匹配 使用之前的解
return dp[-1][-1]
学会画DP的表格
递归的方法比较好想
但是回过头来 发现直接写DP并不复杂啊...