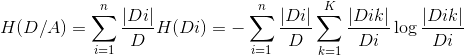本文思想及知识来源于对李航老师的统计学习方法的拜读，加上一些自己的理解整理，感谢李航老师伟大的著作：《统计学习方法》！
决策树是什么？(decision tree) 是一种分类与回归方法，主要用于分类，决策树模型呈现树形结构，是基于输入特征对实例进行分类的模型。我认为决策树其实是定义在特征空间与类空间上的条件概率分布！
使用决策树算法的主要步骤又是什么呢？ 可以分为三部分： 1特征的选取 2 决策树的生成 3 决策树的修剪
当前决策树的主要流行的三个算法是 ID3算法 C4.5算法和 CART算法(classification and regression tree)分类与回归树
本篇博客写作顺序是首先简单的介绍一下决策树的模型，然后按照决策树的算法的三个步骤对其进行详细的介绍
1 决策树模型
分类决策树模型是一种对实例进行分类的树形结构，其由结点（node）和有向边组成，而结点也分成内部结点和叶结点两种，内部结点表示的是一个特征和一个属性，叶结点表示具体的一个分类，这个地方一定要搞清楚.
用决策树进行分类，从根结点开始，对实例的某一个特征进行测试，根据测试结果分配往对应的子结点中去，每个子结点对应一个特征的取值，递归的进行分类测试和分配，最终到达对应的叶结点，完成本次的分类，这个过程就好像是大学生新生入学军训中分队伍，看你身高体重这一特征将你分配到正步排还是刺杀操排还是酱油排，一旦你进入了其中的某一个排就会再根据你正步走的好不好决定你具体在第几个班这样子，直到找到你合适的位置，对决策树来说就是找到了你合适的'类' classificaiton! 怀念一下我逝去的大学生活！向曾经的美好致敬～
接下来看一下具体的决策树到底是长什么样子(图片来自于网络)
2决策树的性质
这里对应着if-then规则，性质就是决策树是互斥且完备的，具体来说就是 每一个实例都被一条路径或者一条规则所覆盖，而且只能被一条路径和一条规则所覆盖，这个性质有点接近有且唯一这个意思，你想啊，总不能军训既让你去刺杀操又安排你去走正步吧，累死.....
3.决策树与条件概率分布
很多同学不理解，决策树，分类就分类，干嘛要和条件概率分布扯上关系啊，我本来概率论就学不好，非要说这些，其实从宏观上来讲，机器学习本来就是生成模型和判别模型两种，生成模型是根据训练数据学习模型生成的本质规律，而判别模型就是大家熟知的判别函数了，学习一个f=F(x),那么条件概率和决策树到底是怎么扯上关系的呢？
决策树表示给定特征条件下类的条件概率分布，这一条件概率分布定义了特征空间的一个划分，将特征空间划分成了互不相交的单元，并在每一个单元定义一个类的概率分布就构成了一个条件概率分布。决策树的一条路径对应于一个单元，决策树所表示的条件概率分布由各个单元给定条件下类的条件概率分布组成
4.决策树的学习
本小节探讨一下决策树学习的本质到底是什么，决策树就是从已知的训练数据中学习出一组分类规则，与训练数据不矛盾的决策树（也就是能对训练数据正确分类的决策树）,但是这种决策树可能有多个，也可能一个没有，我们需要的是一个既与训练数据矛盾较小同时模型的泛化能力又很强的决策树，也就是说我们要得到的决策树，不仅对训练数据的分类能力很强，其对未知数据的预测能力也要很强。
决策函数的学习过程必然少不了loss funciton 损失函数，如果不知道损失函数是什么的，建议回头补习一下基础知识，但是决策函数的损失函数怎么定义呢，其实loss function是一个正则化的极大似然函数(后面有解释)，我们学习的策略就是使得损失函数最小化，在损失函数意义下选择最有的决策树是一个NP完全问题，所以不得不采用启发式求解办法，寻找次优解，通过递归的方法来进行求解。具体操作如下：
1 通过某种评价准则选择一个最优的特征，利用该特征对训练数据进行分类切割，使得切割后的子集有一个相对最好的分类，这个过程对应着特征空间的划分也对迎着决策树分类的开始
2 如果此时子集基本已经正确分类则构建叶结点，将子集划分到叶结点中去，否则，对新的子集继续选择最优的特征继续分类，直至所有 的训练数据子集被正确分类完成为止，这样就生成了一颗决策树！
存在什么问题？
写到这里我想问一下这样构建的决策树有什么问题呢？聪明的你可能已经想到了，对，如此繁琐的分类过程形成的决策树难道不会存在过拟合问题吗？答案是肯定的，确实会存在过拟合的问题，也就是通过这个分类过程形成的决策树模型实在过于复杂，通俗点讲就是兄弟你想多了！我们拿到的数据其实根本没有想表达这个意思，有些玻璃心的人就会意淫出很多的意思来，是不是很累啊！那怎么解决这个问题呢，有个很形象的叫法----剪枝 没错，细枝末节全部剪掉，百万混音？autotune？这皇帝的新衣，我把它剥光！哈哈哈 ，跳戏了。。。。
说到底那剪枝到底是什么呢？
官话就是：对已生成的树自下而上进行剪枝，将树变得简单，从而使他具有很好的泛化能力，具体点就是去掉过于细分的叶结点，使其回退到父结点，甚至更高的结点，然后将父结点或者更高的结点改为新的叶结点！ 具体如何剪枝我们在介绍完了决策树算法再来详细介绍，进入本篇博客的重头戏！
一 特征选择
之前我们提到过，根据某种评价准则选取最优的特征，那么这种评价准则到底是什么？答：信息增益或者信息增益比
为什么进行特征的选择，因为有的特征分类的结果与随机分类根本没啥差别，就是混子，那么我们就成这种特征是不具备分类能力的，经验上扔掉这样的特征对分类的结果影响不大，所以需要利用信息增益或者信息增益比进行分类！
那么什么是信息增益呢？
说白了就是互信息！如果你不懂什么是互信息也没关系，我会介绍，在信息论中，熵是定义一个随机变量不确定性的度量，如果X是一个随机变量，它的概率分布为：P(X=xi)=Pi， i = 1,2,......n，则随机变量X的熵就定义为：
，并且我们认为的规定 0log0=0，当log分别以2和e为底数的时候计量单位就是比特和纳特
仔细观察公式我们发现，其实熵只和分布有关系，和分布的具体取值无关，希望读者仔细记住！所以H(x)=H(p)只和p有关
熵越大，随机变量的不确定性越大。
接下来我们通过联合概率分布引入条件熵的定义：
设有随机变量（X ,Y） 其联合概率分布为：
条件熵H(Y|X)就是指在已知随机变量X的条件下，随机变量Y的不确定性，随机变量X给定的条件下，随机变量Y的条件熵定义为X给定条件下Y的条件概率分布的熵对X的数学期望：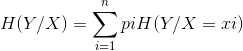
此处，pi指的是x的分布！
信息增益：特征A对训练数据集的D的信息增益g(D,A)，定义为集合D的经验熵与特征A给定条件下D的经验条件熵H(D/A)之差，即
其实这和互信息的定义是一样的，通俗的说就是，当得知特征A这个条件之后对对分类不确定性的消除量，再通俗一点就是当你得知特征A之后，对你分类的帮助是多少，直观的我们会选择首先采用帮助性最大的那个特征来进行分类，这也就是信息增益作为评价准则的直观思想。
这里补充一下经验熵和条件经验熵的概念，因为我们很多概率是不能够用训练数据直接得到的，只能说用已有的部分数据去估测它的结果，比如说极大似然估计，运用了估计概率所求得的熵和条件熵就称之为经验熵和经验条件熵，毕竟是通过经验得来的！
总结一下信息增益的算法步骤：（来自与李航老师课本）
输入：训练数据集和特征A
输出：特征A 对训练数据集D的信息增益g(D,A)
1 计算数据集D的经验熵H(D)：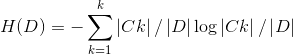
这里K 指的是训练数据的类别数，|Ck|指的是类k对应的样本数，而|D|则指的是训练样本的总个数
2计算特征A对数据集D的经验条件熵H(D|A): 
这个公式其实也不难理解，Di此处指的是特征A将训练样本D分成D1,D2,D3......Dn个单元，Dik则指的是Di个单元里面每一个类的数量，因为勤勉介绍了训练样本一共有k类，所以这样就可以解释的通这个公式了，黑话讲就是对特征A分成的每个小单元求经验熵，再利用经验概率对熵求平均，得到的就是条件经验熵！
3 计算信息增益
信息增益比
其实信息增益用来衡量特征的好坏其实是有弊端的，因为它总是偏向于选择取值较多的特征的问题，而使用信息增益比就可以很好的解决这个问题，接下来给出信息增益比的定义：
特征A 对训练数据集D的信息增益比Gr(D,A)定义为其信息增益与训练数据集关于特征A的值的熵Ha(D)之比:
再解释一下：
这样就得到了信息增益比的完整定义了！
决策树的生成算法
决策树的生成算法 主流的有两种 ID3和C4.5，主要的区别就是ID3用信息增益衡量特征选取，而C4.5用信息增益比衡量特征的选取，这里只介绍ID3 至于C4.5大同小异。
ID3算法：
输入 ：训练数据集，特征集A，阈值
输出：决策树
1若D中所有实例属于同一类Ck,则T为单结点树，并将类Ck作为该结点的标记，返回T
2 若A=
,则T为单结点树，并将D中实例数最大的类Ck作为该类的标记，返回T
3 否则，按照上述介绍信息增益的算法计算A中各特征对D的信息增益，选择信息增益最大的特征Ag
4如果Ag的信息增益小于阈值，则T为单结点树，并将D中实例数最大的类Ck作为该结点的标记，返回T
5 否则，对Ag的每一个可能值ai，Ag=ai，将D进行分割成非空子集Di,将Di中实例数最大的类作为标记，构建子结点，由结点及其子结点构成树T,返回T
6 对第i个子结点，以Di为训练集，以A-{Ag}为特征集递归的调用上述步骤，得到子树Ti,返回Ti
C4.5算法：
输入 ：训练数据集，特征集A，阈值
输出：决策树
1若D中所有实例属于同一类Ck,则T为单结点树，并将类Ck作为该结点的标记，返回T
2 若A=,则T为单结点树，并将D中实例数最大的类Ck作为该类的标记，返回T
3 否则，按照上述介绍信息增益比的算法计算A中各特征对D的信息增益，选择信息增益比最大的特征Ag
4如果Ag的信息增益小于阈值，则T为单结点树，并将D中实例数最大的类Ck作为该结点的标记，返回T
5 否则，对Ag的每一个可能值ai，Ag=ai，将D进行分割成非空子集Di,将Di中实例数最大的类作为标记，构建子结点，由结点及其子结点构成树T,返回T
6 对第i个子结点，以Di为训练集，以A-{Ag}为特征集递归的调用上述步骤，得到子树Ti,返回Ti
最后填坑，说一下决策树的剪枝：
其实决策树的剪枝，我最开始看决策树的时候这一部分是没读懂的，主要是因为我对正则化的一些概念不够熟悉，对其中的一些思想不够了解，我尽量讲的通俗一点，如果您还是没看懂，只能怪我表述能力不够咯，进入正题。
之前讲过，决策树容易出现过拟合的现象，就是细枝末节太多了，kris吴都看不过去，真的，这个没混直接发！那么我该如何进行决策树的修剪呢？
这里其实用到了一个平衡的思想，很简单
决策树的剪枝往往通过极小化决策树整体的损失函数或者代价函数实现，假设树的叶结点个数为|T|，t是树的一个叶结点，其上有Nt个样本，其中k类的样本有Ntk个，k=1,2,3...K，Ht(T)为叶结点上的经验熵，
参数大于0,那么决策树损失函数可以定义为：
而这其中经验熵为： 
将经验熵代入，可以得到公式：
解释一下，这里面C(T)指的是模型对训练数据的预测误差，而|T|表示的就是模型的叶结点个数，代表了模型的复杂度，起到了控制平衡两者之间的作用的一个角色，=0意味着只考虑对训练数据的预测误差而不考虑结点个数，模型负责度，自然会有过拟合的现象产生。
所谓的剪枝，就是当确定的时候，选择损失函数最小的模型，确定时候，子树越大，训练数据拟合程度越好，但是泛化能力就越差，相反的，子树越小，模型的复杂度就越小，对训练数据的拟合程度越差，但是泛化能力相对较好，损失函数同时考虑二者的影响，达到一个平衡的最优！
本质上 这样的损失函数最小化原则就是等价与正则化的极大似然估计，利用损失函数最小化原则进行剪枝，就是利用正则化的极大似然估计进行模型的筛选！
希望各位读完了之后，能够对决策树有更进一步的理解，有什么问题可以随时在下面留言，大家一起讨论！