RuntimeWarning: overflow encountered in exp
今天在sigmoid 函数中使用 numpy.exp 的时候,遇到了 RuntimeWarning: overflow encountered in exp ,看到其他人的博客里面的解决方法。
# https://www.cnblogs.com/zhhy236400/p/9873322.html
def sigmoid(inx):
if inx>=0: #对sigmoid函数的优化,避免了出现极大的数据溢出
return 1.0/(1+exp(-inx))
else:
return exp(inx)/(1+exp(inx))
作者其实说清楚了,但是我自己看得时候,总觉得不太直观,差那么一点意思。于是就自己写一下。
f ( x ) = e x f(x) = e^x f(x)=ex 的函数如下图:
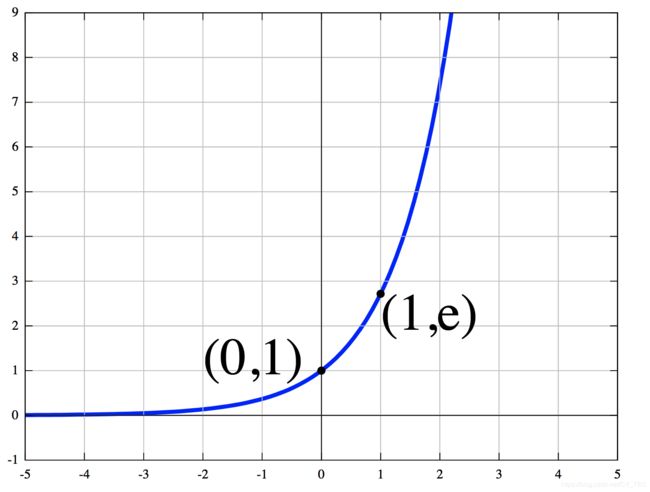
x > = 0 x >= 0 x>=0 时, e x e^x ex 随 x x x 增长比较快,就很容易上溢。
对于 sigmoid 函数,
s i g m o i d = 1 1 + e − x sigmoid = \frac{1}{1 + e^{-x}} sigmoid=1+e−x1
如果在使用过程中 x < 0 x < 0 x<0 , e − x e^{-x} e−x 就非常容易上溢。
RuntimeWarning: overflow encountered in exp 和 sigmoid 本身没有关系,只和 e − x e^{-x} e−x 有关。
- x < 0 , 令 t = − x , 则 t > 0 , e t x < 0, 令 t = -x, 则t > 0, e^t x<0,令t=−x,则t>0,et 就非常容易上溢出。
- x > 0 , 令 t = − x , 则 t < 0 , e t ∈ ( 0 , 1 ) x > 0, 令 t = -x, 则t < 0, e^t \in (0, 1) x>0,令t=−x,则t<0,et∈(0,1) 就不会有什么问题。
而
1 1 + e − x = e x e x + 1 \frac{1}{1 + e^{-x}} = \frac{e^x}{e^{x} + 1} 1+e−x1=ex+1ex
那么就可以根据 x x x 是否大于零,来选择两个公式。
但是 x < 0 x < 0 x<0 时, e x e^x ex 同样有下溢的风险。
只是 numpy 报了 warning ,而 python 没有报而已,两者并没有任何差别。
参考:
https://www.cnblogs.com/zhhy236400/p/9873322.html