神经网络—线性神经网络，Delta学习规则
一：线性神经网络
线性神经网络在结构上与感知器非常相似，只是激活函数不同。 在模型训练时把原来的sign函数改成了purelin函数：y = x
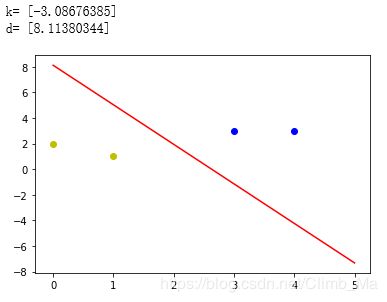
- 线性神经网络简单二分类程序举例（与单层感知器例子相同）
import numpy as np
import matplotlib.pyplot as plt
#输入数据
X = np.array([[1,3,3],
[1,4,3],
[1,1,1],
[1,0,2]])
#标签
Y = np.array([[1],
[1],
[-1],
[-1]])
#权值初始化，3行1列(指三输入一输出)，取值范围-1到1
W = (np.random.random([3,1])-0.5)*2
print(W)
#学习率设置
lr = 0.11
#神经网络输出
O = 0
def update():
global X,Y,W,lr
O = np.dot(X,W) #shap:(3,1)
W_C = lr*(X.T.dot(Y-O))/int(X.shape[0])
W = W + W_C
随机产生三个权值：
for i in range(100):
update()
#正样本
x1 = [3,4]
y1 = [3,3]
#负样本
x2 = [1,0]
y2 = [1,2]
#计算分界线的斜率以及截距
k = -W[1]/W[2]
d = -W[0]/W[2]
print('k=',k)
print('d=',d)
xdata = (0,5)
plt.figure()
plt.plot(xdata,xdata*k+d,'r')
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='y')
plt.show()
输出：
二：Delta学习规则
- 1986年，认知心理学家McClelland和Rumelhart在神 经网络训练中引入了δ规则，该规则也可以称为连续感知器学习规则。
- δ学习规则是一种利用梯度下降法的一般性的学习规则。
- 代价函数(损失函数)(Cost Function,Lost Function)
二次代价函数：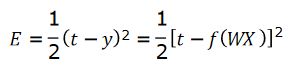
误差E是权向量W的函数，我们可以使用梯度下降法来最小化
E的值：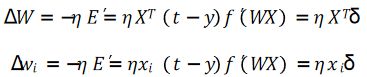
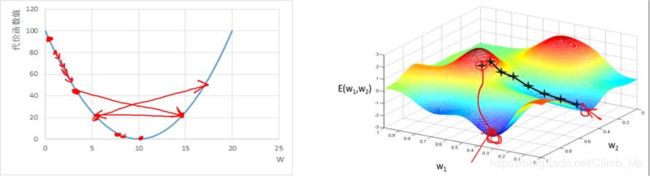
- 梯度下降法的问题
学习率难以选取，太大会产生震荡，太小收敛缓慢;
容易陷入局部最优解(局部极小值).
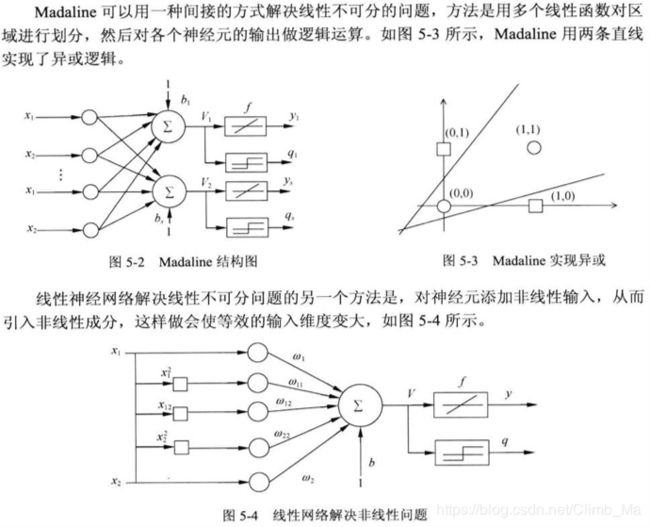
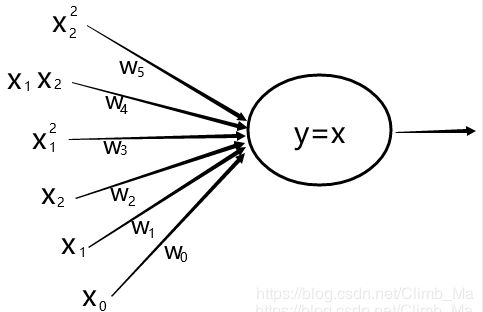
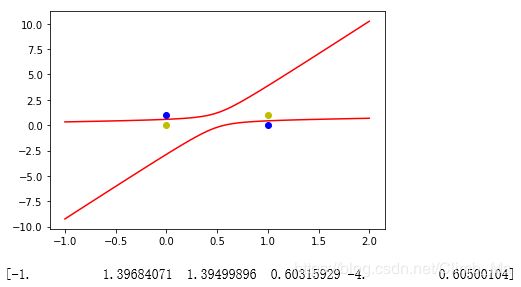
三：线性神经网络解决异或问题
- 线性神经网络解决异或问题程序举例
加入非线性输入
import numpy as np
import matplotlib.pyplot as plt
#输入数据
X = np.array([[1,0,0,0,0,0],
[1,0,1,0,0,1],
[1,1,0,1,0,0],
[1,1,1,1,1,1]])
#标签
Y = np.array([-1,1,1,-1])
#权值初始化，3行1列(指三输入一输出)，取值范围-1到1
W = (np.random.random([6])-0.5)*2
print(W)
#学习率设置
lr = 0.11
#计算迭代次数
n = 0
#神经网络输出
O = 0
def update():
global X,Y,W,lr,n
n+=1
O = np.dot(X,W.T) #shap:(3,1)
W_C = lr*((Y-O.T).dot(X))/int(X.shape[0])
W = W + W_C
随机产生6个权值
[-0.82960072 0.9781251 0.20617343 0.18444368 -0.7360009 -0.58382449]
for i in range(10000):
update()
x1 = [0,1]
y1 = [1,0]
#负样本
x2 = [0,1]
y2 = [0,1]
def calculate(x,root):
a = W[5]
b = W[2]+x*W[4]
c = W[0]+x*W[1]+x*x*W[3]
if root==1:
return (-b+np.sqrt(b*b-4*a*c))/(2*a)
if root==2:
return (-b-np.sqrt(b*b-4*a*c))/(2*a)
xdata = np.linspace(-1,2)
plt.figure()
plt.plot(xdata,calculate(xdata,1),'r')
plt.plot(xdata,calculate(xdata,2),'r')
plt.plot(x1,y1,'bo')
plt.plot(x2,y2,'yo')
plt.show()
print(W)
输出
O = np.dot(X,W.T)
print(O)
输出：[-1. 1. 1. -1.]