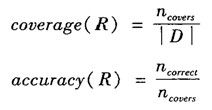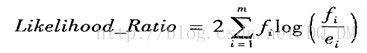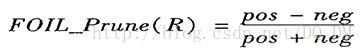第八章 基于规则的分类
1、使用IF-THEN规则分类
规则是表示信息或少量知识的好方法。基于规则的分类器使用一组IF—THEN规则进行分类。一个IF—THEN规则是一个如下的表达式:
IF条件THEN结论
规则R1是一个例子:
R1:IF age=youth AND student=yes THEN buys_computer=yes
也可以写作
R1:(age=youth)^(student=yes)=>(buys_computer=yes)
规则的“IF”部分(或左部)称为规则的前件或前提。规则前件由一个或多个用逻辑连接词AND连接的属性测试(例如,age=youth和student=yes)组成。
THEN部分(或右部)是规则的结论。规则的结论包含一个类预测(在这个例子中,预测顾客是否购买计算机)。
对于给定的元组,如果规则前件中的条件(即所有的属性测试)都成立,则我们说规则前件被满足,并且规则覆盖该元组。
规则R可以用它的覆盖率和准确率来评估。给定类标记的数据集D中的一个元组X,设ncovers为覆盖的元组数,ncorrect为R正确分类的元组数,可以将R的覆盖率和准确率定义为:
也就是说,规则的覆盖率是规则覆盖的元组的百分比。对于规则的准确率,考察在它覆盖的元组中,可以被规则正确分类的元组所占的百分比。
让我们来看看如何使用基于规则的分类来预测给定元组X的类标号。
如果规则被X满足,则称该规则被触发。例如,假设有:X=(age=youth,income=medium,student=yes,credit_rating=fair)想根据buys_computer对X分类。X满足R1,触发该规则。
如果R1是唯一满足的规则,则该规则被激活,返回X的分类预测。注意,触发并不总意味着激活,因为可能有多个规则被满足!
可能存在的问题:(1)如果多个规则被触发,但是它们指定了不同的类(2)没有一个规则被X满足。
解决办法:(1)如果多个规则被触发,则需要一种解决冲突的策略来决定激活哪一个规则,并对X指派它的类预测。由许多可能的策略。我们考察两种,即规模序和规则序。
规模序:把最高优先权赋予具有“最苛刻”要求的被触发的规则,其中苛刻性用规则前件的规模度量。也就是说,激活具有最多属性测试的被触发的规则。
规则序:预先确定规则的优先次序。这种序可以是基于类的或基于规则的。
基于类的序:类按“重要性”递减排序,如按普遍性的降序排序。作为选择,它们也可以根据每个类的误分类代价排序。每个类中的规则(可能有很多)是无序的,当然,它们也不必要有序,因为它们都预测相同的类,所以不会存在冲突问题。
基于规则的序:根据规则质量的度量,如准确率、覆盖率或规模(规则前件中属性测试数),或者根据领域专家的建议,把规则组织成一个优先权列表。在使用规则排序时,规则集称为决策表。使用规则序,最先出现在决策表中的被触发的规则具有最高优先权,因此激活它的类预测。满足X的其他规则都被忽略。大部分基于规则的分类系统都使用基于类的规则序策略。
(2)没有一个规则被X满足的条件下,我们可以建立一个省缺或默认规则(条件为空),根据训练集指定一个默认类。这个类可以是多数类,或者不被任何规则覆盖的元组的多数类。当且仅当没有其他规则覆盖X时,最后才使用默认规则(该规则被激活)。
下面我们考察如何建立基于规则的分类器(也就是,如何获取IF-THEN规则)?
2、由决策树提取规则
与决策树相比,IF-THEN规则可能更容易理解,特别是当决策树非常大时更是如此。
为了从决策树提取规则,对每条从根到树叶节点的路径创建一个规则。
(1)前件:沿着给定路径上的每个分裂准则的逻辑AND形成规则的前件。
(2)后件:存放类预测的树叶结点形成规则的后件。
由于这些规则直接从树中提取,所以它们是互斥的和穷举的。
(1)互斥意味着不可能存在规则冲突,因为没有两个规则被相同的元组触发。(每个树叶有一个并且任何元组都只能映射到一个树叶。)
(2)穷举意味着对于每种可能的属性—值组合都存在一个规则,使得该规则集不需要默认规则。因此,规则的序不重要—它们是无序的。
由于每个树叶一个规则,所以提取的规则集并不比对应的决策树简单多少!在某些情况下,提取的规则可能比原来的树更难解释(比如,子树中存在重复和复制)。提取的规则集可能很大并且难以理解,因为某些属性测试可能是不相关的和冗余的。尽管很容易从决策树提取规则,但是可能需要做更多的工作,对结果规则集进行剪枝。
“如何修剪规则集?”对于给定的规则前件,不能提高规则的估计准确率的任何条件都可以剪掉(即删除),从而泛化该规则。
3、使用顺序覆盖算法的规则归纳
顺序覆盖算法可以直接从训练数据集提取IF-THEN规则(即不必产生决策树),是最广泛使用的挖掘分类规则析取集的方法。算法的名字源于规则被顺序地学习(一次一个),其中给定类的每个规则覆盖该类的许多元组(并且希望不覆盖其他类的元组)。
有许多流行的顺序覆盖算法,包括AQ,CN2和最近提出的PIPPER。
算法的一般策略如下:一次学习一个规则,每学习一个规则,就删除该规则覆盖的元组,并在剩下的元组上重复该过程。
基本顺序覆盖算法显示在下图中。这里,一次为一个类学习规则。理想情况下,在为C类学习规则时,我们希望覆盖C类的所有(或许多)训练元组,并且没有(或很少)覆盖其他类的元组。这样,学习的规则应该具有高准确率。规则不必是高覆盖率的。这是因为每个类可以有多个规则,使得不同的规则可以覆盖同一个类中的不同元组。该过程继续,直到满足某终止条件,如不再有训练元组,或返回规则的质量低于用户指定的阈值。
“如何学习规则?”典型地,规则以从一般到特殊的方式增长(见下图)。我们可以将这想象成束状搜索,从空规则开始,然后逐渐向它添加属性测试。添加的属性测试作为规则前件条件的逻辑合取。
图中,为了学习“accept”类的规则,从最一般的规则开始,即从规则前件条件为空的规则开始。该规则是:IF THEN loan_decision=accept 然后,我们考虑每个可以添加到该规则中的可能属性测试。这些可以从参数Att-vals导出,该参数包含属性及其相关联值的列表。例如,对于属性-值对(att,val),可以考虑诸如att=val,att<=val,att>val等测试。
通常,训练数据包含许多属性,每个属性都有一些可能的值。找出最优规则集是昂贵的。或者,Learn_One_Rule采用一种贪心的深度优先策略。每当面临添加一个新的属性测试(合取项)到当前规则时,它根据训练样本选择最能提高规则质量属性的测试。
1.规则质量的度量
Learn_One_Rule需要度量规则的质量。每当考虑一个属性测试时,它必须检查,看添加该测试到规则的条件中是否导致一个改进的规则。
举例验证准确率本身并非规则质量的可靠估计。
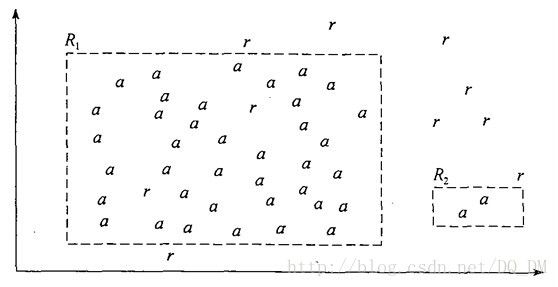
考虑下图中所示的两个规则。这两个规则都是loan_decision=accept类的规则。使用“a”表示“accept”类的元组,“r”表示“reject”类的元组。规则R1正确地对它所覆盖的40个元组中的38个进行了分类,规则R2只覆盖了2个元组,它正确地进行了分类。它们的准确率分别为95%和100%。这样,R2比R1具有更高的准确率。然而,由于小覆盖率,R2不是更好的规则。
图 Loan_decision=accept类的规则,显示accept(a)和accept(r)元组
这个例子告诉我们准确率本身不是规则质量的可靠估计。当然,覆盖率本身也没有用——对于给定的类,可以构造一个规则,它覆盖许多元组,大部分属于其他类。因此,寻找其他度量,可以集成准确率和覆盖率。
现在,我们将考察几种度量:(1)熵(2)基于信息增益的度量(3)考虑覆盖率的统计检验。
为了便于讨论,假设学习类C的规则。当前的规则是R:IFcondition THEN class=C 给定属性测试逻辑合取后的条件为condition’,也就是,R’: IFcondition’ THEN class=C,我们想知道R’是否比R更好。
熵又称为对数据集D的元组分类所需要的期望信息。这里,D是condition’覆盖的元组集合,而pi是D中Ci类的概率。熵越小,condition’越好。熵更偏向于覆盖单个类大量元组和少量其他类元组的条件。
另一种度量基于信息增益,在一阶归纳学习器(First Order Inductive Learner,FOIL)中提出。
FOIL是一种学习一阶逻辑规则的顺序覆盖算法。学习一阶逻辑规则更为复杂,因为这种规则包含变量,而平时我们关心的规则都是命题(即不含变量)。
在机器学习中,用于学习规则的类的元组称正元组,而其余元组为负元组。设pos(neg)为被R覆盖的正(负)元组数。设pos’(neg’)为被R’覆盖的正(负)元组数。FOIL用下式估计扩展condition’而获得的信息
它偏向于具有高准确率并且覆盖许多正元组的规则。
还可以用统计显著性检验来确定规则的效果是否并非出于偶然性,而是预示属性值与类之间的真实相关性。该检验将规则覆盖的元组的观测类分布与规则随机检测产生的期望类分布进行比较。我们希望评估这两个分布之间的观测是否是随机的。可以使用似然率估计量
其中m是类数。
对于满足规则的元组,fi是这些元组中类i的观测频率,ei是规则随机预测时类i的期望频率。该统计量服从自由度为m-1的卡方分布。似然率越高,规则正确预测数与“随机猜测器”的差越显著。也就是说,规则的性能并非偶然性。似然率有助于识别具有显著覆盖率的规则。
2.规则剪枝
上面介绍的规则质量评估使用原训练数据的元组,可能过分拟合。为了补偿这一点,可以对规则剪枝。通过删除一个合取(属性测试)对规则剪枝。选择对规则R剪枝,如果在独立的元组集上评估,R剪枝后的版本具有更高的质量。与决策树剪枝一样,称这个元组集为剪枝集。可以使用各种剪枝策略,如前面介绍的悲观剪枝方法。
FOIL使用一种简单但有效的方法。给定规则R,
其中,pos和neg分别为规则R覆盖的正元组数和负元组数。这个值将随着R在剪枝集上的准确率的增加而增加。因此,如果R剪枝后版本的POIL_Prune值较高,则对R剪枝。