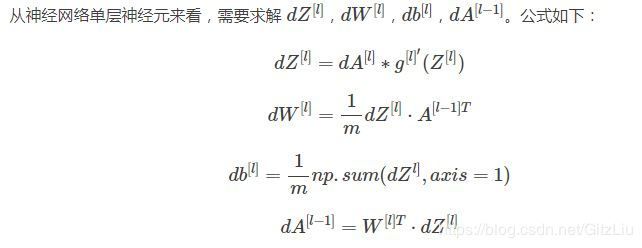DNN实战-猫狗分类
以下是正文
深层的神经网络来解决一个猫、狗的分类问题。这是一个典型的二分类问题。输入是一张图片,我们会把 3 通道的 RGB 图片拉伸为一维数据作为神经网络的输入层。神经网络的输出层包含一个神经元,经过 Softmax 输出概率值
P,若 P>0.5,则判断为猫(正类),若 P≤0.5,则判断为非猫(负类)。
对于整个神经网络模型,我们可以选择使用不同层数,以此来比较模型分类的性能,从而得到较深的神经网络及分类效果更好的结论。但这也不是绝对的,并不是说网络层数越多越好。接下来,我就带大家一步步构建神经网络模型。
阅读建议:结合目录中第“【11】解析”部分来看整个项目
【0】导入数据集
import skimage.io as io
import numpy as np
# 训练样本
file='./data/train/*.jpg'
coll = io.ImageCollection(file)
# 500 个训练样本,250 个猫图片,250 个非猫图片
X_train = np.asarray(coll)
# 输出标签
y_train = np.hstack((np.ones(250),np.zeros(250)))
# 测试样本
file='./data/test/*.jpg'
coll = io.ImageCollection(file)
# 200 个训练样本,100 个猫图片,100 个非猫图片
X_test = np.asarray(coll)
# 输出标签
y_test = np.hstack((np.ones(100),np.zeros(100)))
m_train = X_train.shape[0]
m_test = X_test.shape[0]
w, h, d = X_train.shape[1], X_train.shape[2], X_train.shape[3]
print('训练样本数量:%d' % m_train)
print('测试样本数量:%d' % m_test)
print('每张图片的维度:(%d, %d, %d)' % (w, h, d))
运行以上程序,输出结果为:
训练样本数量:500
测试样本数量:200
每张图片的维度:(64, 64, 3)
【1】预处理
# 图片矩阵转化为一维向量
X_train = X_train.reshape(m_train, -1).T
X_test = X_test.reshape(m_test, -1).T
print('训练样本维度:' + str(X_train.shape))
print('测试样本维度:' + str(X_test.shape))
# 图片像素归一化到 [0,1] 之间
X_train = X_train / 255
X_test = X_test / 255
上述代码中,reshape 作用就是将图片尺寸调整为一维数组。
输出结果为:
训练样本维度:(12288, 500)
测试样本维度:(12288, 200)
【2】初始化参数 W 和 b
首先,我们定义 layer_dims,用来存储神经网络各层数的列表,使用 parameters 字典存储各层参数 W 和 b,定义过程如下:
def initialize_parameters(layer_dims):
parameters = {} # 存储参数 W 和 b 的字典
L = len(layer_dims) # 神经网络的层数,包含输入层
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1]) * 0.1
parameters['b' + str(l)] = np.zeros((layer_dims[l],1))
return parameters
以上代码将 W 初始化为均值 0,方差为 0.1 的服从高斯分布随机值(注意,w不能像b一样初始化为0,这样无法求目标函数对权值w的导数)
将 b 全部初始化为 0。需要注意 W 和 b 的维度不要写错。
【3】正向传播单层神经元
神经网络正向传播过程中,单个神经元的运算包括两个步骤:线性运算和激活函数,而激活函数又根据所在的网络层,选择 Sigmoid 或者 ReLU。首先来定义单个神经元的运算函数:
# sigmoid 函数
def sigmoid(Z):
A = 1/(1+np.exp(-Z))
return A
# relu 函数
def relu(Z):
A = np.maximum(0,Z)
return A
# 单个神经元运算单元
def linear_activation_forward(A_prev, W, b, activation):
Z = np.dot(W, A_prev) + b # 线性输出
if activation == "sigmoid":
A = sigmoid(Z)
elif activation == "relu":
A = relu(Z)
cache = (A_prev, W, b, Z)
return A, cache
正向传播 L 层神经元,前 L-1 层使用的激活函数是 ReLU,最后一层使用的激活函数是 Sigmoid。可以使用 for 循环来构建整个正向传播过程:
def model_forward(X, parameters):
caches = []
A = X
L = len(parameters) // 2 # 神经网络层数 L
# L-1 层使用 ReLU
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], "relu")
caches.append(cache)
# L 层使用 Sigmoid
AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], "sigmoid")
caches.append(cache)
return AL, caches
【4】损失函数
def compute_cost(AL, Y):
m = AL.shape[1]
cost = -1/m*np.sum(Y*np.log(AL)+(1-Y)*np.log(1-AL))
cost = np.squeeze(cost) # 压缩维度,保证损失函数值维度正确,例如 [[10]] -> 10
return cost
【5】反向传播单层神经元
def relu_backward(dA, Z):
dZ = np.array(dA, copy=True)
dZ[Z <= 0] = 0
return dZ
然后需要定义 Sigmoid 的求导函数:
def sigmoid_backward(dA, Z):
s = 1/(1+np.exp(-Z))
dZ = dA * s * (1-s)
return dZ
接下来是定义单层神经元反向传播函数:
def linear_activation_backward(dA, cache, activation):
A_prev, W, b, Z = cache
if activation == "relu":
dZ = relu_backward(dA, Z)
elif activation == 'sigmoid':
dZ = sigmoid_backward(dA, Z)
m = dA.shape[1]
dW = 1/m*np.dot(dZ,A_prev.T)
db = 1/m*np.sum(dZ,axis=1,keepdims=True)
dA_prev = np.dot(W.T,dZ)
return dA_prev, dW, db
前 L-1 层使用的激活函数是 ReLU,最后一层使用的激活函数是 Sigmoid。可以使用 for 循环来构建整个反向传播过程:
def model_backward(AL, Y, caches):
grads = {}
L = len(caches) # 神经网络层数,包括输入层
m = AL.shape[1] # 样本个数
Y = Y.reshape(AL.shape) # 保证 Y 与 AL 维度一致
# AL 值
dAL = -(np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))
# 第 L 层,激活函数是 Sigmoid
current_cache = caches[L-1]
grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation = "sigmoid")
# 前 L-1 层,激活函数是 ReLU
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 1)], current_cache, activation = "relu")
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
return grads
【6】更新网络参数 W 和 b
def update_parameters(parameters, grads, learning_rate):
L = len(parameters) // 2 # 神经网络层数,包括输入层
for l in range(L):
parameters["W" + str(l+1)] -= learning_rate*grads["dW" + str(l+1)]
parameters["b" + str(l+1)] -= learning_rate*grads["db" + str(l+1)]
return parameters
【7】整个神经网络模型
讨论完正向传播、损失函数计算、反向传播、更新 W 和 b 之后,我们将所有的模块组合起来构成整个神经网络。整个模型定义如下:
def nn_model(X, Y, layers_dims, learning_rate = 0.01, num_iterations = 3000, print_cost=False):
np.random.seed(1)
costs = []
# 参数初始化
parameters = initialize_parameters(layers_dims)
# 迭代训练
for i in range(0, num_iterations):
# 正向传播
AL, caches = model_forward(X, parameters)
# 计算损失函数
cost = compute_cost(AL, Y)
# 反向传播
grads = model_backward(AL, Y, caches)
# 更新参数
parameters = update_parameters(parameters, grads, learning_rate)
# 每迭代 100 次,打印 cost
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
if print_cost and i % 100 == 0:
costs.append(cost)
# 绘制 cost 趋势图
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per hundred)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
【8】模型预测
模型搭建完毕之后,就可以使用训练好的模型对新样本进行预测。
def predict(X, y, parameters):
m = X.shape[1]
p = np.zeros((1,m))
# 正向传播
AL, caches = model_forward(X, parameters)
predictions = AL > 0.5
accuracy = np.mean(predictions == y)
print("Accuracy: %f" % accuracy)
return predictions
神经网络输出层进行预测,若输出 P>0.5,则判断为正类,若输出 P≤0.5,则判断为负类。predict 输出预测准确率。
【9】训练模型
下面开始训练神经网络模型,为了比较网络层数不同对准确率的影响,我们先设计一个简单的两层神经网络。
layers_dims = [12288, 10, 1] # 2-layer model
parameters = nn_model(X_train, y_train, layers_dims, learning_rate = 0.01, num_iterations = 1500, print_cost = True)
print 函数输出如下内容:
Cost after iteration 0: 0.934291
Cost after iteration 100: 0.654145
Cost after iteration 200: 0.598071
Cost after iteration 300: 0.491806
Cost after iteration 400: 0.952094
Cost after iteration 500: 0.426875
Cost after iteration 600: 0.838886
Cost after iteration 700: 0.832011
Cost after iteration 800: 0.218174
Cost after iteration 900: 0.190239
Cost after iteration 1000: 0.424622
Cost after iteration 1100: 0.181183
Cost after iteration 1200: 0.243990
Cost after iteration 1300: 0.125354
Cost after iteration 1400: 0.179002
该模型,输入层神经元只包含了单隐藏层,隐藏层个数为 10,学习因子为 0.01,迭代训练 1500 次,每隔 100 次打印损失函数值。损失函数随迭代次数的变化趋势如下图所示,整体降低,但振荡较大。
计算训练样本的准确率:
pred_train = predict(X_train, y_train, parameters)
执行结果如下:
Accuracy: 0.984000
测试样本的准确率:
pred_test = predict(X_test, y_test, parameters)
执行结果如下:
Accuracy: 0.570000
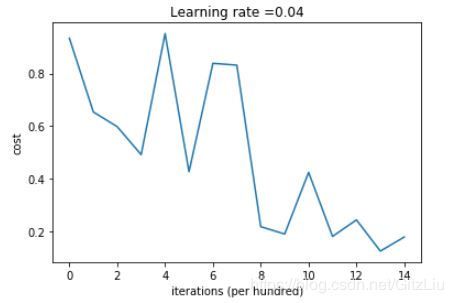
【10】较复杂神经网络
再设计一个较复杂的五层神经网络:
layers_dims = [12288, 100, 50, 10, 4, 1] # 5-layer model
parameters = nn_model(X_train, y_train, layers_dims, learning_rate = 0.04, num_iterations = 1500, print_cost = True)
print 函数输出如下内容:
Cost after iteration 0: 0.693274
Cost after iteration 100: 0.693000
Cost after iteration 200: 0.692647
Cost after iteration 300: 0.692013
Cost after iteration 400: 0.690574
Cost after iteration 500: 0.686974
Cost after iteration 600: 0.675996
Cost after iteration 700: 0.646076
Cost after iteration 800: 0.626832
Cost after iteration 900: 0.561664
Cost after iteration 1000: 0.521846
Cost after iteration 1100: 0.460633
Cost after iteration 1200: 0.337490
Cost after iteration 1300: 0.232980
Cost after iteration 1400: 0.051204
该模型,输入层神经元只包含了 4 层隐藏层,隐藏层个数分别为 100、50、10、4,学习因子为 0.04,迭代训练 1500 次,每隔 100 次打印损失函数值。损失函数随迭代次数的变化趋势如下图所示,整体降低,但振荡较小。

训练样本的准确率:
pred_train = predict(X_train, y_train, parameters)
执行结果如下:
Accuracy: 0.998000
测试样本的准确率:
pred_test = predict(X_test, y_test, parameters)
执行结果如下:
Accuracy: 0.625000
通过对比能够看到,随着神经网络层数的加深,训练样本准确率和测试样本准确率与随之增加了,其实主要看的是测试样本准确率。事实上,测试样本的准确率并没有提高多少,原因是对于复杂图片的分类,单纯靠增加神经网络层数并不能有效提高模型的性能,还需要其它更高效的优化算法,包括梯度的优化算法、学习率的优化策略、权重初始化方法等等。关于神经网络各种常用的优化方法我们后面做详细介绍。
完整代码过一阵会放在github上。
【11】解析
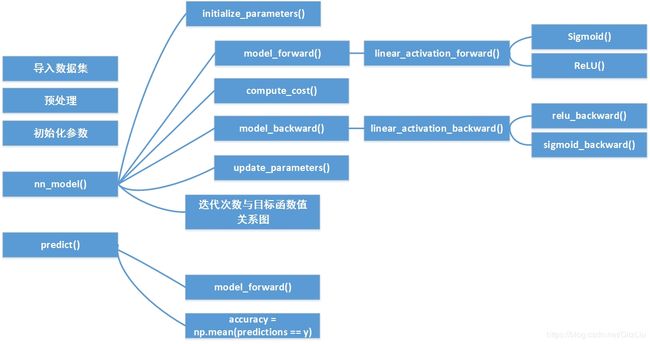
DNN 中函数调用关系
0、流程
(1)处理样本 为64*64*3的一个一维向量 (3是通道)将图 整理为一个样本 500个样本 即(64*64*3,500) 样本空间
(2)针对所有样本的 正向 反向传播过程 (一次,第(3)步是多次)
(3)然后针对所有样本 做一个大循环 所有样本的 多次(具体是迭代次数决定)正向 反向传播过程 nn_model
(4)预测(测试集与训练集同样处理)
1、图中“初始化参数” 解释
其实就是initialize_parameters()函数,在nn_model()中写了,因此,“初始化参数” 就没写。
2、部分函数解释
定义 ReLU 的求导函数: relu_backward()
定义 Sigmoid 的求导函数:sigmoid_backward()
3、nn_model()伪代码
nn_model 包含整个模型所有的东西 返回的是参数 parameters字典 key是w 和 b
看nn_model()的伪代码:
def nn_model():
initialize_parameters()
for i in range(0, num_iterations):
model_forward()
compute_cost()
model_backward()
update_parameters()
plt.show()
plt.show()画的是 迭代次数与目标函数值的关系图。
4、predict伪代码
predict 预测,这个里面输入是 (X, y, parameters) parameters是步骤3训练好的
看predict伪代码,可以看出预测过程只有正向了,没有反向过程了,因为反向过程是为了训练参数的,现在只有正向了
def predict(X, y, parameters):
AL, caches = model_forward(X, parameters)
# 输出结果AL 预测过程只有正向了,没有反向过程了,因为反向过程是为了训练参数的,现在只有正向了
predictions = AL > 0.5
accuracy = np.mean(predictions == y) #预测
5、nn_model()中参数
nn_model(X_train, y_train, layers_dims, learning_rate = 0.01, num_iterations = 1500, print_cost = True)
(1)X_train 数据集
(2)y_train 标签
(3)layers_dims
layers_dims = [12288, 10, 1] # 2-layer model
12288是输入层节点 即将图片展开成一维向量 64643
10是 隐藏的节点个数
1 是输出层的节点个数
(隐藏节点个数根据什么来定的呢?)
损失函数 与 迭代次数的图是在 nn_model中的
(4)learning_rate
这个是值是在参数更新的时候,
w = w - learning_rate * 梯度
(5)num_iterations 迭代次数
(6)print_cost 是否要定期输出迭代值
print_cost 是bool值,这个设置巧妙,类似的,那也可以设置是否要画图
6、注意各个函数中的for循环
(1)initialize_parameters(layer_dims)中的
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1]) * 0.1
parameters['b' + str(l)] = np.zeros((layer_dims[l],1))
L是层数
对每一层 的w和b 赋值,注意赋的是矩阵
(2)model_forward(X, parameters)中的
for l in range(1, L):
A_prev = A
A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], "relu")
caches.append(cache)
L是层数
对于输入的单个样本X,用参数w,b,从第1层,到第L层 前向走一遍。
(3)model_backward(AL, Y, caches)中的
# 第 L 层,激活函数是 Sigmoid
current_cache = caches[L-1]
grads["dA" + str(L-1)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation = "sigmoid")
# 前 L-1 层,激活函数是 ReLU
for l in reversed(range(L-1)):
current_cache = caches[l]
dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 1)], current_cache, activation = "relu")
grads["dA" + str(l)] = dA_prev_temp
grads["dW" + str(l + 1)] = dW_temp
grads["db" + str(l + 1)] = db_temp
注意 reversed(range(L-1)) 是从l开始到1 (从后往前),因为是反向传播,计算梯度
(4)在update_parameters(parameters, grads, learning_rate)中的
L = len(parameters) // 2 # 神经网络层数,包括输入层
for l in range(L):
parameters["W" + str(l+1)] -= learning_rate*grads["dW" + str(l+1)]
parameters["b" + str(l+1)] -= learning_rate*grads["db" + str(l+1)]
L是参数个数
对每个参数进行更新
(5)nn_model()中的
循环次数为:迭代次数
结束:可以看出DNN 并没有那么难,在熟悉DNN的数学原理后,代码是把数学过程呈现出来,当然呈现过程可能会有编程技巧,这就另说了。所谓调参,可以改nn_model()中的参数,比如300 与 1500次迭代,训练处的模型准确度肯定不一样,具体定多少就要调了。