最大堆、最小堆详解

最大堆、最小堆详解

Overview

最大堆和最小堆是二叉堆的两种形式。二叉堆(binary heap)是一种特殊的堆，二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足堆特性：父节点总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。

一、二叉堆

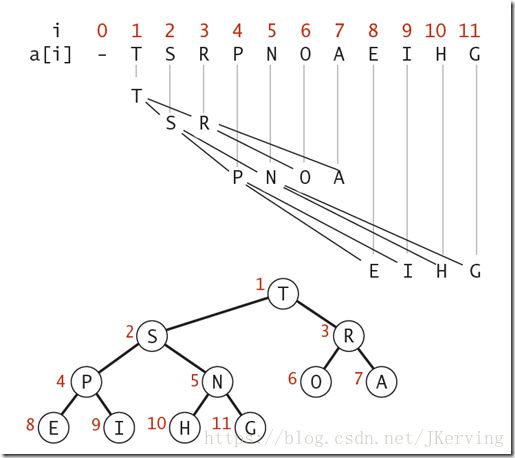
二叉堆的表现形式：我们可以使用数组的索引来表示元素在二叉堆中的位置。

从上图中可以得出：

• 元素k的父节点所在数组中的位置为[k/2]
• 元素k的子节点所在数组中的位置为2k和2k+1
• 假设堆有n个节点，树的高度为h=floor(logn)

根据以上规则，我们可以使用二维数组来表示二叉堆。

二、最大堆、最小堆详解

对于最大堆来说，最大元素位于根节点，那么删除操作就是交换根节点与堆的最后一个节点，然后将交换后的最后一个节点(交换前为根节点，value为最大值)移除并返回元素。此时新根节点需要下沉到适合的位置；当插入新元素的时候，将新元素添加至二叉堆的最后一个节点后，此时新节点需要根据value进行上浮操作，直到找到适合的位置。

最小堆和最大堆完全相反，最小元素位于根节点，下沉、上浮操作和最大堆基本相同。

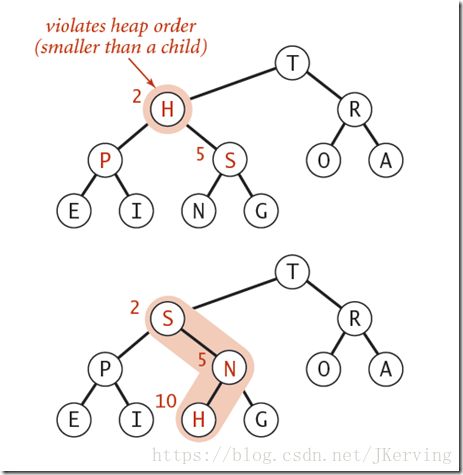
(以最大堆为例)由上至下的下沉建堆操作

​ 当某一节点比其子节点要小时，根据最大堆的定义，我们需要和其子节点中较大的子节点进行交换以重新建堆，直到该节点都大于其子节点为止。

source code：

private static void Sink(int k){
    while(2*k<N){
        int j = 2*k;
        if(H[j].CompareTo(H[j+1])<0)
            j++;
        if(H[k].CompareTo(H[j])>0)
            break;
        Swap(H,k,j);
        k=j;
    }
}

根据下沉(Sink)操作，可以推出：移除并返回最大元素操作DelMax为：

1. 交换最后一个元素和根节点元素
2. 对新根节点从上至下进行下沉动作，重新建堆
3. 将最后一个元素置空

实现如下：

public static T DelMax()
{
    //根元素从1开始，0不存放值
    T max = pq[1];
    //将最后一个元素和根节点元素进行交换
    Swap(H, 1, N--);
    //对根节点从上至下重新建堆
    Sink(1);
    //将最后一个元素置为空
    H[N + 1] = default(T);
    return max;
}

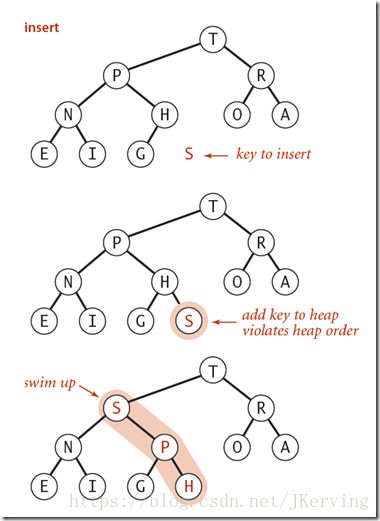
(以最大堆为例)由下至上的上浮建堆操作

如果一个节点的值大于其父节点的值，那么该节点需要上移，一直到满足该节点大于其两个子节点，而小于其根节点为止，从而达到使整个堆实现二叉堆的要求。

由上图可以看到，我们只需将该元素k和其父元素k/2进行比较，如果比父元素大，则交换，然后迭代，一直到比父元素小为止。

实现如下：

private static void Swim(int k)
{
    //如果元素比其父元素大，则交换
    while (k > 1 && H[k].CompareTo(H[k / 2]) > 0)
    {
        Swap(H, k, k / 2);
        k = k / 2;
    }
}

根据上浮操作，可以得知，对于最大堆的插入操作变为将该元素从下往上上浮，重新建堆操作：

1. 将新元素添加至最大堆最后一个节点后
2. 该元素进行从下至上的上浮动作
   

实现如下：

public static void Insert(T s)
{
    //将元素添加到数组末尾
    H[++N] = s;
    //然后让该元素从下至上重建堆
    Swim(N);
}

未完待续…