leetcode--统计全 1 子矩形

 题目是LeetCode第196场周赛的第三题，链接：1504. 统计全 1 子矩形。具体描述：给你一个只包含0和1的rows * columns矩阵mat，请你返回有多少个子矩形的元素全部都是1。

 示例1：

输入：mat = [[1,0,1],
            [1,1,0],
            [1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

 示例2：

输入：mat = [[0,1,1,0],
            [0,1,1,1],
            [1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。

 示例3：

输入：mat = [[1,1,1,1,1,1]]
输出：21

 示例4：

输入：mat = [[1,0,1],[0,1,0],[1,0,1]]
输出：5

 这道题的做法就是枚举以坐标(i,j)为右下角的话有多少个全1矩阵。首先需要做一些预处理，统计每一行上每个位置上在竖方向上有多少个连续的1，所以把经过预处理后的每一行看做一个柱状图的话，每个柱子的高度就代表了这一列有多少个连续的1（以这一列的1为底）。然后要计算全1矩阵的话就会方便很多，因为限定了以(i,j)为右下顶点，所以只需要我们枚举可能的宽度（最小是1，最大是此行到(i,j)为止最长连续1的长度），在每个可能的宽度上，根据可能的最小高度h（就是这个宽度范围内所有柱子的最小高度），可以得到h个全1矩阵（其实就是高分别为1、2、…、h一共h种），累加到结果上即可。假设行数为m，列数为n，则时间复杂度为$O(m{n}^2)$，空间复杂度为$O(1)$。

 JAVA版代码如下：

class Solution {
    public int numSubmat(int[][] mat) {
        int row = mat.length, col = mat[0].length;
        for (int i = 1; i < row; ++i) {
            for (int j = 0; j < col; ++j) {
                if (mat[i][j] == 0) {
                    continue;
                }
                mat[i][j] = mat[i - 1][j] + 1;
            }
        }
        int result = 0;
        for (int i = 0; i < row; ++i) {
            for (int j = 0; j < col; ++j) {
                if (mat[i][j] == 0) {
                    continue;
                }
                int minHeight = mat[i][j];
                int left = j;
                while (left >= 0 && mat[i][left] > 0) {
                    minHeight = Math.min(minHeight, mat[i][left--]);
                    result += minHeight;
                }
            }
        }
        return result;
    }
}

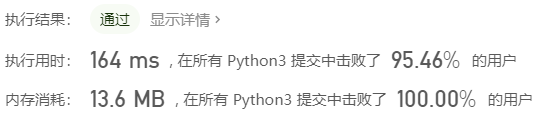
 提交结果如下:

 Python版代码如下：

class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:
        height = mat#copy.deepcopy(mat)
        row, col = len(mat), len(mat[0])
        for i in range(1, row):
            for j in range(col):
                if height[i][j] == 1:
                    height[i][j] = height[i - 1][j] + 1
        result = 0
        for i in range(row):
            for j in range(col):
                if height[i][j] == 0:
                    continue
                left = j
                minHeight = height[i][j]
                while left >= 0 and height[i][left] > 0:
                    result += minHeight
                    left -= 1
                    minHeight = min(minHeight, height[i][left])
        return result

 提交结果如下:

 另外还可以通过单调栈省去上面算法需要往前回溯统计矩阵数的步骤，将时间复杂度将为$O(mn)$，空间复杂度则升为$O(n)$。具体解释见这里或者代码注释。

 JAVA版代码如下：

class Solution {
    public int numSubmat(int[][] mat) {
        int row = mat.length, col = mat[0].length;
        for (int i = 1; i < row; ++i) {
            for (int j = 0; j < col; ++j) {
                if (mat[i][j] == 0) {
                    continue;
                }
                mat[i][j] = mat[i - 1][j] + 1;
            }
        }
        int result = 0;
        for (int i = 0; i < row; ++i) {
            Stack stack = new Stack<>();
            int cursum = 0;
            for (int j = 0; j < col; ++j) {
                if (mat[i][j] == 0) {
                    stack = new Stack<>();
                    cursum = 0;
                    continue;
                }
                if (stack.empty() || mat[i][j] > stack.peek()[0]) {
                    stack.push(new int[] {mat[i][j], 1});
                    cursum += mat[i][j];
                    result += cursum;
                }
                else {
                    int curWidth = 1;
                    while (!stack.empty() && stack.peek()[0] >= mat[i][j]) {
                        int[] hw = stack.pop();
                        curWidth += hw[1];
                        cursum -= (hw[0] - mat[i][j]) * hw[1];
                    }
                    stack.push(new int[] {mat[i][j], curWidth});
                    cursum += mat[i][j];
                    result += cursum;
                }
            }
        }
        return result;
    }
}

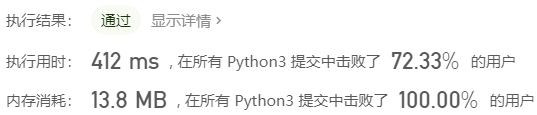
 提交结果如下:

 Python版代码如下：

class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:
        height = mat
        row, col = len(mat), len(mat[0])
        for i in range(1, row):
            for j in range(col):
                if height[i][j] == 1:
                    height[i][j] = height[i - 1][j] + 1
        result = 0
        for i in range(row):
            # 高递增的单调栈，存放[高，宽]
            stack = []
            # 累加前面的全1矩阵数
            cursum = 0
            for j in range(col):
                if height[i][j] == 0:
                    stack = []
                    cursum = 0
                    continue
                if not stack or height[i][j] > stack[-1][0]:
                    # 当前高度大于之前的最大高度的话
                    # 那么以当前点为右下角的全1矩阵数就是cursum+当前高度
                    # 其中cursum代表了宽度为2、3...的全1矩阵数
                    stack.append([height[i][j], 1])
                    cursum += height[i][j]
                    result += cursum
                else:
                    # 当前高度比之前的最大高度低的话
                    # 比当前高度高的那些都失去了对后面的影响，需要去掉
                    # 只留下一个更宽的以当前高度为高的矩形
                    curWidth = 1
                    while stack and stack[-1][0] >= height[i][j]:
                        h, w = stack.pop()
                        curWidth += w
                        # 因为将这些更高的高度降至跟当前高度一样
                        # 在这过程中失去的那些全1矩阵数需要减掉
                        cursum -= (h - height[i][j]) * w
                    stack.append([height[i][j], curWidth])
                    cursum += height[i][j]
                    result += cursum
        return result

 提交结果如下: