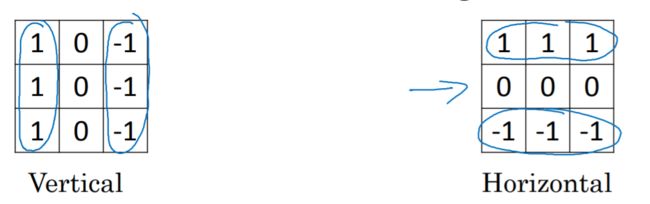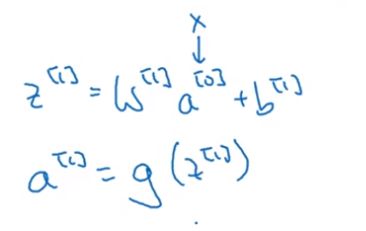吴恩达卷积神经网络课程——第一周笔记
Week 1
目录
Week 1
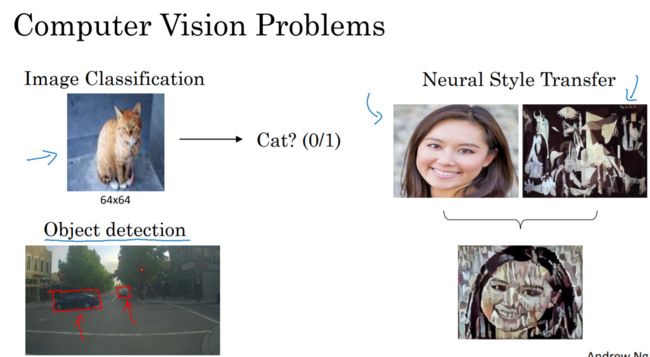
1-1、计算机视觉
1-2、边缘检测示例
1-3、更多关于边缘检测内容
1-4、Padding
1-5、卷积步长
1-6、卷积为何有效
1-7、单层卷积网络
1-8、简单卷积网络示例
1-9、池化层
1-10、卷积神经网络示例
1-11、为什么使用卷积?
1-1、计算机视觉
1-2、边缘检测示例
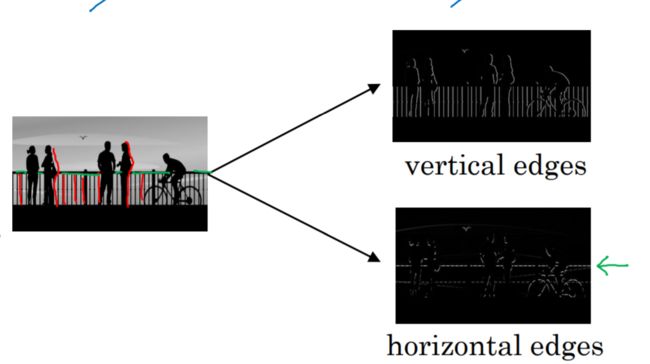
卷积运算就是卷积神经网络最基本的组成部分,在这里用边缘检测示例讲解卷积运算。给一张图片,要让电脑搞清楚图片里面有什么,做的第一件事就是检测图片中的垂直边缘(vertical edges):比如说这张图片里的栏杆、人的轮廓等,然后也要检测水平边缘(horizontal edges):比如水平的栏杆等。
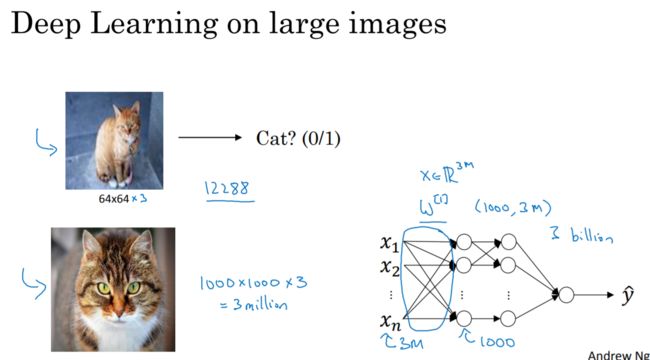
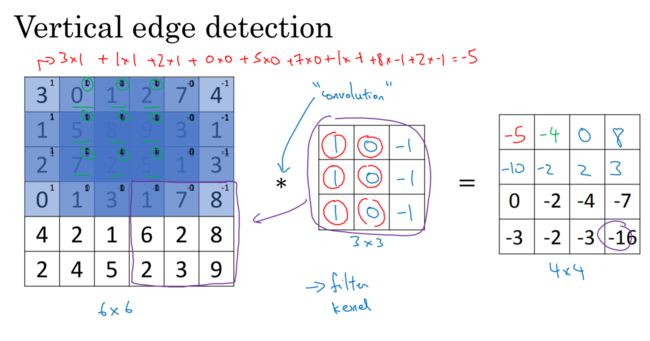
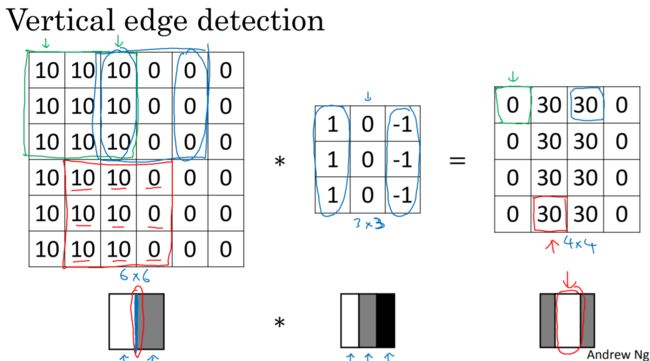
那么问题来了,如何在图片中检测这些边缘呢?举个例子:给个6×6的灰度图像,因为他是灰度图像,所以它实际就是个6×6×1的矩阵(而不是6×6×3的,一位没有RGB三个通道)。我们会构造一个3×3的过滤器和这个6×6的矩阵进行卷积运算。那么这个卷积运算的输出,会得到一个4×4的矩阵,也可以把她看成一个4×4的图像。输出为什么是4×4的呢?
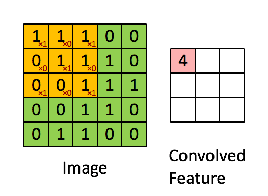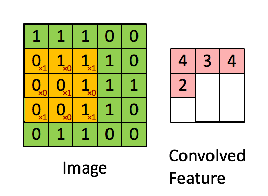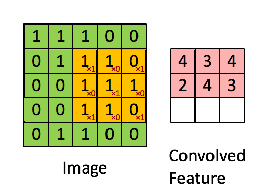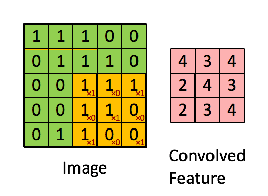
卷积运算就是从图像的左上角开始,用一个过滤器(像这个例子中的3×3的过滤器),图像与过滤器对应起来相乘再相加,并用计算结果代替输出结果的左上角第一个的值。然后,过滤器向右移动一列,并作同样的运算。以此类推,从左到右、从上到下,即可得到一幅新图像。下图为一些卷积运算的动图:
为什么这个能做垂直边缘检测器呢?看个例子:
输入为左边一半10,右边一半0,代表的图像大概是白+灰(0代表黑,255代表白)然后经过卷积运算,得到的结果是中间白,左右两边灰,中间白色区域就是说明表示在图像中间有个特别明显的 垂直边缘。
1-3、更多关于边缘检测内容
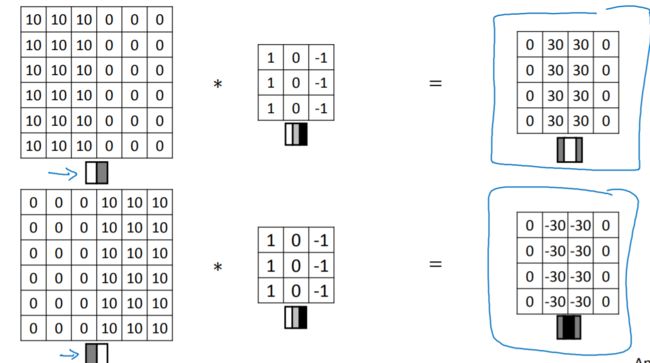
当数字反转时,输出结果也会发生相应的变化。
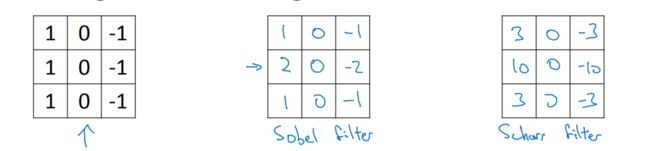
也许会很好奇,为什么垂直滤波器中的数字是这几个,能不能换其他数字?答案是可以的,例如:以下都是垂直滤波器。
水平滤波器就是把垂直滤波器翻转90°:
1-4、Padding
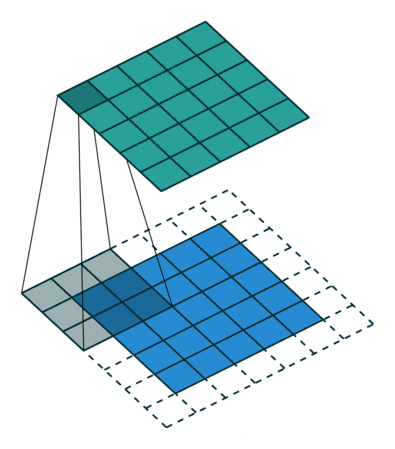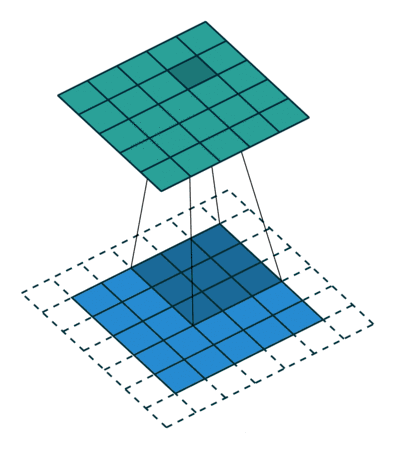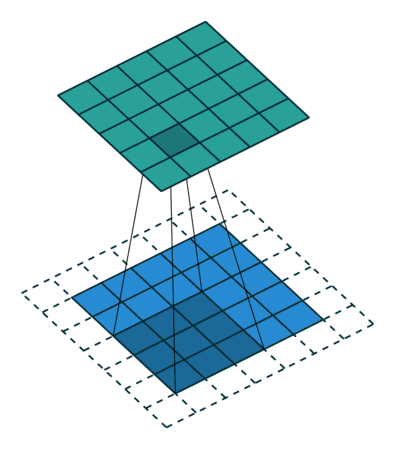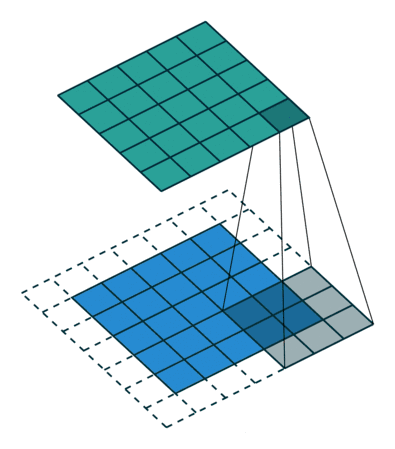
为了构建深度神经网络,我们需要做的一个基本的卷积操作就是Padding。在上面,我们知道:3×3的过滤器和这个6×6的矩阵进行卷积运算,那么这个卷积运算的输出,会得到一个4×4的矩阵。但是我们发现,这样的话,每次检测完边缘特征,图片就缩小了,所以到后期图片可能变得很小了,这是第一个缺点。第二个缺点是,我们发现,用过滤器与图片进行卷积运算时,位于角落的像素,过滤器只经过一次,而像其他中间的像素值,过滤器会有好几次经过他,这就说明那些角落的像素值在输出中采用较少,意味着你丢掉了图像的边缘位置的许多信息。
为了解决以上两个缺点:输出缩小和图像边缘大部分信息丢失。所以引进了Padding,也就是扩充边缘,也就是说,在刚开始时,我们给图片填充一层像素(用0填充),按之前例子来说,就在6×6的图像边缘加上一层像素,就变成了8×8的图像。如果再用3×3的卷积进行运算,那么输出结果就不是4×4的矩阵,而是6×6的矩阵,也就意味着输入输出大小不变了。
output size:
N: 输入的维度
F:卷积核大小
stride: 步长
有pad:扩充边缘的情况之下,pad的取值:
pad的作用就是保持全尺寸输出,不会改变图片大小。
有pad时计算output size:
()
1-5、卷积步长
N: 输入的维度
F:卷积核大小
stride: 步长
pad: 扩充边缘
()当商不是一个整数时就向下取整
1-6、卷积为何有效
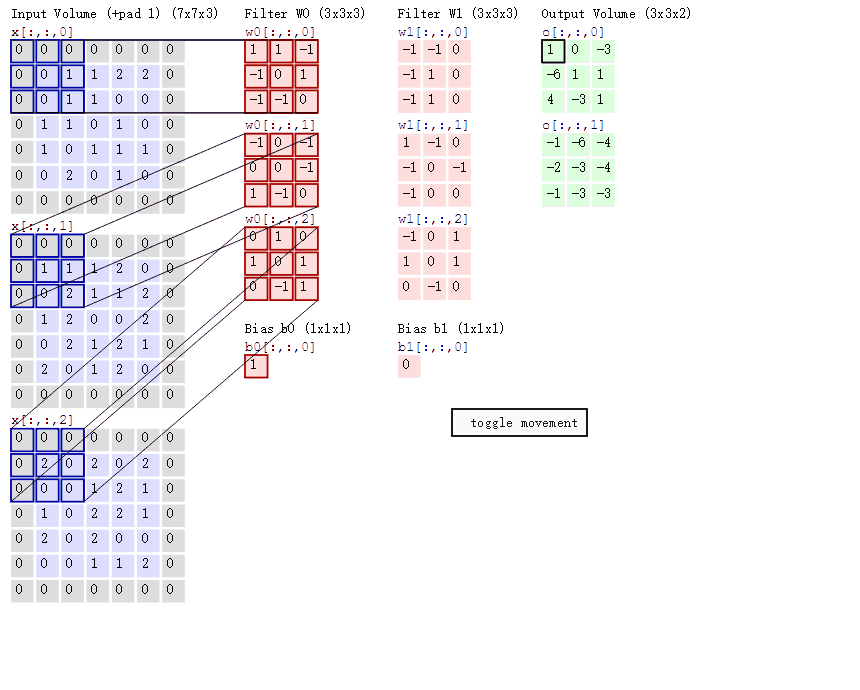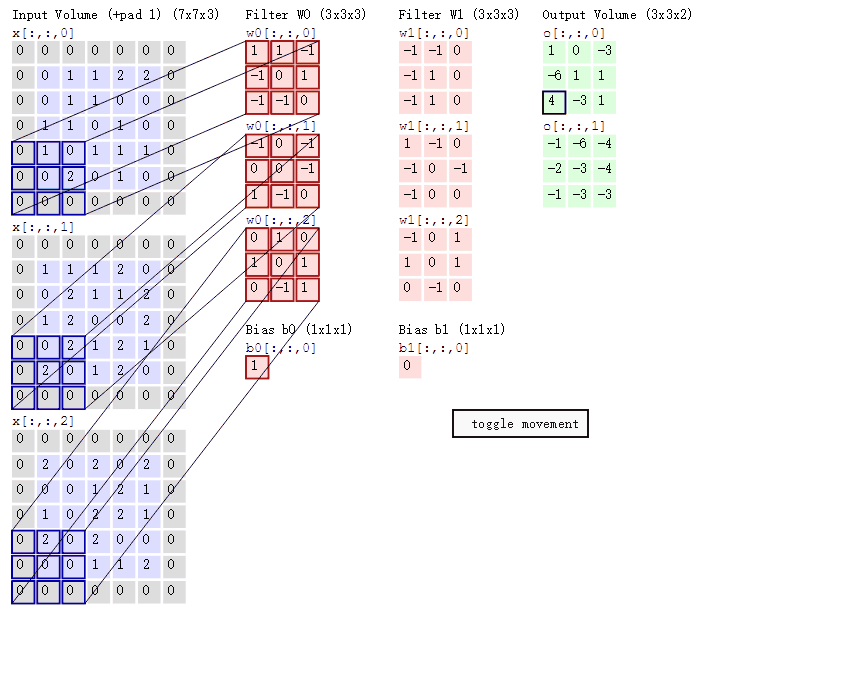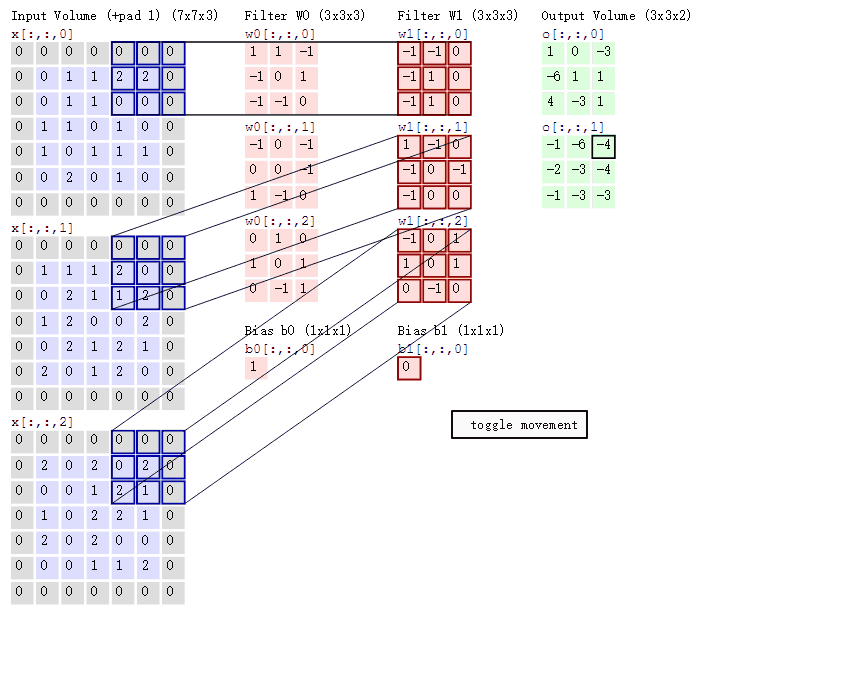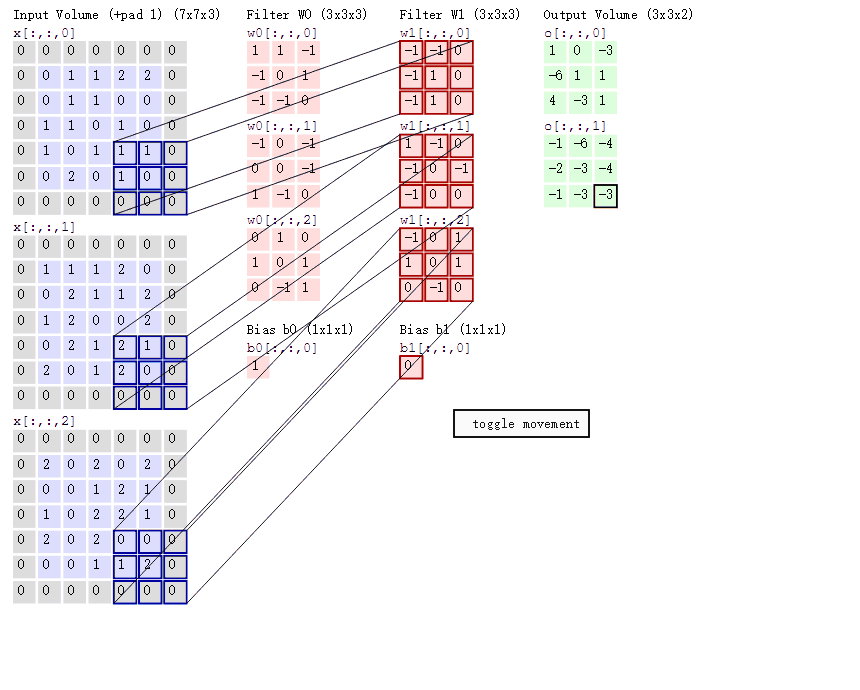
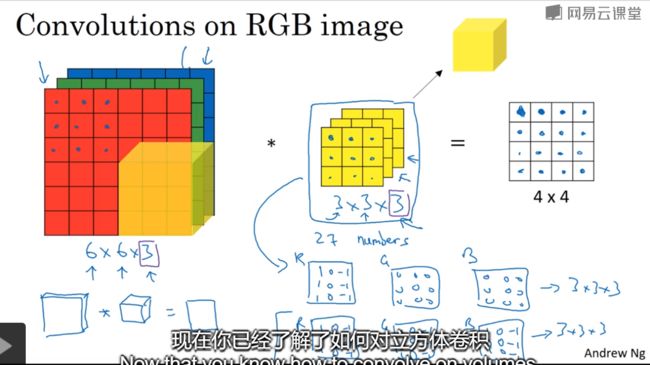
通过前面的知识,我们已经知道了如何对二维图像做卷积了,现在我们要学习的是在三维立体上做卷积——Converlutional on RGB images
下图就是在三维图像上做卷积运算:6×6×3,其中3代表通道数RGB,过滤器为3×3×3,3代表通道数,最后的输出为4×4的矩阵。
如果想只检测红色通道的特征,那就让过滤器的G、B通道均为0。
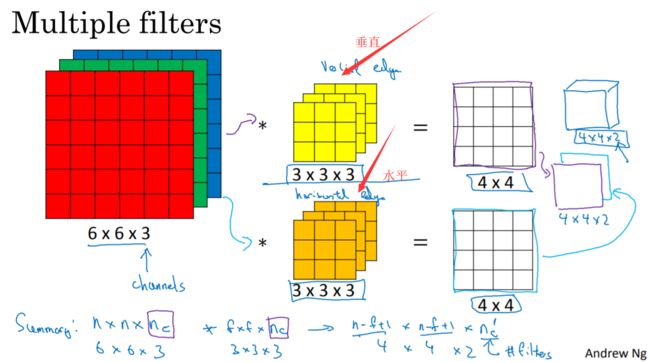
如果想要获得垂直边缘和水平边缘,那就分别用两种过滤器,然后将卷积后的结果结合在一起,结果就变成了4×4×2的矩阵。
总结:输入的图片为n×n×n1,过滤器为f×f×n1,其中n1就是通道数。结果为(n-f+1)×(n-f+1)×n2,其中n2为卷积核的个数
1-7、单层卷积网络
这节的内容是如何构建卷积神经网络的卷积层。上节课我们已经学会:如何通过两个过滤器(两个过滤器就是两个特征),卷积处理一个三维图像,并且输出两个4×4的矩阵。
我们之前在神经网络的前向传播中学过:
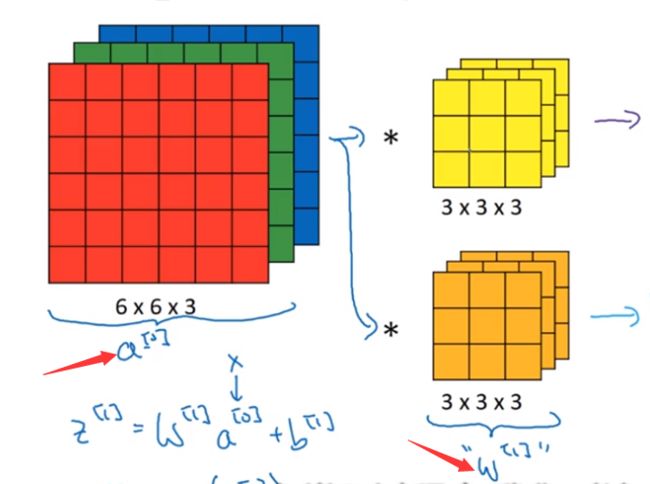
在这里,我们将输入图片也就是6×6×3的图片看成a[0] (x),将两个过滤器看成w[1],那么我们的输出结果4×4的矩阵就是w[1]×a[0],再对两个4×4的矩阵加上偏差,分别是b1、b2,最后再应用非线性函数relu,再把这两个叠在一起成为4×4×2矩阵,那么它(4×4×2的矩阵)就成为了神经网络的下一层,也就是激活层,也就是a[1],上述过程就体现了a[0]到a[1]的过程。总结流程就是:首先执行线性函数,然后所有元素相乘做卷积,再加上偏差,然后应用激活函数relu。这样就把一个6×6×3的a[0]变成了一个4×4×2的a[1]
练习:
一些符号规定:
1-8、简单卷积网络示例
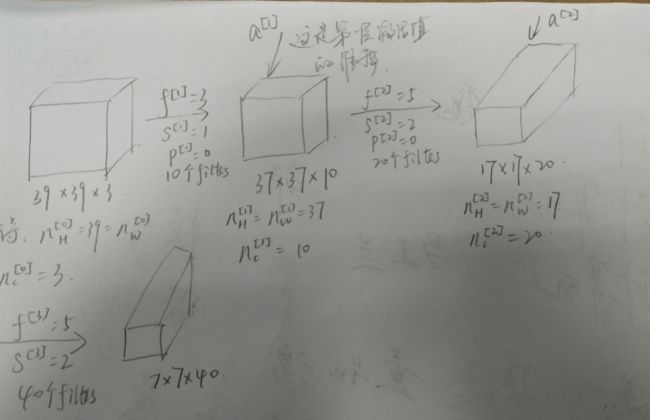
上节我们学了如何为卷积网络构建一个卷积层。现在来看一个深度卷积网络的具体示例。
经过以上图所示,到此,这张39×39×3的图像就处理完毕了,结果是再图片中提取了7×7×40=1960个特征。
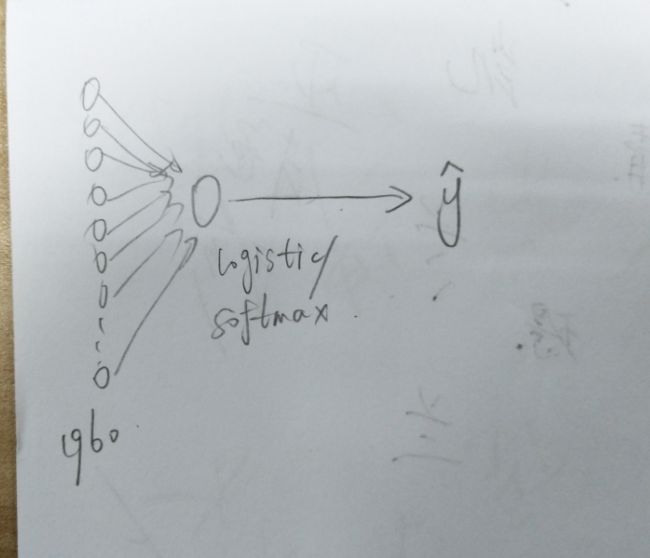
然后对该卷积层进行处理可以将其展开成1960个单元,也就是把他展成一个向量,其填充内容是logistic回归或是softmax回归,最后用y_hat来表示神经网络的预测输出。
设计神经网络时,确定这些超级参数比较费工夫,比如说:步长,padding,过滤器的大小,以及多少个过滤器等等。
一个典型的卷积网络通常由三层:卷积层(convolution或者Conv)、池化层(Pooling)、全连接层(Fully connected或者FC)
1-9、池化层
除了卷积层,卷积网络也经常使用池化层来缩减模型的大小,提高计算速度。同时提高所提取特征的鲁棒性。先看个池化层的例子:
输入为4×4的矩阵,用到的池化类型是最大池化(max pooling),输出结果是一个2×2的矩阵:
![]()
来看执行过程:把4×4的矩阵分成不同的区域,如图中的四种颜色区域,对于2×2的输出,输出的每个元素都是其对应颜色区域中的最大元素值。如下图所示。我们可以把这4×4的区域看成是某些特征的集合。
![]()
我们来看一个由若干个超级参数的示例,输入是一个5×5的矩阵我们采用最大池化法,他的过滤器的参数为3×3,步幅为1,输出矩阵是3×3: 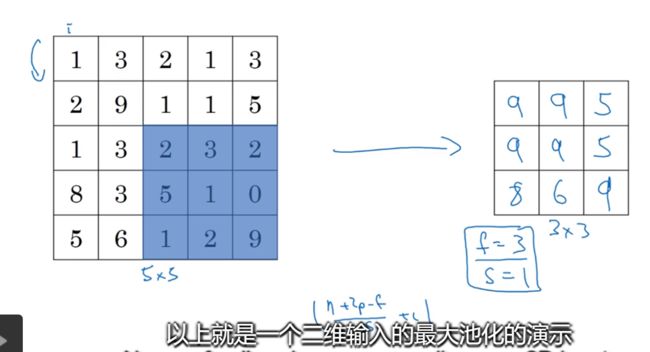
还有一种池化叫平均池化,选取的不是过滤器的最大值,而是平均值:
![]()
超级参数的常用值:f=2;s=2效果相当于高度和宽度缩减一半。最大池化时,往往很少用到padding
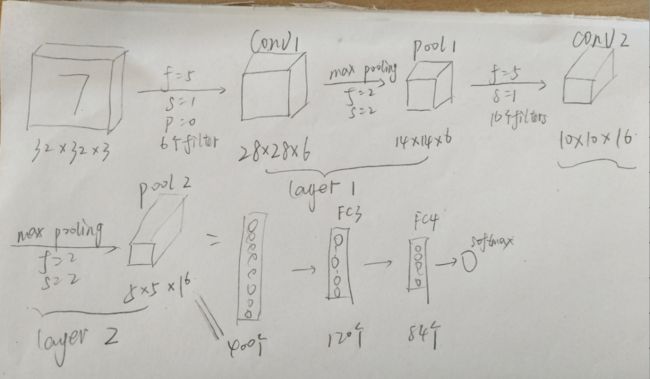
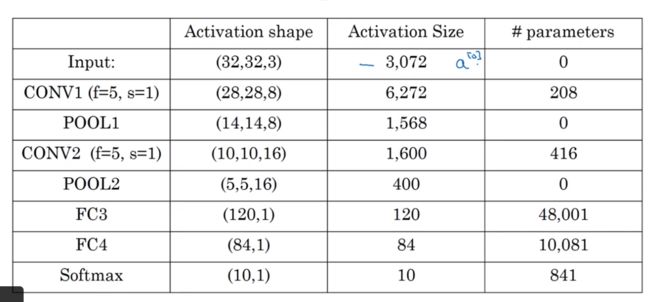
1-10、卷积神经网络示例
池化层和最大池化层没有参数,卷积层的参数较少,大多数参数都存在于全连接层中。随着神经网络的加深,激活值会逐渐变小。
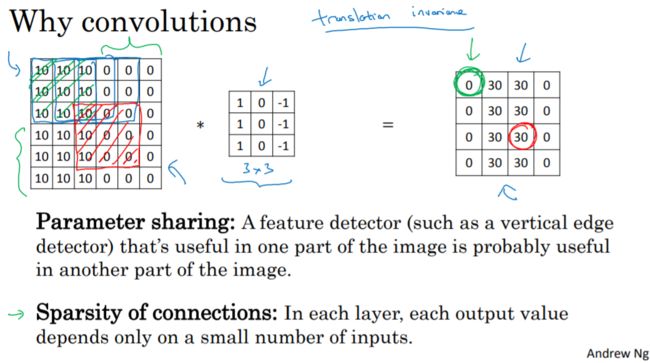
1-11、为什么使用卷积?
和只用全连接层相比,卷积层的两个优势在于参数共享和稀疏连接。