牛客算法周周练15题解
A:数列下标
题目描述
给出一个数列 A,求出一个数列B.
其中Bi 表示 数列A中 Ai 右边第一个比 Ai 大的数的下标(从1开始计数),没有找到这一个下标 Bi 就为0
输出数列B
输入描述:
第一行1个数字 n (n ≤ 10000)
第二行n个数字第 i 个数字为 Ai (0 ≤ Ai ≤ 1000000000)
输出描述:
一共一行,第 i 个数和第 i+1 个数中间用空格隔开.
示例1
输入
6
3 2 6 1 1 2
输出
3 3 0 6 6 0
说明
样例不用解释
水题,直接敲吧a…
#includeB:可持久化动态图上树状数组维护01背包
题目描述
你有一个长度为 n 序列 {a}(序列下标从1开始) ,每次可以从任意位置 i 花费 ai*i 的代价来把 ai 删除。
注意,删除后 ai 后面的数会依次向前补上(下标 -1 ) 。
求把整个序列删完的最小代价。
输入描述:
第一行一个整数 n ,第二行 n 个整数代表该序列。
输出描述:
一行一个整数表示删完序列的最小代价。
示例1
输入
2
3 2
输出
5
备注:
1<=n<=10^6 , |ai|<=10^7
保证答案在 (-2^64, 2^64) 范围内
大wu…整的花里胡哨,直接模拟QAQ(贪心)
删除数的时候,先删除负数,为保证ans尽可能的小,删负数的时候肯定是从后往前删除(不影响前面的负数的下标),我们发现此时负数刚好是ai * i
删完负数,正数从前往后删除即可,这样下标一直是1,代价就是正数本身。
#include C:璀璨光滑
#includeD:树上求和
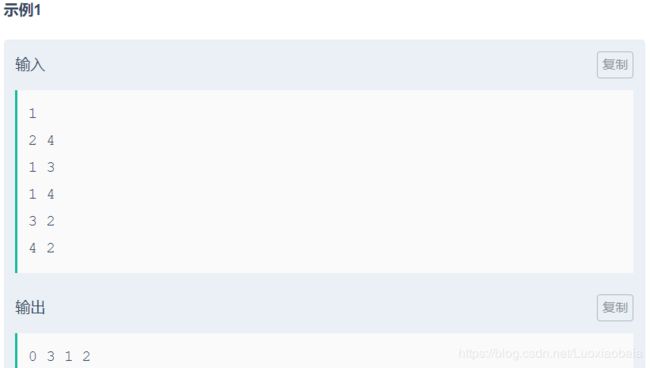
题目描述
给你一棵根为1的有N个节点的树,以及Q次操作。
每次操作诸如:
1 x y:将节点x所在的子树的所有节点的权值加上y
2 x:询问x所在子树的所有节点的权值的平方和,答案模23333后输出
输入描述:
第一行两个整数N,Q
第二行N个整数,第i个表示节点i的初始权值
接下来N-1行每行两个整数u,v,表示u和v之间存在一条树边
接下来Q行每行一个操作,格式如题目描述
输出描述:
对于每个询问操作,输出一行一个整数,表示答案在模23333后的结果
示例1
输入
5 5
0 0 0 0 0
1 2
1 3
3 4
3 5
1 1 3
1 3 7
1 4 5
1 5 6
2 1
输出
599
两个模板的结合,额外支持区间乘操作。
#include E:算式子
#include