Thinking in SQL系列之五：数据挖掘K均值聚类算法与城市分级

原创： 牛超   2017-02-21   Mail：[email protected]

引言：前一篇文章开始不再介绍简单算法，而是转到数据挖掘之旅。感谢CSDN将我前一篇机器学习C4.5决策树算法的博文推送到了首页，也非常荣幸能够得到云和恩墨的盖老师的肯定。个人会继续以精品博文分享我的观点，也希望结交更多的数据库、数据分析领域的朋友。

从前面几篇可以看到，SQL做为一种编程语言，能够满足各类数据处理的需要，关键就在于算法与思维方式。个人经常调侃SQL思考问题比大部分流行的开发语言多一个维度，因为SQL主要是二维思考（集合）、区别于一维（数据结构）的思维方式。对于ORACLE，通过以SQL（相对宏观）为主体、PLSQL（微观）为辅助，注入算法（灵魂），贯彻性能优化（章程），数据的价值能够充分有效发挥。

聚类问题，就是给定一个元素集合D，其中每个元素具有n个可观察属性，使用某种算法将D划分成k个子集，要求每个子集内部的元素之间相异度尽可能低，而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。本文将介绍聚类的经典算法K均值聚类算法，即K-MEANS，是一种观察类学习，通过以元素间的相异度迭代地划分簇并重新定位质心点重新聚类来达成的算法，找了如下的图以便加深理解。

算法本身较容易理解，但为了定量说明，还是先祭出几个数学公式

 用来定义两个元素，各自具有n个度量属性。

 用来标量X与Y的相异度（欧拉距离公式），本篇采用该公式。

 曼哈顿距离，即街区非直线段距离，很容易理解。也可以用来标量元素间相异度。

 标量规格化，为了平衡各个属性因取值单位不同对距离的影响而按比例映射到相同的取值区间。通常将各个属性均映射到[0,1]区间。

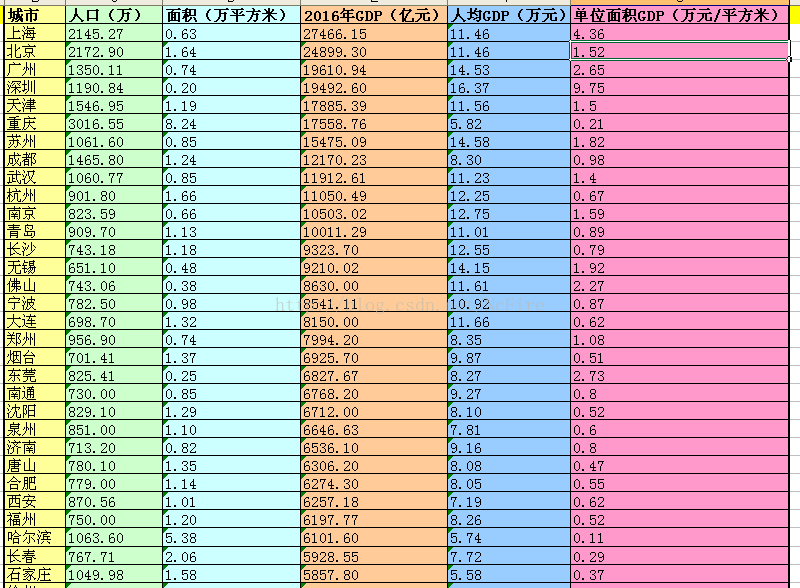
接着，我们来看看本次要用SQL实现的k-means算法示例：以2016年的GDP统计数据给中国城市分级：

目前这份是经个人简单加工的2016年真实国家统计数据，一共有100个城市的记录，共5个度量（人口、面积、年GDP、人均GDP、单位面积GDP)。

我们总是说不相信眼泪的北上广是一线城市，那么该如何给城市分成四线是个很有趣的问题，看了一下国家统计局的划分标准（此处省略1K字），但做为个人比较关心的是每个城市发达与市民富裕程度，于是简单地拍脑袋定义了如下模型：

X ={人口，人口密度，年GDP，人均GDP，单位面积GDP}，共5个维度，权重都是1;

每个度量属性a的标量规格化区间定义为[0,1];

聚合点相异度需要以质心点为基准计算，初始质心点取GDP名次的4等分点，简化为MOD(名次,21)=0;

元素相异度直接使用欧拉距离公式，即

准备工作：

1.定义表象性的业务表，即城市GDP数据表

--城市GDP
CREATE TABLE CITY_GDP_T
(
CITY VARCHAR2(100),--城市名
POPULATION NUMBER ,--人口
AREA NUMBER,--面积
GDP_YEAR NUMBER,--年GDP
GDP_PER_CAPITA NUMBER ,--人均GDP
GDP_PER_AREA NUMBER --单位面积GDP
);

2.加载数据后查询如下：

3.先预演一下质心点经过一次聚类后重新被选择的算法程序，其中第一代初始质心点根据GDP的分段城市的元素属性，TA1，再根据TA1的聚类点用算术平均法计算得到第二代质心点，SQL如下：

WITH TA AS --整理度量值
 (SELECT T.CITY,
         AREA,
         ROW_NUMBER() OVER(ORDER BY GDP_YEAR DESC) RNUM,
         --人口
         POPULATION,
         MIN(POPULATION) OVER() MIN_POPULATION,
         MAX(POPULATION) OVER() MAX_POPULATION,
         --人口密度
         ROUND(POPULATION / AREA, 2) POLA_PER_AREA,
         MIN(ROUND(POPULATION / AREA, 2)) OVER() MIN_POLA_PER_AREA,
         MAX(ROUND(POPULATION / AREA, 2)) OVER() MAX_POLA_PER_AREA,
         --年GDP
         GDP_YEAR,
         MIN(GDP_YEAR) OVER() MIN_GDP_YEAR,
         MAX(GDP_YEAR) OVER() MAX_GDP_YEAR,
         --人均GDP
         GDP_PER_CAPITA,
         MIN(GDP_PER_CAPITA) OVER() MIN_GDP_PER_CAPITA,
         MAX(GDP_PER_CAPITA) OVER() MAX_GDP_PER_CAPITA,
         --单位面积GDP
         GDP_PER_AREA,
         MIN(GDP_PER_AREA) OVER() MIN_GDP_PER_AREA,
         MAX(GDP_PER_AREA) OVER() MAX_GDP_PER_AREA
    FROM CITY_GDP_T T),
TB AS --规格化，以消除属性值单位不同造成的影响
 (SELECT CITY,
         RNUM,
         (POPULATION - MIN_POPULATION) / (MAX_POPULATION - MIN_POPULATION) POLA_VALUE, --人口 ，规格化到[0,1]区间
         (POLA_PER_AREA - MIN_POLA_PER_AREA) /
         (MAX_POLA_PER_AREA - MIN_POLA_PER_AREA) PPA_VALUE, --人口密码
         (GDP_YEAR - MIN_GDP_YEAR) / (MAX_GDP_YEAR - MIN_GDP_YEAR) GDP_VALUE, --GDP
         (GDP_PER_CAPITA - MIN_GDP_PER_CAPITA) /
         (MAX_GDP_PER_CAPITA - MIN_GDP_PER_CAPITA) GPC_VALUE, --人均GDP 
         (GDP_PER_AREA - MIN_GDP_PER_AREA) /
         (MAX_GDP_PER_AREA - MIN_GDP_PER_AREA) GPA_VALUE --单位面积GDP
    FROM TA
  --where mod(rnum,10) = 5
  ),
TA1 AS --第一代质心点选择，根据GDP
 (SELECT RNUM       CLUSTERID,
         POLA_VALUE POLA_CENTROID,
         PPA_VALUE  PPA_CENTRIOID,
         GDP_VALUE  GDP_CENTROID,
         GPC_VALUE  GPC_CENTROID,
         GPA_VALUE  GPA_CENTROID
    FROM TB
   WHERE TB.RNUM > 0
     AND MOD(TB.RNUM, 21) = 0 --选质心点，利用GDP值
  ),
TC AS
 (SELECT A.CLUSTERID,
         B.CITY CTB,
         B.RNUM CTB_ROW,
         B.POLA_VALUE,
         B.GDP_VALUE,
         B.GPC_VALUE,
         B.GPA_VALUE,
         SQRT(POWER(B.POLA_VALUE - A.POLA_CENTROID, 2) +
              POWER(B.GDP_VALUE - A.GDP_CENTROID, 2) +
              POWER(B.GPC_VALUE - A.GPC_CENTROID, 2) +
              POWER(B.GPA_VALUE - A.GPA_CENTROID, 2)) DVALUE --欧拉距离
    FROM TA1 A
   CROSS JOIN TB B),
TD AS
 (SELECT TC.*,
         ROW_NUMBER() OVER(PARTITION BY CTB_ROW ORDER BY DVALUE) SUB_RNUM
    FROM TC),
TE AS --聚类选择，各元素取相异度最低的质心点
 (SELECT * FROM TD WHERE SUB_RNUM = 1),
TA2 AS --第二代质心点选择，根据各属性算术平均值
 (SELECT TE.CLUSTERID CLUSTERID,
         AVG(POLA_VALUE) POLA_CENTROID,
         AVG(GDP_VALUE) GDP_CENTROID,
         AVG(GPC_VALUE) GPC_CENTROID,
         AVG(GPA_VALUE) GPA_CENTROID
    FROM TE
   GROUP BY CLUSTERID)
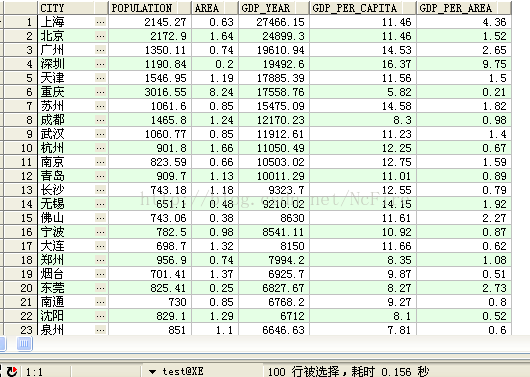
SELECT * FROM TA2

可以在集合TA1后面做一个SELECT看一下第一代的质心点，如下图：

执行SQL后看一下第二代的质心点，发现维值都发生了变化，说明质心点还是不稳定的，需要迭代地寻找下去。

通过上面的预演，脑子也做了预热。找到规律之后，霍然思路全部连通，K-MEANS聚类问题的关键就在于递归地寻找最稳定的质心点集合。为了保持算法的通用性，抽象出了如下8个维度的聚类训练集，同时定义了批次ID与初始质心标识（0，1）：

--K-MEANS聚类训练集
CREATE TABLE DM_KMEANS_LEANING_T
(
EID NUMBER ,--元素ID
ELABEL VARCHAR2(100),
BATCH_ID NUMBER ,
C1 NUMBER ,--维度1质心坐标 规格化后
C2 NUMBER ,
C3 NUMBER ,
C4 NUMBER ,
C5 NUMBER ,
C6 NUMBER ,
C7 NUMBER ,
C8 NUMBER ,
CENTRIOD_FLAG NUMBER(1)--初始质心 1/0
);
-- Create/Recreate indexes 
CREATE INDEX DM_KMEANS_LEANING_N1 ON DM_KMEANS_LEANING_T (BATCH_ID);

为了能够传入父代质心点集合得到子代集合，需要定义如下对象：

CREATE OR REPLACE TYPE DM_KMEANS_CENTROID_OBJ IS OBJECT
(
  CLUSTER_ID NUMBER, --簇ID
  C1         NUMBER, --维度1质心坐标 规格化后
  C2         NUMBER,
  C3         NUMBER,
  C4         NUMBER,
  C5         NUMBER,
  C6         NUMBER,
  C7         NUMBER,
  C8         NUMBER,
  GENERATION NUMBER  --子代数
); 
CREATE OR REPLACE TYPE DM_KMEANS_CENTROID_TAB IS TABLE OF DM_KMEANS_CENTROID_OBJ;

最重要的算法实现，考虑到ORACLE自定义函数本身是可递归的，我们便来实现这么一个质心点选择的递归函数，相异度选用欧拉距离公式，为了防止迭代次数过多影响性能，可以指定参数P_MAX_GENERATIOIN NUMBER，即最大递归子代数，具体脚本如下：

CREATE OR REPLACE FUNCTION FUN_DM_KMEANS_CENTROID(P_BATCH_ID NUMBER, --批次ID
                                                  P_MAX_GENERATIOIN NUMBER DEFAULT NULL ,--最大递归子代数
                                                  P_CENTRIOD_LIST DM_KMEANS_CENTROID_TAB DEFAULT NULL --质心点
                                                 )
  RETURN DM_KMEANS_CENTROID_TAB AS
  V_PARENT_LIST  DM_KMEANS_CENTROID_TAB; --本次迭代质心点 D
  V_CURRENT_LIST DM_KMEANS_CENTROID_TAB; --质心点计算结果 D'
  V_CNT          NUMBER;-- D'- D元素数
BEGIN
  --取质心点 D
  IF P_CENTRIOD_LIST IS NOT NULL THEN
    V_PARENT_LIST := P_CENTRIOD_LIST;
  ELSE
    SELECT DM_KMEANS_CENTROID_OBJ(EID, C1, C2, C3, C4, C5, C6, C7, C8, 1) BULK COLLECT
      INTO V_PARENT_LIST
      FROM DM_KMEANS_LEANING_T
     WHERE BATCH_ID = P_BATCH_ID
       AND CENTRIOD_FLAG = 1;
    IF P_MAX_GENERATIOIN = 1 THEN
      RETURN V_PARENT_LIST ;
    END IF ;
  END IF;
  --计算修正后的质心点 D'
  WITH TC AS --计算各点相对质心点相异度（笛卡尔集）
   (SELECT 
     A.CLUSTER_ID,
     A.GENERATION,
     B.EID CTB_ROW,
     B.C1,
     B.C2,
     B.C3,
     B.C4,
     B.C5,
     B.C6,
     B.C7,
     B.C8,
     SQRT(NVL(POWER(B.C1 - A.C1, 2), 0) + NVL(POWER(B.C2 - A.C2, 2), 0) +
          NVL(POWER(B.C3 - A.C3, 2), 0) + NVL(POWER(B.C4 - A.C4, 2), 0) +
          NVL(POWER(B.C5 - A.C5, 2), 0) + NVL(POWER(B.C6 - A.C6, 2), 0) +
          NVL(POWER(B.C7 - A.C7, 2), 0) + NVL(POWER(B.C8 - A.C8, 2), 0)) DVALUE --欧氏距离
      FROM TABLE(V_PARENT_LIST) A
      JOIN DM_KMEANS_LEANING_T B
        ON B.BATCH_ID = P_BATCH_ID),
  TD AS--相异度排名
   (SELECT TC.*,
           ROW_NUMBER() OVER(PARTITION BY CTB_ROW ORDER BY DVALUE) SUB_RNUM
      FROM TC),
  TE AS--聚类选择，各元素取相异度最低的质心点
   (SELECT * FROM TD WHERE SUB_RNUM = 1)
  SELECT DM_KMEANS_CENTROID_OBJ(TE.CLUSTER_ID,
                                AVG(C1), --平均值求新质心 C1维
                                AVG(C2),
                                AVG(C3),
                                AVG(C4),
                                AVG(C5),
                                AVG(C6),
                                AVG(C7),
                                AVG(C8),
                                GENERATION + 1 --子代+1
                                ) BULK COLLECT
    INTO V_CURRENT_LIST --生成D'
    FROM TE
   GROUP BY CLUSTER_ID, GENERATION;
   
   --判断最大子代限制条件
   IF P_MAX_GENERATIOIN IS NOT NULL AND V_CURRENT_LIST(1).GENERATION = P_MAX_GENERATIOIN THEN
     RETURN V_CURRENT_LIST;
   ELSE
    SELECT COUNT(1)
      INTO V_CNT
      FROM (SELECT C1, C2, C3, C4, C5, C6, C7, C8
             FROM TABLE(V_CURRENT_LIST)
            MINUS
            SELECT C1, C2, C3, C4, C5, C6, C7, C8
             FROM TABLE(V_PARENT_LIST) );
    IF V_CNT = 0 THEN
      RETURN V_CURRENT_LIST; --质心点集稳定后返回当前子代
    ELSE
      RETURN FUN_DM_KMEANS_CENTROID(P_BATCH_ID,P_MAX_GENERATIOIN, V_CURRENT_LIST); --递归计算质心点集
    END IF;
   END IF ;
END;

虽然是PLSQL，可以看到全篇没有用到循环，质心点的计算主体是面向集合的，其中TC是原始点集与质心点的笛卡尔集，投影列DVALUE相异度计算利用欧拉距离公式，推到TD中利用统计函数为每个质心点按相异度排名，TE取排名第一即相异度最小的组合，最后将质心点周围的点集的算术平均值做为新质心集合返回。全程的集合思维，即Thinking in SQL，如何使用？当然是SQL了，请往下看。

首先我们要把业务数据转换加载到训练集中，这是个简单的ETL过程，将城市GDP表数据经过抽取、维值[0,1]规格化转换、分配批次号3后最终加载到目标K-MEAN训练集：

INSERT INTO DM_KMEANS_LEANING_T
  (EID, ELABEL, BATCH_ID, C1, C2,C3,C4,C5,CENTRIOD_FLAG)
  WITH TA AS --整理度量值
   (SELECT T.CITY,
           AREA,
           ROW_NUMBER() OVER(ORDER BY GDP_YEAR DESC) RNUM,
           --人口
           POPULATION,
           MIN(POPULATION) OVER () MIN_POPULATION,
           MAX(POPULATION) OVER () MAX_POPULATION,
           --人口密度
           ROUND(POPULATION / AREA, 2) POLA_PER_AREA,
           MIN(ROUND(POPULATION / AREA, 2)) OVER() MIN_POLA_PER_AREA,
           MAX(ROUND(POPULATION / AREA, 2)) OVER() MAX_POLA_PER_AREA,
           --年GDP
           GDP_YEAR,
           MIN(GDP_YEAR) OVER() MIN_GDP_YEAR,
           MAX(GDP_YEAR) OVER() MAX_GDP_YEAR,
           --人均GDP
           GDP_PER_CAPITA,
           MIN(GDP_PER_CAPITA) OVER() MIN_GDP_PER_CAPITA,
           MAX(GDP_PER_CAPITA) OVER() MAX_GDP_PER_CAPITA,
           --单位面积GDP
           GDP_PER_AREA,
           MIN(GDP_PER_AREA) OVER() MIN_GDP_PER_AREA,
           MAX(GDP_PER_AREA) OVER() MAX_GDP_PER_AREA
      FROM CITY_GDP_T T),
  TB AS --规格化，以消除属性值单位不同造成的影响
   (SELECT CITY,
           RNUM,
           (POPULATION - MIN_POPULATION ) / (MAX_POPULATION - MIN_POPULATION) POLA_VALUE ,--人口 ，规格化到[0,1]区间
           (POLA_PER_AREA - MIN_POLA_PER_AREA ) / (MAX_POLA_PER_AREA - MIN_POLA_PER_AREA) PPA_VALUE ,--人口密码
           (GDP_YEAR - MIN_GDP_YEAR ) / (MAX_GDP_YEAR - MIN_GDP_YEAR) GDP_VALUE ,--GDP
           (GDP_PER_CAPITA - MIN_GDP_PER_CAPITA) / (MAX_GDP_PER_CAPITA - MIN_GDP_PER_CAPITA) GPC_VALUE,--人均GDP 
           (GDP_PER_AREA - MIN_GDP_PER_AREA) / (MAX_GDP_PER_AREA - MIN_GDP_PER_AREA) GPA_VALUE --单位面积GDP
      FROM TA
    ), -- ,
  TR1 AS
   (SELECT RNUM CLUSTERID,
           CITY,
           3 BATCH_ID,
           POLA_VALUE POLA_CENTRIOD,
           PPA_VALUE PPA_CENTRIOD,
           GDP_VALUE GDP_CENTRIOD,
           GPC_VALUE GPC_CENTROID,           
           GPA_VALUE GPA_CENTROID,
           CASE WHEN TB.RNUM > 0 AND MOD(TB.RNUM, 21) = 0 THEN 1 ELSE 0 END CENTRIOD_FLAG --选质心点，利用GDP值
      FROM TB)
  SELECT * FROM TR1 ;
  COMMIT ;

接着我们可以用这个批次ID来得到我们需要的稳定质心点，执行SQL很简单：

SELECT *
FROM TABLE( FUN_DM_KMEANS_CENTROID(3)) A  ;

通过计算结果，我们可以看到质心点在第10代(GENERATION)才得以稳定下来，如果想看看第5代长什么样怎么办？简单，如下：

SELECT *
FROM TABLE( FUN_DM_KMEANS_CENTROID(3,5)) A  ;

接下来我们回到问题的初衷，如何把城市分成四线，具体哪些城市是一线，只需要下面这一个SQL，和质心点选择函数中功能大同小异：

WITH PARAMS AS (
   SELECT 3 BATCH_ID , --批次ID
          NULL MAX_GENERATION--最大子代数 
   FROM DUAL 
   ) , TC AS
   (SELECT /*+ORDERED USE_NL(PM,A,B)*/ --HINT，引导选择正确执行计划
     A.CLUSTER_ID,
     A.GENERATION,
     SQRT(NVL(POWER(A.C1,2), 0) + NVL(POWER(A.C2,2), 0) + NVL(POWER(A.C3,2), 0) + NVL(POWER(A.C4,2), 0) 
     + NVL(POWER(A.C5,2), 0) + NVL(POWER(A.C6,2), 0) + NVL(POWER(A.C7,2), 0) + NVL(POWER(A.C8,2), 0) ) D_CLUSTER,--质点到原点欧拉距离,
     B.EID CTB_ROW,
     B.ELABEL ,
     B.C1,--人口
     B.C2,--人口密度
     B.C3,--年GDP
     B.C4,--人均GDP
     B.C5,--单位面积GDP
     B.C6,
     B.C7,
     B.C8,
     SQRT(NVL(POWER(B.C1,2), 0) + NVL(POWER(B.C2,2), 0) + NVL(POWER(B.C3,2), 0) + NVL(POWER(B.C4,2), 0) 
     + NVL(POWER(B.C5,2), 0) + NVL(POWER(B.C6,2), 0) + NVL(POWER(B.C7,2), 0) + NVL(POWER(B.C8,2), 0) ) D_EID,--元素点到原点欧拉距离,     
     SQRT(NVL(POWER(B.C1 - A.C1, 2), 0) + NVL(POWER(B.C2 - A.C2, 2), 0) +
          NVL(POWER(B.C3 - A.C3, 2), 0) + NVL(POWER(B.C4 - A.C4, 2), 0) +
          NVL(POWER(B.C5 - A.C5, 2), 0) + NVL(POWER(B.C6 - A.C6, 2), 0) +
          NVL(POWER(B.C7 - A.C7, 2), 0) + NVL(POWER(B.C8 - A.C8, 2), 0)) DVALUE --欧拉距离 质点到元素点欧拉距离
      FROM PARAMS PM
      CROSS JOIN TABLE( FUN_DM_KMEANS_CENTROID(PM.BATCH_ID , PM.MAX_GENERATION)) A
      JOIN DM_KMEANS_LEANING_T B
        ON B.BATCH_ID = PM.BATCH_ID),
  TD AS
   (SELECT TC.*,
           ROW_NUMBER() OVER(PARTITION BY CTB_ROW ORDER BY DVALUE) SUB_RNUM
      FROM TC)
  SELECT * FROM TD WHERE SUB_RNUM = 1
  ORDER BY D_CLUSTER DESC, D_EID DESC;

是不是和我一样迫不及待地想看结果了，我所关心的城市到底被分到了哪一级，输出结果:

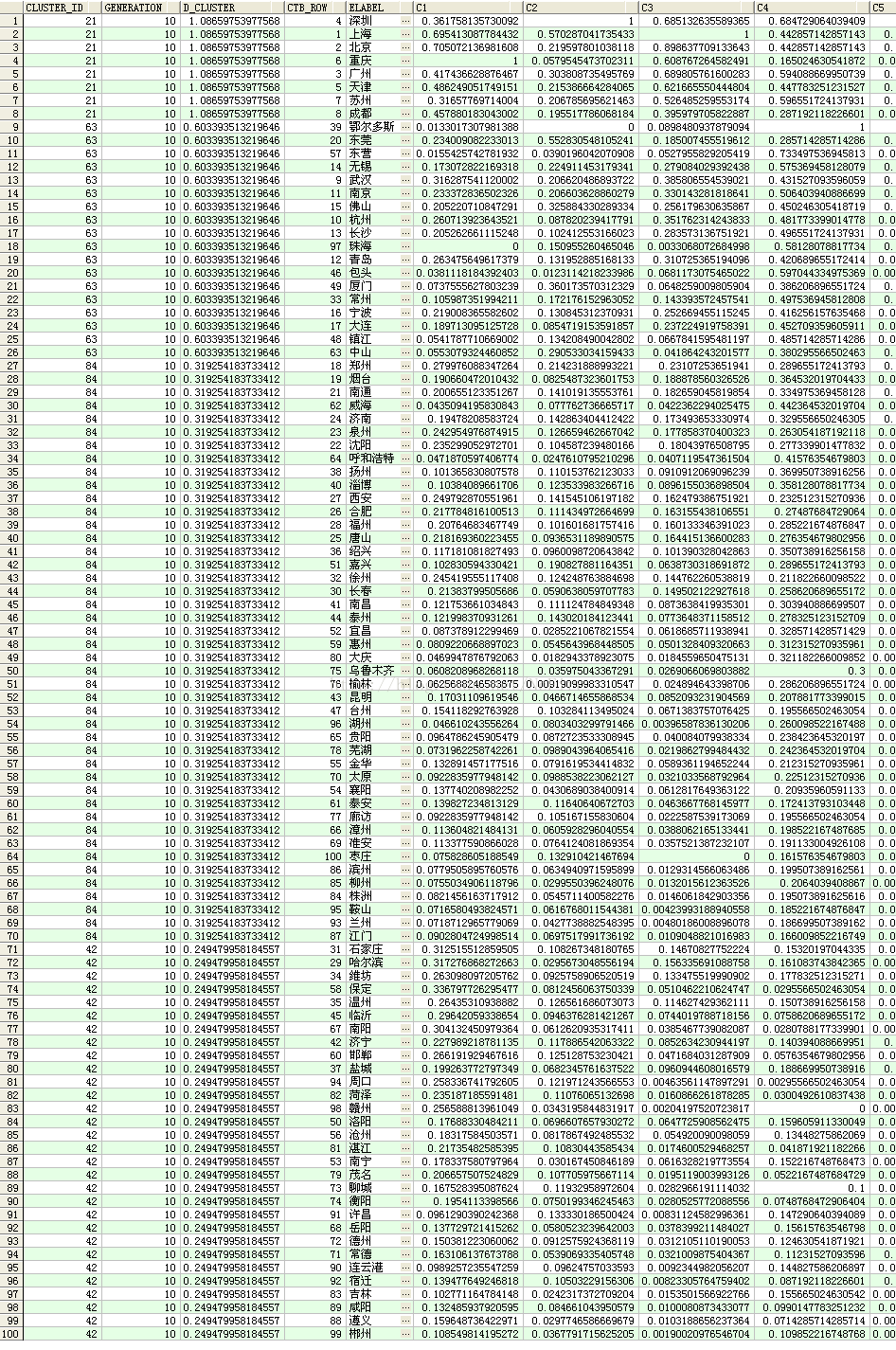
如此便计算出了我心目中的四线城市。对结果不喜的，莫争议，这就是个一个数字游戏，毕竟只是堆叠出来的度量模型没什么权威。简单分析一下，CUSTER_ID值的大小不能说明什么，只是用来给簇编号确定分类的。根据CLUSTER_ID分类，可以看到北上广深以及其他的直辖市都在最繁荣的分类中，苏州、成都能够挤进去说明很有实力。鄂尔多斯领跑二线。。。这个城市也很有趣。而我的家乡烟台只能搭上三线的边，难免有些失落。

至此，SQL版本的K-MEANS聚类算法已经介绍完，个人举的例子可能没有那么贴切。因为对数据挖掘来说，数据量太小，结果的偶然性会比较高。但麻雀虽小，却较为完整地用SQL表述了K-MEANS聚类的思想。实现这么个算法，全篇没有用到一个循环处理，还是那句话，数据处理，SQL为王。Thinking in SQL，处处是集合，或许，只有你想不到的。