《深入理解计算机系统》学习笔记(一)信息的表示和处理
引言
《深入理解计算机系统》这本书在IT界饱受欢迎。它内容广博,内涵丰富,全是干货,价值极高。好的程序员和一般的程序员,很大程度上就区别在他/她是否能写出高质量的,易读的,容错性强的代码。由于本人也是初学者,在这里希望能够通过做笔记的形式,和大家一起先大致阅读一遍这本书。
做一百件事,不如认真做好一件事
第二章 信息的表示和处理
万丈高楼平地起,信息的表示和处理是计算机系统的核心内容,是往后任何知识的基础。这一章大概要学这么几个东西:
- 信息存储
- 整形表征
- 整形运算
- 浮点数
一、信息存储
比特(bit) : 是信息的最小单位,信息表达的单元。但不是机器指令操作的直接单元。如00110101中,每个0或者1都是一个比特。
位运算也是一种比特量级的运算。
字节(byte): 在绝大多数计算机上都使用8比特作为一个字节,作为最小的内存单位,我们的机器就以字节为单元发出指令,进行寻址。
例如在地址 0xfff19410 这个32位的地址上,每一位f,1,9,4,0都代表了一个字节。我们可以把内存看作一个字节堆叠起来的巨大数组。
| 32位机器内存堆叠模式⬇ | 64位机器内存堆叠模式⬇ |
|---|---|
| 0xffffffff | 0xffffffffffffffff |
| 0xffffffff | 0xffffffffffffffff |
| 0xffffffff | 0xffffffffffffffff |
| 0xffffffff | 0xffffffffffffffff |
| 0xffffffff | 0xffffffffffffffff |
1、左右两排无关,只是简单地表示以下他们在内存上的差异和存储方式,每一个程序都是一个内存块,存放了大量的32/64位字节堆叠起来的数据。
2、注意byte和bit的念法和写法,不要搞混。
1、十六进制
我想大家一定对十六进制不陌生,我在这就不细讲概念了。十六进制是为了压缩存储空间和外部易读性而产生的。它的优越性在于与二进制的无缝衔接,并在数据转换,位运算上也使人能够相对容易理解。
0011 0101 1111 1001
3 5 F 9
注意:在计算机对十六进制的表示上,对于用户的输入端是可以同时接受A~F的大小写的。但程序反馈给用户的一般都是小写,所以我们还是能够尽量规范化表示。
在十六进制的加减乘除上,我们完全可以沿用十进制运算列竖式的操作方式,也就是进位当16,借位也当16的方式。不用再将其转换成其他进制。
2、字数据大小
在386以后,电脑基本上都是32位的CPU,配上了32位的操作系统。但近年来由于互联网时代的高速发展,32位CPU已经不能兼容众多64位的软件了。64位CPU有以下突出的优势:
- 表达数域更为广泛
- 同一时段内处理数据量是32位的两倍。不过要在64位的程序上才能体现出来
- 寻址能力不同,这也决定了内存大小的不同。32位机器上最大能装4GB的内存,而64位的机器上可以存16EB的内存。
1EB = 1024 * 1024 * 1024 GB,是不是超级大。
在不同字长的计算机上,不同的数据类型可能也存在着不同的可容纳空间。这也是对软件的兼容性提出了挑战。
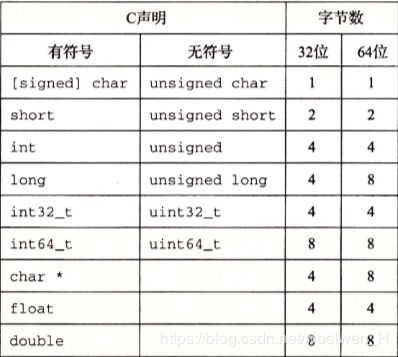
CLRS中明确了字长与部分数据类型之间的一些关系。我们可以看到,long和char* (指针)在不同位下是占不同大小的,所以我们在开发软件的时候一定要注意这一点。
3、寻址和字节顺序
不同机器存储数据的顺序可能不同!我们在这介绍两种数据存储方式:
大端法:最高有效字节在最前面
小端法:最低有效字节在最前面
注意我们在这里只关注有效字节,也就是从高位往低位,出现的第一个非0字节之后的所有内容。
大端法和小端法并没有改变数据本身的顺序,只是修改了程序读取和存储它们的顺序。
在intel兼容机上一般采用小端模式,同样采用小端模式的还有Android 和 ios系统,采用大端模式的就比如有Sun。
举例:
原始数据: f1 94 d1 70
大端存储: f1 94 d1 70
小端存储: 70 d1 94 f1
注意:小端法不是对原始数据的每一个16进制位求翻转,而是把每一个字节作为一个单元求翻转。
4、 布尔代数
布尔代数设计了一种逻辑推理的规则。它包括位运算符和运算法则。
| & ~ ^
上面的运算符运算法则不难懂,难懂的是使用二进制和这几个符号你就可以创造出任意一个东西。
5、位级运算和逻辑运算
1、位级运算就是按位的布尔运算操作,这里的位就是比特位。使用上面已经说明的四个操作符,加上<< >> 等位级运算符就能实现位级运算。任何一个小的操作,在高级语言里看似简单,但如果让我们用位级运算操作并且优化,就显得十分困难,还让代码变得冗长难懂。但它也有它的优越性,位级运算在密码学和网络系统等领域使用的比较广泛,以后学到了再说。
2、逻辑运算就是用 && || ! 等实现命题逻辑里的与或非。这一点理解起来也应该不难。
需要注意的是,在移位操作中,如果我们要求的移位数大于了数据类型本身所具有的位长,机器就会自动执行模数操作。也就是如果一个int类型的数是32位,而你让他右移61位,那么机器就会先用32对61取模得到29,再右移29位。至于实际问题中遇到移位运算优先级的问题,建议直接加括号,不要再讨论优先级。
二、整形表征
1、定义和表征形式
这一部分又叫整数表示,但我认为更好的说法,应该是整形表征。整形是对计算机而言的,它具有范围,而整数是数学里的,不存在范围限制。
整形按照表示内容可以分成两种,补码和无符号,补码是一种有符号的表示方法,有符号数也可以通过原码和反码进行表示。 补码能够表示正负整数和0,无符号数腾出了符号位来表示更多的正整数。而这么一点简单的东西,就足以让人头疼不已。
无符号数是相对简单的。就是普通的二进制转换形式。
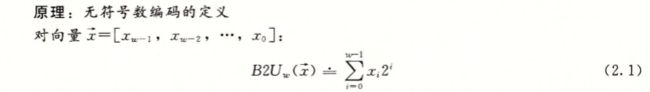
有符号数就没那么简单了。以下是有符号数的编码方式。
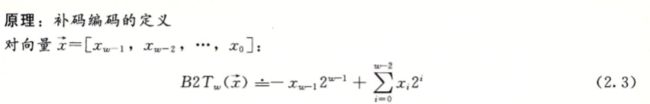

使用原码和反码表示数字时,都会出现+0 和-0同时拥有两种形式的表示方式的情况,为了避免这种情况,我们采用了补码来表示。所以今后我们说一个数的有符号表示,一般都是其补码表示形式。、
在补码表示中,最小数的绝对值比最大数绝对值大1。也就是正负数域不对称的情况。其实这是补码编码定义造成的。原码和反码能够表示出两个0,而补码只有唯一的一个,但相同的位长能够表示相同的数据量,补码少了一个0,便将多出来的这个位置安排给了负数,并将其安排到负数的最后一位。它就是
0x80000000
它是32位补码表示的最小负数。也叫TMin_{32}
2、补码和无符号数之间的转换

有了这三张图片我想我已经不需要多说了吧。补码表示实际上就是把无符号数相对补码正数区域溢出的那一部分拿下来,拼接到0下面,作为负数,就这么简单。
3、关于有符号数和无符号数的一些使用建议
1、在一个运算过程中,如果既有有符号运算数也有无符号运算数,那么有符号运算数会自动转换成无符号运算数。因此不要在一个运算式中同时出现它们。这会造成一些隐式的非语法错误。
2、尽量避免使用无符号数。尤其是在对stl容器遍历的时候。因为只要存在这两者,我们就不得不进行一些特殊操作和特殊考虑,来使得整个程序规范化,而做到这一点又相对麻烦。
3、整型运算
(1)、无符号数操作
1)加法
answer = (x+y) % (2^ω)
2)求反
answer = x == 0 ? 0 : 2^ω-x
3)乘法
answer = (x * y)mod 2^ω
(2)、补码操作
1)求反
answer = x == TMin ? TMin : -x
2)加法
answer = U2T(ω)((x+y) mod2^ω)
3)乘法
answer = U2T(ω)((x * y) mod2^ω)
(3)、除以2的幂
原则:整数除法总是舍入到0,也就是正数向下舍入,负数向上舍入。
在对补码数进行除以2的幂的除法时,负数会向下舍入,为了修正这种不合适的舍入,我们需要加一个偏置。
answer = (x+(1<>k
4、浮点数
浮点数被计算机用来表示有理数。
我们在这里就不讲十进制的表示了,那个谁都知道,不必多说。
我们来看看IEEE-754 std。(这部分我推荐大家还是好好看下书,我在这里只能把稍微关键的地方列一列)
IEEE 754标准给浮点数的设计了如下的存储形式:
- 符号位(s):只占一位,位于整个字段的最高位,记为 f(ω-1)
- 阶码(exp): float 和double的精度不同,阶码的位数也不同。float含有8位阶码而double含有11位。位于f(ω-2)至f(ω-n)位之间。n-2为7或10。阶码是用来表示指数的,但阶码本身不是指数。
- 尾数(frac):是一个二进制小数。存储了被转换成二进制的有效数位。

这张图可以帮助理解各个数码部分存储的相对位置。
然后我们介绍两个概念:规格化数和非规格化数。为了方便,我们这里讨论单精度数值,双精度和单精度的解释一样,就换个精度。
规格化数:阶码数值从 [ 1 ] 到 [ 2 ^ {8} -2 ] 不等。设阶码为m, 实际指数 e = m - ( 2 ^ {8-1} -1 )。 我们可以由此得到规格化数的指数范围为 [ 2 - 2 ^ {7}, 2 ^ {7} - 1 ]之间的每一个整数。而尾数部分的取值范围是 [0, 2 ^ 23]。
非规格化数:阶码数值只能为0, 设阶码为m, 实际指数 e = 2 - 2 ^ { 8 - 1 }。尾数部分的取值范围为 [1, 2 ^ 23]。
原理:这样的表示方法,是将一个任意进制的数值,先转化成二进制(这个二进制的首位必然是1),再取首位后面的所有位作为尾数部分,将尾数的个数作为指数的大小,再将指数转换成阶码,加上符号位,这样就表示成了一个符合IEEE 754 的浮点数。这个表示方法里,由于原二进制码的第一位必然是1,所以我们直接将这一位省略,腾出一个位置。但是我们反向推导原数的时候一定要考虑到这一点。
我们直接举几个特殊的例子来算:
最大的正非规格化数值: 0 0000 0000 111 1111 1111 1111 1111 1111
answer = 2 ^ {2-2^{7}} * (1-2^{-23})
最小的非规格化数值: 0 0000 0000 000 0000 0000 0000 0000 0001
answer = 2 ^ {2-2^{7}} * 2^{-23}
最大的规格化数: 0 1111 1110 111 1111 1111 1111 1111 1111
answer = 2 ^ {2^{7}-1} * (2^24-1) * (2^{-23})
最小的正规格化数:0 0000 0001 000 0000 0000 0000 0000 0000
answer = 2 ^ {2-2^{7}}
零的表示:全0
正无穷的表示:0 1111 1111 000 0000 0000 0000 0000 0000
规格化数和非规格化数的衔接是非常顺滑的,它们的边界十分接近。我们从上面的计算可以看到最大的非规格化数值和最小的规格化数值只差了
2^{2-2^{7]}*2^{-23}
这个数是非常非常小的。
在浮点数运算中,我们必须考虑误差。因为浮点数表示的是有穷二进制数。对于相当一部分无穷二进制数,是不能够精确表示的。有时虽然我们的精度很细,但经过时间的积累,有可能是一个相当大的误差,这不得不引起我们的重视。