O(N)最长回文子串算法——Manacher算法

题目举例：http://hihocoder.com/problemset/problem/1032?sid=763559

题意：在一串连续的字符串中寻找它的最长子串（Longest Palindromic Substring）

输入：先从标准输入读取一个整数N（N<=30)，代表字符串的个数，接下来N行给出N个字符串（字符串长度<=10^6)

输出：最长回文子串长度

 

       题目分析：很自然地想到这样的算法，长度为n的字符串，它的最大回文子串长度为n，那么按长度递减的顺序去原串中查找，依次寻找是否有长度为n、n-1、n-2……的子串，一旦找到就跳出循环；回文串的判断则用一个函数实现，从两端往中间比较。方法是对的，不过这个算法的时间复杂度是O(N^3)，题目的字符串可能很长（10^6），肯定会超时。

       上面的求解思路，我们容易发现，它实际上会进行很多重复的比较。假设字符串为：ACABA，在判断长度为5的子串是否有回文串的时候，比较了C和B，在判断长度为3的子串时，再次比较了C和B。当字符串很长的时候，这种重复的比较将普遍存在，如果长度为n的字符串中每个字符都不相同（即最长回文子串的长度为1），则长度为k的回文串判断，进行的比较次数为⌊k/2⌋，n中一共包含n-k+1个长度为k的子串，则进行 (n-k+1)*⌊k/2⌋次比较，所以从n~ 2一共进行的比较次数为：

       如何减少重复比较是提升算法效率的关键。实际上，解决该问题有个很经典的算法：Manacher算法，下面来看它是如何减少重复比较次数的。

       Manacher算法判断回文串的方法和上述略微不同，它是从中心字符出发，向两端移动比较，但是这样只能解决长度为奇数的字符串判断，因为对于偶数长度，实际上并不存在所谓的中心字符。这里有个巧妙的方法，将所有字符串都转化成奇数长度：在原串的每两个字符之间都填上一个特殊字符（它不能存在于原串中，一般用‘#’作为特殊字符），同样在头和尾也补充该字符，所以字符串长度变成2*N+1，字符串的形式为：#C#C#C#C#（C表示原串的字符）。

       Manacher算法从头开始对每个字符计算以它为中心的最长回文串长度，遍历一次得到最长回文串长度。当然如果老老实实对每个字符都从±1的位置开始比较，那么算法时间复杂度是O(N^2)，Manacher算法当然不是这么做的。

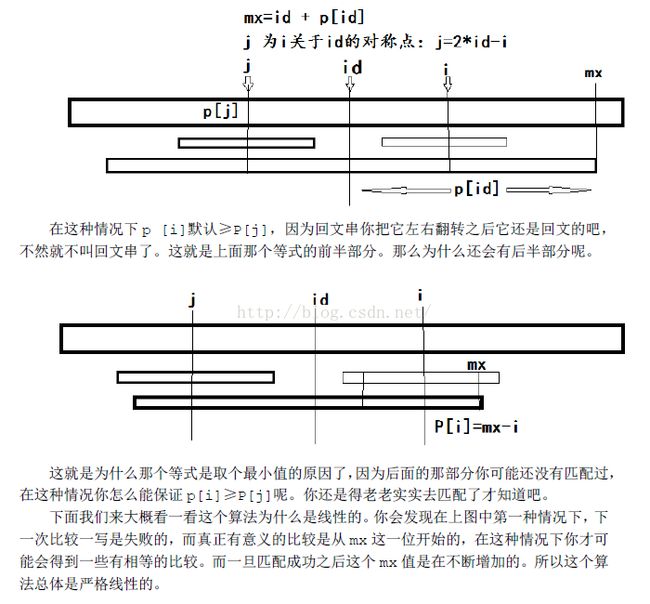
       定理1. 假设有回文串S，其中心下标为md，则有S[md+i] = S[md-i], i≤S.length()/2.

       推论1. 假设有回文串S，其中心下标为md，i,j (i < j)是关于md对称的两个下标，则由定理1有S[i+k]= S[j-k], S[i-k] = S[j+k], 其中i,j和k的加减法不超过S的范围。

       推论2. 若用lps[]存放S中每个字符为中心的最长回文串长度，由推论1，在S的范围内，有lps[j]= lps[i]，因为i = md-(j-md)，也可以写作lps[j] = lps[2*md - j].

       推论3. 假设有回文串S，其中心下标为md，i,j (i < j)是关于md对称的两个下标，则由推论2，有lps[j]= min{ lps[i], mx - j }或lps[j]= min{lps[2*md - j], mx - j}，其中mx为S的右端。

       下图解释了推论3中的min操作，假如lps[i]没有超过S的边界，那么lps[j] = lps[i];假如lps[i]超过或恰好到达S的边界，那么超过的部分，lps[i]无法成为lps[j]的保证，从越过边界(mx)的位置开始，lps[j]必须往两端一一比较，lps[j]=mx - j（这里有个等价关系，lps[]既表示去掉#以后最长回文串长度，也表示#存在时单边的长度）。推论3中的这条语句，是Manacher算法的核心，理解了它也就理解了Manacher算法。

下面给出完整的代码：

#include 
using namespace std;

char str[2000005];
int  lps[2000005];
int Manacher(string s)//manacher algorithm
{
	int length = s.size(), j = 2;
	str[0] = '$'; str[1] = '#';
	//插入#
	for(int i = 0; i < length; i++)//$#c#c#c#'\0'
	{
		str[j++] = s[i];
		str[j++] = '#';
	}
	str[j] = '\0';
	length = (length << 1) + 2;
	
	lps[0] = 1;
	int mx = 0, md = 0, max_len = 0;//当前回文串能达到的最右端，及其中心
	for(int i = 1; i= mx)  lps[i] = 1;
		else  lps[i] = min(lps[2*md-i], mx-i);
		while(str[i-lps[i]] == str[i+lps[i]])
			lps[i]++;

		if(i+lps[i] > mx)
		{
			mx = i+lps[i];
			md = i;
		}
		if(lps[i] > max_len)  
			max_len = lps[i];
	}
	printf("%d\n", max_len-1);
}
int main()
{
	int n;  
	string s;
	cin >> n;
	while(n--)
	{
		cin >> s;
		Manacher(s);
	}
	return 0;
}

       上述代码的实现和之前讨论略有不同，一个处理细节是在开头加上了'$'，这是因为字符串结尾为'\0'，所以需要在头部加一个字符维持奇数长度；另外，如果加'#'，那么在字符串#a#b#a#c#d#a#计算第一个a的lps值时，会越过0的数组边界。所以在开头加'$'充当“哨兵”，这样就免去了在while循环中判断越界，另外在字符串的末尾，有'\0'保证不会越界，如果同时到达了字符串的开头和末尾，因为'#'!='$'，所以也不会越界。

 

参考文章：http://www.cnblogs.com/easonliu/p/4454213.html