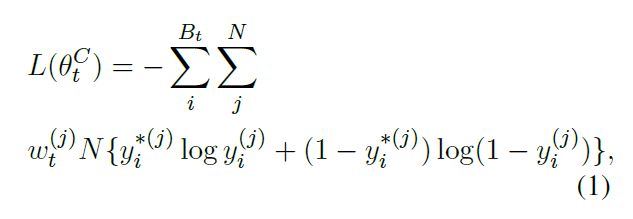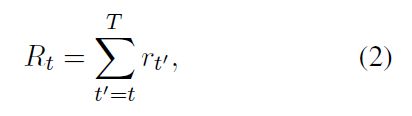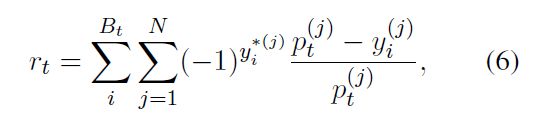Learning to Learn and Predict: A Meta-Learning Approach for Multi-Label Classification
2019-10-01 11:29:54
Paper: https://arxiv.org/pdf/1909.04176.pdf
1. Background and Motivation:
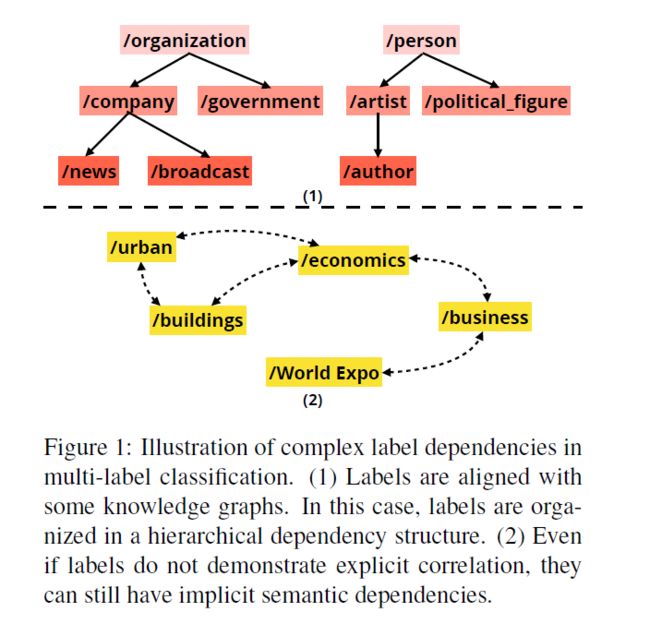
多标签分类问题的目标是同时进行多个 label 的识别,且这些 label 是有一定关联的;而传统的 多类别分类问题,仅仅是一个样本包含一个 label。现有的方法,从统计模型到神经网络的方法,都是共享标准的交叉熵损失函数进行训练的。在训练之后,这些模型尝试用单个预测策略来对所有的 label 进行最终的预测。实际上,这些方法都是基于如下的假设:no dependency among the labels。然而,如图1 所示,这种假设在实际情况下是很难满足的,但是 multi-label classification 的 label 依赖关系的问题却很少受到关注。
由于受到标签依赖关系的影响,这些 label 的预测难度是大不相同的。
首先,高层的 label 更加容易进行分类,如:organization,person 等;但是更加低层的 label,如 news,broadcast 等,则更加困难。
其次,对于 label 之间没有显示关系的,可能仍然存在着一些隐层的关系,这在 NLP 领域中,是相当常见的。
基于上述观察,作者考虑学习不同的训练策略 和 预测策略来进行多标签的识别。
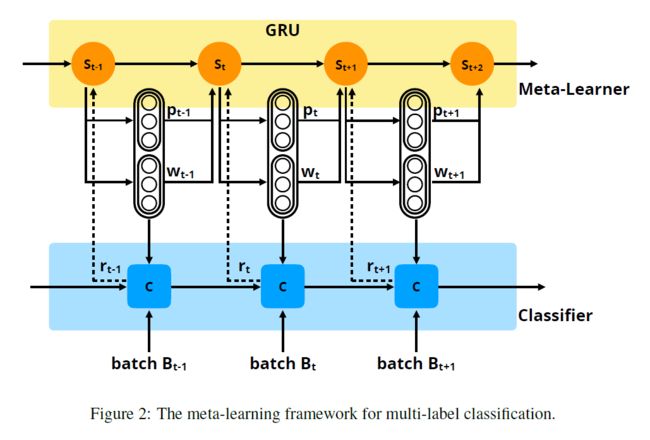
对于所有 label 的训练和预测策略,可以看做是一系列的超参数。然而,想要指定显示和隐式的标签依赖,也是不显示的。为了解决上述问题,本文提出一种 meta-learning 的框架来建模这些 label dependency,然后自动的学习训练和测试策略。具体来说,作者引入一种联合 meta-learning 和 multi-label classification 的学习框架。作者用一种基于 GRU 的 meta-learner 在训练阶段来捕获 label dependencies 和 学习这些参数。
本文的贡献可以总结为如下几点:
1). 首次在多标签分类问题上,提出联合的 “learning to learn” 和 “learning to predict” 。
2). 本文方法可以对每一个 label 学习一个 weight 和 decision policy,并且可以用于训练和测试阶段。
3). 本文方法是一种 model-agnostic,可以结合到多种模型中,并且取得了比 baseline 方法要好很多的效果。
2. The Proposed Method:
2.1 Classifier Model:
对于一个 N 类的多标签分类问题来说,我们将训练策略表示为 w,测试策略表示为 p,其中 wi 和 pi 是第 i 类的训练权重和预测阈值。wt 和 pt 表示时刻 t 的权重向量和阈值向量。然后,本文的学习目标就变成了:learn a high-quality w and p for a certain classifier C. 为了更新分类器 C 的参数,作者在每个时刻采样一个 batch Bt。然后设置一个加权的交叉熵目标函数来更新 C,定义如下:
其中,$y_i^*$ 表示 第 i 个样本的真值,$y_i^{(j)}$ 是输出向量 yi 的第 j 个 值。
2.2 Meta-Learner:
作者这里认为 meta-learning 是一种 reinforcement learning 技术。而每一个时刻,meta-learner 观测到当前的状态 st,然后产生一个训练策略 wt 和 测试策略 pt,基于这些策略,分类器 C 的参数可以进行更新。在训练后,meta-learner 接收到一个奖励 rt。而本文 meta-learner 的目标就是选择两个策略,使得将来的奖励最大化:
2.2.1 State Representation:
在本文中,作者将 meta-learner 建模为 RNN 结构,实际上用的是 GRU。状态表达 st 直接定义为 GRU 在每一个时刻 t 的隐层状态 ht。然后,st 是根据如下的公式进行计算的:
其中,GRU 在 时刻 t 的输入是预测策略和训练策略的组合。
2.2.2 Policy Generation:
在每一个时间步骤,meta-learner 可以产生两个策略,即:训练策略 wt 和 预测策略 pt。这两个策略均被表达为 N-dimensional 的向量格式。为了将训练策略 wt 结合到交叉熵的目标函数中,并且保持 classifier 的训练梯度在同一个数量级,wt 需要满足加和为 1 的约束。然后,在每一个时刻 t,训练策略可以按照如下的方法得到:
对于测试策略,其定义为:
在上述两个公式中,除了 st 是状态外,其他的参数都是可学习的参数。
2.2.3 Reward Function:
奖励按照如下的公式进行计算:
其中,$y_i$ 是第 i 个样本的输出概率,$y_i^*$ 是对应的真值向量。作者这里也给了一个例子,来说明奖励的计算过程:
2.3 Training and Testing: