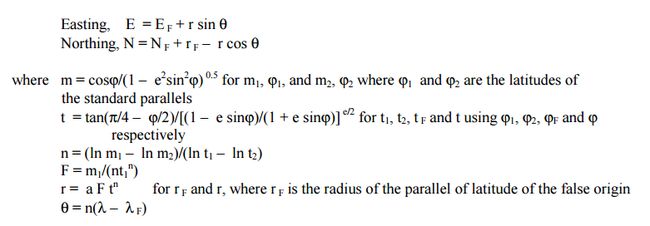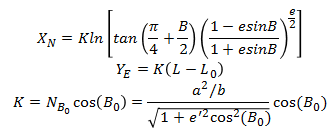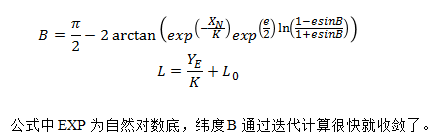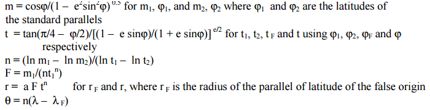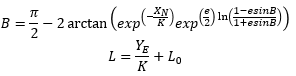hello~~今天yogurt要和大家分享的是如何玩转地图投影的公式,由正解公式求解:(Lat,Lon)-->(E,N),或者由反解公式求解:(E,N)-->(Lat,Lon)。关于怎么进行投影?大家可以参考我之前写过的一篇《.gen地图文件的投影编程实现(以墨卡托投影和兰伯特投影为例)》http://www.cnblogs.com/to-sunshine/p/6048438.html。接下来,yogurt先给大家简单介绍一下地球椭球及其参数,还有兰伯特投影和墨卡托投影公式,让大家对于投影这个概念和过程有个大致地了解。然后,通过两个例子分别对兰伯特投影和墨卡托投影进行正反算求解。
============================yogurt小课堂开课了===========================
什么叫做地球椭球?我们都知道地球是一个两边宽上下扁的不规则椭球体。那么为了简化计算,我们把这个椭球体近似看作一个标准椭球体,它拥有以下参数:
长半径:a ; 短半径:b ;
扁率与偏心率的关系为:e ² = 2 X f - f ² 。
当然,地球椭球体与普通标准椭球体还是有一定区别的,下面的参数则是地球椭球体特有的: 首先,我们要来了解这两个概念:
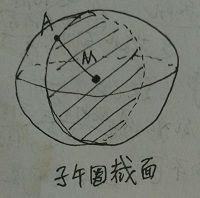
法截面:设过椭球表面上任意一点A做法线AL,通过法线的平面所截成的截面;
子午圈截面:包含子午圈的椭球体截面; --> 对应曲率半径  (该半径对应的圆弧是与所有经线相平行的)
(该半径对应的圆弧是与所有经线相平行的)
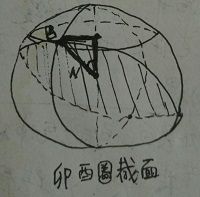
卯酉圈截面:垂直于子午圈截面的法截面。 --> 对应曲率半径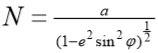 (该半径cos之后得到的半径是对应的纬线圈上的半径,对应的圆弧是与所有纬线相平行的)
(该半径cos之后得到的半径是对应的纬线圈上的半径,对应的圆弧是与所有纬线相平行的)
如图:
假设某点 纬度:ρ 经度:λ
由 弧长 l = 半径 r X 弧度φ 得到:
南北方向弧长:dN = M X dρ , 东西方向弧长:dE = (N X cosρ) X dλ 。
------------------------------------------------------------------------------------------------------------------------------------------------
什么叫做地图投影呢?即:建立平面上的点(用平面直角坐标或极坐标表示) 和地球表面上的点(用纬度Φ和经度λ表示)之间 的函数关系,用数学表达这种关系,就是:
兰伯特投影:是等角正轴割圆锥投影; 墨卡托投影:是等角正切圆柱投影。
------------------------------------------------------------------------------------------------------------------------------------------------
1、 利用兰伯特等角投影正解和反解公式进行求解
正解公式由(Lat,Lon)à(E,N):
注:设原点纬度为,原点经度为,第一标准纬线φ1,第二标准纬线φ2,则:
反解公式由(E,N)à(Lat,Lon):
注:设原点纬度为,原点经度为,第一标准纬线φ1,第二标准纬线φ2,则:
2、 利用墨卡托投影的正解和反解公式进行求解
正解公式由(B,L)à(X,Y):
注:设标准纬度B0,原点纬度0,原点经度L0
反解公式由(X,Y)à(B,L):
注:设标准纬度B0,原点纬度0,原点经度L0
=================================下课了================================
下面用两道例题来实践一下这个正反解算过程。
第一题:根据Clarke 1986椭球体及以下参数,利用兰伯特投影求解 Lat = 28°30’ N ,Lon = 96° W的N、E坐标,然后反算Lat/Lon,写出主要步骤。已知该椭球体的参数如下:
a = 6378206.400 m 1/f=294.97870
原点纬度: 27°50’N 原点经度: 99° W
第一标准纬线纬度: 28°23’ N 第二标准纬线纬度:30°17’ N
东偏移: 609,600 meter 北偏移: 0 meter
------------------------------------------------------------------------------------------------------------------------------------------------
一、正解![]() :
:
1、参数分析:
可知,需要求出未知参数r、rf和角度,这三个参数也有求解公式。
观察参数的求解公式:
可知,m公式可以算出m1和m2,;t公式可以算出t1和t2和tf;n和f的值是唯一的;还需要根据扁率f算出椭圆的第一偏心率e。
2、求解过程:
(1)首先根据f的值求出基本参数e;
(2)然后就可以根据e的值和已知点的纬度以及第一和第二标准纬线算出m1、m2和t、t1、t2、tf的值;
(3)接着就可以根据m1、m2和t1、t2算出n的值;
(4)再根据m1、t1和n可以算出未知参数角度和F;
(5)最后根据这些参数可以算出最后的未知参数 r 和 rf 的值。
(6)将求解出来的r和角度带入公式![]() ,得到投影后的经度;
,得到投影后的经度;
将求解出来的rf和角度带入公式![]() ,得到投影后的纬度。
,得到投影后的纬度。
3、结果:(903253.1578,169962.9044),过程超级难算的,这个结果yogurt也不敢保证正确哦(〒_〒)
二、反解![]() :
:
1、参数分析:
可知,需要求出未知参数t’、e以及 θ‘ 和n,尤其第一个公式未知数 φ 同时在等式的两侧就需要迭代直到两次迭代的结果非常接近为止,另外的四个参数也有求解公式。
观察参数的求解公式:
可知,Ef、Nf是题目中已知的假东和假北值,e、n、F、rf可以用正解中算出的值对应,剩下的r’、t’、角度’是需要求的。
2、求解过程:
(1)根据E、Ef和rf、N、Nf求出r’和角度’;
(2)根据r’的值和a、F、n求出t’;
(3)最后把t’和e带入到公式,假设 φ 的值为25°N带入公式右边,![]()
计算之后得到一个新的 φ1,将 φ1带入公式右边,计算得到 φ2,重复带入公式右边,直到某个 φ 带入后算出来的 φ 值和带入前非常接近为止,得到 φ 最终的结果;
把角度 θ’、和n还有原点经度带入公式![]() ,得到投影前的经度值。
,得到投影前的经度值。
3、结果:(96,28.5)过程超级难算的,这个结果yogurt也不敢保证正确哦(〒_〒)
========================================================================
第二题:根据Krassowski 1940椭球体及以下参数,利用墨卡托投影求解 Lat = 53°00’ N ,Lon = 53° E的N、E坐标,然后反算Lat/Lon,写出主要步骤。已知该椭球体的参数如下:
a = 6378245.0 m 1/f = 298.3
原点经度:51° W 第一标准纬线纬度:42° N
西偏移:300,000 meter 北偏移:300,000 meter
------------------------------------------------------------------------------------------------------------------------------------------------
一、正解![]() :
:
1、参数分析:
可知,需要求出未知参数e和K,K也有求解公式。
观察参数的求解公式:
可知,除了题目已知参数外,还需要算出椭球体的短半轴和第二偏心率e’。
2、求解过程:
(1)根据扁率 f 和第一偏心率的关系算出第一偏心率e;
(2)根据 e 和 a 的关系可以算出短半轴 b 的值;
(3)根据 a 和 b 可以算出第二偏心率 e’;
(4)根据 K 的求解公式,利用a、b和 e’ 以及标准纬度 B0 的值算出K;
(5)将K和e代入公式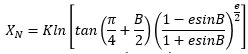 ,得到投影后的纬度;将K代入公式
,得到投影后的纬度;将K代入公式![]() ,得到投影后的经度值。
,得到投影后的经度值。
3、结果:(-162372.5867,5067861.1471)同样,过程超级难算的,这个结果yogurt也不敢保证正确哦(〒_〒)
二、反解![]() :
:
1、参数分析:
可知其他所需的参数分别是K和e可以用正解中算出值,以及题目中已知的原点纬度L0。
2、求解过程:
(1)根据Y、K和原点经度L0,利用公式![]() 直接得到投影前的经度;
直接得到投影前的经度;
根据EXP、K、X和e的值带入公式,假设B的值为50°N带入公式右边,![]() ,得到一个新的B1,再将B1带入公式右边得到B2,重复带入,直到带入前和带入后的值非常接近时为止,得到投影前的纬度值。
,得到一个新的B1,再将B1带入公式右边得到B2,重复带入,直到带入前和带入后的值非常接近时为止,得到投影前的纬度值。
3、结果:(53,53)同样,过程超级难算的,这个结果yogurt也不敢保证正确哦(〒_〒)~~
好啦,今天yogurt就和大家讲到这里啦,大家有什么不明白的可以评论提问,我看到就会解答哒~~