细胞自动机

细胞自动机是指定形状的网格上的“有色”单元的集合，其根据基于相邻单元的状态的一组规则通过多个离散时间步长演变。然后根据需要迭代地应用规则多个时间步长。冯·诺伊曼是最早考虑这种模型的人之一，并将细胞模型纳入他的“通用构造函数”。20世纪50年代早期，细胞自动机被研究作为生物系统的可能模型。自20世纪80年代开始，S. Wolfram对细胞自动机进行了全面的研究，Wolfram在该领域的基础研究最终发表了他的着作“新的科学 ” 一书。 （Wolfram 2002）其中Wolfram提出了一系列关于自动机的巨大结果，其中包括许多突破性的新发现。

电视犯罪剧“ NUMB3RS ”的第2季“ Bettor or Worse ”（2006） 提到了一维细胞自动机。

细胞自动机有各种形状和种类。元胞自动机的最基本属性之一是计算它的网格类型。最简单的这种“网格”是一维线。在二维中，可以考虑方形，三角形和六边形网格。细胞自动机也可以在任意数量的维度上构建在笛卡尔网格上，其中 - 维整数格是最常见的选择。一维整数格上的元胞自动机在Wolfram语言中实现为CellularAutomaton [ rule， init，步骤 ]。

还必须指定元胞自动机可以假设 的颜色（或不同状态）的数量。这个数字通常是一个整数，（二进制）是最简单的选择。对于二元自动机，颜色0通常称为“白色”，颜色1通常称为“黑色”。然而，也可以考虑具有连续范围的可能值的细胞自动机。

除了细胞自动机所在的网格和细胞可能呈现的颜色之外，还必须指定细胞彼此影响的邻域。最简单的选择是“最近邻居”，其中在每个时间步骤中只有与给定单元直接相邻的单元可能受到影响。在正方形网格上的二维元胞自动机的情况下的两个常见邻域是所谓的摩尔邻域（正方形邻域）和冯诺依曼邻域（菱形邻域）。

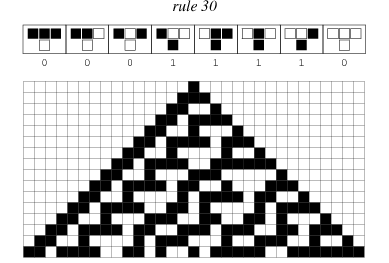
最简单类型的元胞自动机是二元，最近邻，一维自动机。这种自动机被S. Wolfram 称为“ 基本细胞自动机 ”，他已经广泛研究了它们的惊人特性（Wolfram 1983; 2002，第57页  ）。有256个这样的自动机，每个自动机都可以用唯一的二进制数索引，其十进制表示被称为特定自动机的“规则”。上面示出了规则30的图示以及从单个黑色单元开始的15个步骤之后产生的演变。

一类稍微复杂的细胞自动机是最近邻，彩色，一维全局细胞自动机。在这样的自动机中，相邻单元的平均值决定了演化，最简单的非平凡例子有颜色。对于这些自动机，该组的描述行为规则可以被编码为位数字称为一个进制数“代码”。以上说明了三元（）代码912自动机的规则和300步骤。

在两个方面，最着名的元胞自动机是康威的生命游戏，由J. H. Conway于1970年发现并在Martin Gardner的Scientific American专栏中得到推广。在生活的游戏是一个二进制（）极权元胞自动机与摩尔附近 的范围。尽管生命世代的连续游戏的计算 最初是手工完成的，但计算机革命很快就到来了，并且允许更广泛的模式被研究和传播。以上示出了被称为河豚列车的生命建筑游戏的动画。

WireWorld是另一种常见的二维元胞自动机。

细胞自动机理论非常丰富，简单的规则和结构能够产生各种各样的意外行为。例如，存在 能够模拟任何其他元胞自动机或图灵机的行为的通用细胞自动机。Gacs（2001）甚至已经证明存在容错的通用细胞自动机，其模拟其他细胞自动机的能力不受随机扰动的阻碍，条件是这种扰动足够稀疏。

转载于:https://my.oschina.net/lanhaikeji/blog/3084468