LeetCode Weekly Contest 197

1512. 好数对的数目

给你一个整数数组 nums 。

如果一组数字 (i,j) 满足 nums[i] == nums[j] 且 i < j ，就可以认为这是一组 好数对 。

返回好数对的数目。

示例 1：

输入：nums = [1,2,3,1,1,3]
输出：4
解释：有 4 组好数对，分别是 (0,3), (0,4), (3,4), (2,5) ，下标从 0 开始
示例 2：

输入：nums = [1,1,1,1]
输出：6
解释：数组中的每组数字都是好数对
示例 3：

输入：nums = [1,2,3]
输出：0

提示：

1 <= nums.length <= 100
1 <= nums[i] <= 100

思路

哈希表统计每个数字出现的次数，根据出现次数运用组合数公式计算

代码

class Solution {
    private int factor(int n) {
        return n * (n - 1) / 2;
    }
    
    public int numIdenticalPairs(int[] nums) {
        HashMap<Integer, Integer> cnts = new HashMap<>();
        for (int num: nums) {
            if (!cnts.containsKey(num)) {
                cnts.put(num, 0);
            }
            cnts.put(num, cnts.get(num) + 1);
        }
        int ans = 0;
        for (int cnt: cnts.values()) {
            if (cnt > 1) {
                ans += factor(cnt);
            }
        }
        return ans;
    }
}

1513. 仅含 1 的子串数

给你一个二进制字符串 s（仅由 ‘0’ 和 ‘1’ 组成的字符串）。

返回所有字符都为 1 的子字符串的数目。

由于答案可能很大，请你将它对 10^9 + 7 取模后返回。

示例 1：

输入：s = “0110111”
输出：9
解释：共有 9 个子字符串仅由 ‘1’ 组成
“1” -> 5 次
“11” -> 3 次
“111” -> 1 次
示例 2：

输入：s = “101”
输出：2
解释：子字符串 “1” 在 s 中共出现 2 次
示例 3：

输入：s = “111111”
输出：21
解释：每个子字符串都仅由 ‘1’ 组成
示例 4：

输入：s = “000”
输出：0

提示：

s[i] == ‘0’ 或 s[i] == ‘1’
1 <= s.length <= 10^5

思路

统计每段连续1字符的个数，运用组合数公式计算

代码

class Solution {
    private static final long mod = 1000000007;
    
    /**
    * n * (n + 1) / 2
    */
    private long factor(int n) {     
        long nl = (long)n;
        return (nl * (nl + 1) / 2) % mod;
    }
    
    public int numSub(String s) {
        int cnt = 0;
        long ans = 0;
        for (char ch: s.toCharArray()) {
            if (ch == '1') {
                ++cnt;
            } else {
                ans = (ans + factor(cnt)) % mod;
                cnt = 0;
            }
        }
        ans = (ans + factor(cnt)) % mod;
        return (int)ans;
    }
}

1514. 概率最大的路径

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例 1：

输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25
示例 2：

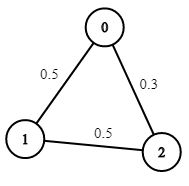
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
输出：0.30000
示例 3：

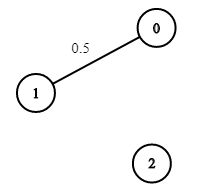
输入：n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
输出：0.00000
解释：节点 0 和 节点 2 之间不存在路径

提示：

2 <= n <= 10^4
0 <= start, end < n
start != end
0 <= a, b < n
a != b
0 <= succProb.length == edges.length <= 2*10^4
0 <= succProb[i] <= 1
每两个节点之间最多有一条边

思路

满足局部性：概率最大的路径的子路径也是概率最大，使用优先队列优化的Dijkstra算法

代码

class Solution {
    class Node implements Comparable<Node> {
        public int id;
        public double prob;
        
        public Node(int _id, double _prob) {
            id = _id;
            prob = _prob;
        }
        
        @Override
        public int compareTo(Node other) {
            if (other.prob > prob) {
                return 1;
            } else {
                return -1;
            }
        }
    }
    
    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
        double[] dis = new double[n];
        boolean[] vis = new boolean[n];
        PriorityQueue<Node> pq = new PriorityQueue<>();
        HashMap<Integer, ArrayList<Integer>> adj = new HashMap<>();
        HashMap<Integer, HashMap<Integer, Double>> weights = new HashMap<>();
        dis[start] = 1.0;
        pq.add(new Node(start, 1.0));
        int ecnt = 0;
        for (int[] edge: edges) {
            if (!adj.containsKey(edge[0])) {
                adj.put(edge[0], new ArrayList<Integer>());
            }
            if (!adj.containsKey(edge[1])) {
                adj.put(edge[1], new ArrayList<Integer>());
            }
            if (!weights.containsKey(edge[0])) {
                weights.put(edge[0], new HashMap<Integer, Double>());
            }
            if (!weights.containsKey(edge[1])) {
                weights.put(edge[1], new HashMap<Integer, Double>());
            }
            adj.get(edge[0]).add(edge[1]);
            adj.get(edge[1]).add(edge[0]);
            weights.get(edge[0]).put(edge[1], succProb[ecnt]);
            weights.get(edge[1]).put(edge[0], succProb[ecnt]);
            ++ecnt;
        }
        while (!pq.isEmpty()) {
            Node head = pq.poll();
            if (head.id == end) {
                break;
            }
            if (!vis[head.id]) {
                vis[head.id] = true;
                dis[head.id] = head.prob;
                // System.out.println(head.id + " " + head.prob);
                if (adj.containsKey(head.id)) {
                    for (int id: adj.get(head.id)) {
                        if (!vis[id] && head.prob * weights.get(head.id).get(id) > dis[id]) {
                            dis[id] = head.prob * weights.get(head.id).get(id);
                            pq.add(new Node(id, dis[id]));
                        }
                    }
                }
            }
        }
        return dis[end];
    }
}

5463. 服务中心的最佳位置

一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标，并希望能够以此为依据为新的服务中心选址：使服务中心 到所有客户的欧几里得距离的总和最小 。

给你一个数组 positions ，其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置，返回到所有客户的 欧几里得距离的最小总和 。

换句话说，请你为服务中心选址，该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值：

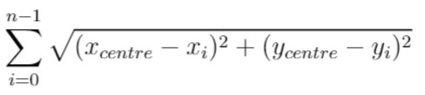
与真实值误差在 10^-5 之内的答案将被视作正确答案。

示例 1：

输入：positions = [[0,1],[1,0],[1,2],[2,1]]
输出：4.00000
解释：如图所示，你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置，这样一来到每个客户的距离就都是 1，所有距离之和为 4 ，这也是可以找到的最小值。
示例 2：

输入：positions = [[1,1],[3,3]]
输出：2.82843
解释：欧几里得距离可能的最小总和为 sqrt(2) + sqrt(2) = 2.82843
示例 3：

输入：positions = [[1,1]]
输出：0.00000
示例 4：

输入：positions = [[1,1],[0,0],[2,0]]
输出：2.73205
解释：乍一看，你可能会将中心定在 [1, 0] 并期待能够得到最小总和，但是如果选址在 [1, 0] 距离总和为 3
如果将位置选在 [1.0, 0.5773502711] ，距离总和将会变为 2.73205
当心精度问题！
示例 5：

输入：positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
输出：32.94036
解释：你可以用 [4.3460852395, 4.9813795505] 作为新中心的位置

提示：

1 <= positions.length <= 50
positions[i].length == 2
0 <= positions[i][0], positions[i][1] <= 100

思路

此题属于数值优化算法。
牛顿法求最小值，为了避免震荡不收敛，在经典牛顿法的更新公式中加入一个小于1的学习率，对学习率进行调参（此处学习率为0.6是反复调参结果，只是恰好通过了LeetCode上的所有测试数据，不能保证对于所有数据均能收敛）
理论上牛顿法是二阶收敛的，在初值合适的情况下，收敛速度比梯度下降快

代码

class Solution:
    NON_ZERO = 1e-12
    
    def dist(self, pos0, pos1):
        return math.sqrt((pos0[0] - pos1[0])**2 + (pos0[1] - pos1[1])**2)
    
    def grad(self, center, positions, axis):
        return sum([(center[axis] - pos[axis]) / (self.dist(center, pos) + Solution.NON_ZERO) for pos in positions])
    
    def grad2(self, center, positions, axis):
        return sum([(1/(self.dist(center, pos) + Solution.NON_ZERO) - (center[axis] - pos[axis])**2/(self.dist(center, pos)**3 + Solution.NON_ZERO)) for pos in positions])
    
    def getMinDistSum(self, positions: List[List[int]]) -> float:
        n = len(positions)
        if n == 1:
            return 0.0
        lr = .6
        center = [sum([pos[axis] for pos in positions])/n for axis in range(2)]
        while True:
            preCenter = center.copy()
            center = [center[axis] - lr * self.grad(center, positions, axis) / (self.grad2(center, positions, axis) + Solution.NON_ZERO) for axis in range(2)]
            if self.dist(center, preCenter) < 1e-10:
                break
        return sum([self.dist(center, pos) for pos in positions])