网络原理考点之链路状态路由算法计算部分
链路状态路由算法,给出的例子便是迪科斯彻算法,Dijkstra,尽管在2018年8月23日用C和C++实现了算法,详见《迪科斯特算法》,但好像没有用文字总结一下,结合题再加深下吧。
如题:2018年10月
分析:
要解决的问题:
广度优先搜索解决赋权有向图或者无向图的单源最短路径问题。
思路:
Dijkstra算法采用的是一种贪心的策略,声明一个数组dis来保存源点到各个顶点的最短距离
另一个保存已经找到了最短路径的顶点的集合T。
步骤:
1、从dis数组选择最小值,则该值就是源点s到该值对应的顶点的最短路径,并且把该点加入到T中。
2、重新计算新加入的顶点到达其他点的路径长度是否比源点直接到达短,如果是,那么就替换这些顶点在dis中的值。
3、从dis中找出最小值,重复1~3.直到遍历完树(此时的树是脑补出来的),最终的dis数组就是最短的距离。
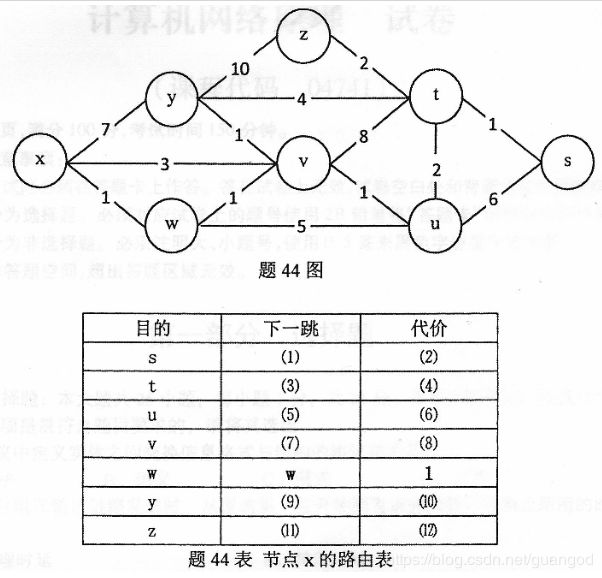
下面结合题来做一下详细的分析:
树已经给画出来了,所以不需要脑补了。下面就是求迪科斯彻算法就行了。
根据以上的步骤:
1、选建立一个从源点开始的最短路径数组及最短路径顶点数组:T[]={x},dis[]={dis[x]=0,dis[y]=7,dis[v]=3,dis[w]=1};
注:dis[*]代表从选定的最短顶到到*的距离,如dis[y],代表从x到y的距离
2、从dis中找到距离最小的路径显然是dis[w],将W加入到T中,然后重新从W出发计算与它直连边的距离。T[]={x,w};dis[]={dis[v]=1+dis[w]=1+1=2,dis[u]=5+dis[w]=6}+{dis[y]=7,dis[v]=3}(之前)dis[v]要小于之前的2<3,所以更新下dis[v]=2.现在dis[]={dis[v]=2,dis[u]=6,dis[y]=7};从这里面找最短的,那就是dis[v],
3、将v点加入到T[]={x,w,v},重新计算从v结点出发计算与它直边边距离,已经在集合T中的点不看。dis[]={dis[y]=1+dis[v]=3小于之前的值7,所以更新下dis[y]=3,dis[t]=8+dis[v]=10,dis[u]=1+dis[v]=3};现在的dis[]={dis[y]=3,dis[t]=10,dis[u]=3}+{dis[u]=6}发现dis[u]也有了更小值,所以需要更新dis[]={dis[y]=3,dis[t]=10,dis[u]=3}
这个更新的思想,便是dijkstra算法的核心了,这个过程叫”松弛“,通过中间边来松弛源点到中间各个顶点的距离。
4、剩下的便是重复以上步骤直到各个顶点加入到T中来。
现在有dis[y]==dis[u],两个最短边距,取哪个顶点加入T呢?题目告诉了,要选择编号小的节点加入,u在y前,所以选择u加入T.
T[]={xwv,u};wv在T,不需要看,只看ts,所以dis[]={dis[t]=2+dis[u]=5,dis[s]=6+dis[u]=9}对比上一步dis,需要更新dis[t]=5.所以为
dis[]={dis[t]=5,dis[y]=3,dis[s]=9}
5、找了最小的dis[y],加入到T={x,w,v,u,y},wv在T里,所以只看zt dis[t]=4+dis[y]=7 dis[z]=10+dis[y]=13,所以现在的dis[]={dis[t]=5,dis[s]=9,dis[z]=13},找到最小的是dis[t],将t加入T中
6、T[]={x,w,v,u,y,t},和t直连的是uvzys,排除uvy,看z,s .dis[s]=1+dis[t]=6,dis[z]=2+dis[t]=2+5=7,需要更新,现在dis[]={dis[s]=6,dis[z]=7},找出最小的是dis[s],加入T
7、T[]={x,w,v,u,y,t ,s }与s直连的是t和u都在T中,所以不需要更新
8、剩下就是z了,也不需要更新,直接加入。
最后,排下dis数组。
dis[]={dis[w]=1,dis[v]=2,dis[u]=3,dis[y]=3,dis[t]=5,dis[s]=6,dis[z]=7}
得到这个数组后,填下答案就可以了。
| 目的 | 下一跳 | 代价 |
| s | ||
| t | ||
| u | ||
| v | ||
| w | W | 1 |
| y | ||
| z |
W是第二个加入的,属于直连边,代价是1,题目已经给出
v是通过W加入的,所以从x到V的下一跳是W,代价为1
| 目的 | 下一跳 | 代价 |
| s | ||
| t | ||
| u | ||
| v | W | 2 |
| w | W | 1 |
| y | ||
| z |
y是第四个加入的,是通过V加入的,所以下一跳 ,x -> w -> V 代价是3
| 目的 | 下一跳 | 代价 |
| s | ||
| t | ||
| u | ||
| v | x -> w | 2 |
| w | W | 1 |
| y | x -> w -> v | 3 |
| z |
依次填入表就可以了。
| 目的 | 下一跳 | 代价 |
| s | x -> w -> v -> y -> t | 6 |
| t | x -> w -> v -> u | 5 |
| u | x -> w -> v | 3 |
| v | x -> w | 2 |
| w | W | 1 |
| y | x -> w -> v | 3 |
| z | x -> w -> v -> y -> t | 7 |
标准答案:
| 目的 | 下一跳 | 代价 |
| s | W | 6 |
| t | W | 5 |
| u | W | 3 |
| v | W | 2 |
| w | W | 1 |
| y | W | 3 |
| z | W | 7 |
做题还是得细心,每一步都不要想当然!