群体智能之蜘蛛猴优化算法(SMO)
![]()
获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 第四章 蜘蛛猴优化算法
- 4.1 蜘蛛猴优化
- 4.1.1 动机
- 4.1.1.1 裂变融合社会结构的出现
- 4.1.1.2 蜘蛛猴的觅食行为
- 4.1.1.3 社会组织与行为
- 4.1.1.4 交流
- 4.1.2 蜘蛛猴优化过程
- 4.2 SMO分析
- 4.3 SMO参数
- 4.4 SMO性能分析
- 4.5 求解案例
- 4.6 结论
- 参考文献
第四章 蜘蛛猴优化算法
群居生物的觅食行为一直是优化算法研究的热点问题。蜘蛛猴优化(Spider Monkey Optimization,SMO)是一种全局优化算法,灵感来自于蜘蛛猴在觅食过程中的裂变融合社会(Fission-Fusion social,FFS)结构。SMO巧妙地描述了群体智能的两个基本概念:自组织和分工。SMO作为一种基于群体智能的算法,近年来得到了广泛的应用,并被应用于许多工程优化问题中。这一部分详细介绍了蜘蛛猴优化算法。为了更好地理解SMO过程的工作原理,给出了一个SMO过程的数例。
4.1 蜘蛛猴优化
蜘蛛猴优化(SMO)算法是近年来出现的一种基于群体智能的优化算法[1, 2],更新方程是基于可能解之间的欧氏距离,该算法已广泛应用于求解复杂的优化问题。在[3]中,Dhar和Arora应用蜘蛛猴优化算法(SMO)设计和优化了一个模糊规则库;Sharma等人[4]将SMO应用于IEEE-14、30和33测试总线系统中,在适当分配3和5个电容器的情况下,解决最优电容器配置和尺寸问题;Wu等人[5]将SMO用于稀疏线性阵列的合成。利用SMO算法对扩展稀疏子阵中所有元素的幅值和位置进行优化,从而在一组实际约束条件下降低整个阵列的旁瓣电平;Cheruku等人设计了用于糖尿病数据规则挖掘任务的SM-RuleMiner[6]。SMO还被用于合成线性天线阵的阵列因子,并为无线应用优化设计了一种E形贴片天线[7]。
下面将详细介绍蜘蛛猴优化算法的动机和工作原理。
4.1.1 动机
4.1.1.1 裂变融合社会结构的出现
裂变融合社会的概念是生物学家“汉斯·库默”在解释最复杂的哺乳动物阿拉伯狒狒的社会组织时提出的。由于季节变化导致食物短缺时,母系群体成员之间的食物竞争导致分裂成许多群体,然后融合成一个单一的群体。当食物供应充足时,群体是最大的,而在最小的群体中,食物短缺处于顶峰。裂变部分表现了蜘蛛猴的觅食行为,融合是将较小的群体组合成较大的群体。
4.1.1.2 蜘蛛猴的觅食行为
蜘蛛猴生活在中美洲和南美洲的热带雨林中,北至墨西哥[8]。蜘蛛猴是世界最聪明的猴子之一。它们被称为蜘蛛猴,因为当它们通过尾巴挂起来的时候看起来像蜘蛛[9]。蜘蛛猴总是喜欢生活在一个称为父群的单元组中。根据食物的稀缺性或充足性,它们会自动拆分或合并。它们之间通过手势、姿势和叫声进行交流。群体组成(Group composition)是这个结构中的一个动态属性。
4.1.1.3 社会组织与行为
蜘蛛猴的社会组织和行为可以通过以下事实来理解:
- 蜘蛛猴生活在一个大约40-50只个体的群体中;
- 这个群落里的所有个体在白天时都以小组的形式朝不同的方向觅食,晚上每个个体都在自己的栖息地分享觅食的经验。
- 领头的母蜘蛛猴决定觅食路线;
- 如果领头没有找到足够的食物,她就把小组分成更小的小组,这些小组分别觅食;
- 社会中的个体可能不会因为彼此之间的相互宽容而在一个地方被注意到。当他们接触时,他们的手势反映出他们实际上是一个大群体的一部分。
4.1.1.4 交流
蜘蛛猴通过位置和姿势分享它们的意图和观察结果。在很远的距离,它们通过特定的声音相互交流,如大叫或鸣叫。每只猴子都有自己可辨别的声音,其他小组成员可以通过这些声音辨别出那只猴子。
以上讨论的蜘蛛猴觅食行为如图1所示。
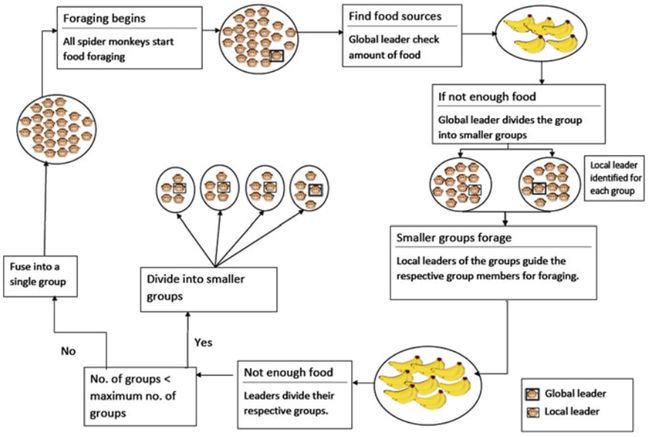
4.1.2 蜘蛛猴优化过程
SMO是一种元启发式技术,灵感来自于蜘蛛猴的智能觅食行为。蜘蛛猴的觅食行为是基于分裂融合的社会结构。该算法的特点依赖于一个群体的社会组织,在这个群体中,女性领导者决定是分裂还是合并。整个团队的领导者在这里被命名为全局领导者,而小组织的领导者被称为为局部领导者。参考SMO算法,食物短缺现象被定义为解不再改善。由于SMO是一种基于群体智能的算法,所以每个小群体都应该有一个最小数量的猴子。因此,在任何时候,如果进一步的裂变产生了至少一组少于最小数量的猴子,我们将其定义为融合时间。在SMO算法中,蜘蛛猴(SMO)表示一个可选解。SMO由六个阶段组成:局部领导者阶段、全局领导者阶段、局部领导者学习阶段、全局领导者学习阶段、局部领导者决策阶段和全局领导者决策阶段。接下来将解释SMO的所有这些阶段:
初始化:
在初始化阶段,SMO生成一个包含N个蜘蛛猴的均匀分布初始群体, SMi代表群体中的第 i个蜘蛛猴,每个 SMi按下式初始化:
S M i j = S M min j + U ( 0 , 1 ) × ( S M max j − S M min j ) (1) S{M_{ij}} = S{M_{\min j}} + U(0,1) \times \left( {S{M_{\max j}} - S{M_{\min j}}} \right)\tag 1 SMij=SMminj+U(0,1)×(SMmaxj−SMminj)(1)
其中SMminj和SMmaxj 是搜索空间中第 j维的下界和上界,U(0,1)是(0,1)内均匀分布的随机数。
局部领导者阶段(LLP):
这是SMO算法的一个重要阶段。在这里,所有的蜘蛛猴都有机会更新自己。蜘蛛猴基于其局部领导者和小组成员的经验更新其位置。在新的位置计算每个蜘蛛猴的适应度值,如果适应度高于其旧的位置,则更新,否则不更新。这里,位置更新方程为
S M n e w i j = S M i j + U ( 0 , 1 ) × ( L L k j − S M i j ) + U ( − 1 , 1 ) × ( S M r j − S M i j ) (2) SMne{w_{ij}} = S{M_{ij}} + U(0,1) \times \left( {L{L_{kj}} - S{M_{ij}}} \right) + U( - 1,1) \times \left( {S{M_{rj}} - S{M_{ij}}} \right)\tag 2 SMnewij=SMij+U(0,1)×(LLkj−SMij)+U(−1,1)×(SMrj−SMij)(2)
其中,SMij是第i个蜘蛛猴的第j维,LLkj代表第k组局部领导者的第j维,SMrj是从第r组中随机选择的蜘蛛猴的第j维,且r≠i,U(-1,1)是(-1,1)范围内均匀分布的随机数。
从公式(2)中可以清楚地看出,待位置更新的蜘蛛猴在保持自己的自信或坚持时,会被局部领导者吸引,最后一部分有助于在搜索过程中引入扰动,维持算法的随机性,从而避免过早停滞。这个阶段的完整位置更新过程见算法1,该算法中pr表示当前解的扰动率,其值一般位于[0.1,0.8] 。
for 每一个属于第 组的成员 do
for 每一个维度 do
if then
使用式(2)更新位置;
else
不更新位置,即 ;
end if
end for
end for
全局领导者阶段(GLP):
完成局部领导者阶段后,算法进入全局领导者阶段,这里基于某一选择概率进行解的更新,而选择概率是适应度的函数。从目标函数fi可以根据下式计算处适应度fiti:
 (3)
(3)
选择概率probi由轮盘赌选择确定,如果fiti是第i个蜘蛛猴的适应度,可以通过以下任一公式计算其在全局领导者阶段被选中的概率:
p r o b i = f i t n e s s i ∑ i = 1 N f i t n e s s i 或 p r o b i = 0.9 × f i t i max − f i t + 0.1 pro{b_i} = \frac{{fitnes{s_i}}}{{\sum\limits_{i = 1}^N {{\rm{ fitness}}{{\rm{ }}_i}} }}或pro{b_i} = 0.9 \times \frac{{fi{t_i}}}{{{{\max }_ - }fit}} + 0.1 probi=i=1∑Nfitnessifitnessi或probi=0.9×max−fitfiti+0.1
蜘蛛猴利用全局领导者的知识、临近SM的经验和自身的坚持来更新自己的位置。该阶段位置更新方程为
S M n e w i j = S M i j + U ( 0 , 1 ) × ( G L j − S M i j ) + U ( − 1 , 1 ) × ( S M r j − S M i j ) (4) SM{\rm{ne}}{{\rm{w}}_{ij}} = S{M_{ij}} + U(0,1) \times \left( {G{L_j} - S{M_{ij}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + U( - 1,1) \times \left( {S{M_{rj}} - S{M_{ij}}} \right)\tag 4 SMnewij=SMij+U(0,1)×(GLj−SMij)+U(−1,1)×(SMrj−SMij)(4)
其中GLj是全局领导者在第j维上的位置,该位置更新等式包含三部分:第一部分展示了父(当前)蜘蛛猴的持久性,第二部分将父蜘蛛猴朝全局领导者方向吸引,最后一项用于维持算法的随机性。在这个等式中,第二项用于加强对已确定的搜索空间的利用,第三项用于避免搜索过程早熟收敛,降低陷入局部最优的机会。该阶段的整个搜素过程见算法2。
count=0;
while count<种群大小 do
for 群内的每一个成员 do
if U(0,1)<probi then
count=count+1;
随机选择维度j∈{1,2,...,D};
随机选择蜘蛛猴SMr且r≠i;
使用式(4)进行位置更新;
end if
end for
end while
显然,算法2中更新解的机会取决于probi,因此高适应度的解相较于低适应度的解,有更多的机会更新其位置。此外,对已更新解应用贪婪选择方法,即对于已更新和原有的蜘蛛猴,只考虑适应度更优的解。
全局领导者学习阶段:
在此阶段,算法找出整个群体的最优解,被识别的蜘蛛猴被认为是群体的全局领导者。此外,检查全局领导者的位置,如果不更新它,那么与全局领导者关联的计数器(称为全局限制计数(global Limit Count, GLC))将增加1,否则将设置为0。
检查全局领导者的全局限制计数,并与全局领导者限制比较。
局部领导者学习阶段:
在算法的这一阶段中,通过对组内成员进行贪婪选择来更新局部领导者的位置。如果局部领导者没有更新其位置,那么与局部领导者关联的计数器local Limit Count (LLC)将增加1;否则计数器被设置为0。此过程应用于每个组,以找到其各自的局部领导者。
局部限制计数是一个计数器,它会递增,直到达到一个固定的阈值,称为局部领导者限制Local Leader Limit (LLL)。
局部领导者决策阶段:
在此阶段之前,已经确定了局部领导者和全局领导者。如果有任何局部领导者没有被重新组织到一个特定的边缘,也就是所谓的局部领导者限制,然后,该组所有成员通过随机初始化或通过公式(5)使用全局领导者的经验来更新他们的位置。按照一个被称为扰动率的概率pr应用公式(5)。
S M n e w i j = S M i j + U ( 0 , 1 ) × ( G L j − S M i j ) + U ( 0 , 1 ) × ( S M r j − L L k j ) (5) SMne{w_{ij}} = S{M_{ij}} + U(0,1) \times \left( {G{L_j} - S{M_{ij}}} \right) + U(0,1) \times \left( {S{M_{rj}} - L{L_{kj}}} \right)\tag 5 SMnewij=SMij+U(0,1)×(GLj−SMij)+U(0,1)×(SMrj−LLkj)(5)
从这个方程可以看出,当现有的局部领导者被耗尽(迭代LLL次没有更新)时,该组的解被排斥,而解被吸引向全局领导者,以改变现有的搜索方向和位置。基于pr,随机初始化解的某些维数,在解的现有位置引入扰动。这里局部领导者限制是检查局部领导者是否陷入局部极小值的参数,通常计算为DxN,其中D为维度,N为SM的总数。如果LLC大于LLL,则将LLC设置为零,并按照上面描述的方式初始化SM,以改进搜索空间的探索。
if 局部限制计数>局部领导者限制 then
局部限制计数=0;
for 每一个维度 do
if U(0,1)>pr then
执行式(1);
else
执行式(5);
end if
end for
end if
全局领导者决策阶段:
类似于局部领导者决策阶段,如果全局领导者没有被重新组织到一个特定的边缘,即全局领导者限制,那么全局领导者会将群体划分成更小的组或将组融合为一个单元组。这里全局领导者限制GLL是检查是否存在早熟的参数,一般取值范围为[n/2,2N]。如果全局领导者计数超过全局领导者限制,那么设置计数为0,同时比较组数与最大组数。如果现有的组数少于预定义的最大组数,那么全局领导者会进一步分组,否则通过组合形成单个父组。算法4中描述了分裂-融合过程。
if 全局限制计数>全局领导者限制
全局限制计数=0;
if 组数<MG then
分裂群体成组;
else
组合所有的组为一个组;
end if
更新局部领导者位置;
end if
算法5给出了SMO解决优化问题的完整工作机制。
Step1. 初始化种群、局部领导者限制、全局领导者限制和扰动率pr;
Step2. 评估种群;
Step3. 识别全局和局部领导者;
Step4. 局部领导者阶段位置更新(算法1);
Step5. 全局领导者阶段位置更新(算法2);
Step6. 通过全局领导者学习阶段进行学习;
Step7. 通过局部领导者学习阶段进行学习;
Step8. 局部领导者决策阶段位置更新(算法3);
Step9. 全局领导者决策阶段决定分裂或融合(算法4);
Step10. 如果满足终止条件则停止,并将全局领导者位置声明为最优解,否则跳转至Step4。
4.2 SMO分析
在寻找最优解的同时,SMO更好地平衡了利用和探索。局部领导者阶段用于探索搜索区域,在这个阶段,所有的组成员都会更新他们的位置,并且在维数上有很高的扰动。而全局领导者阶段促进了利用,在这个阶段,更好的候选人有更多的机会更新他们的位置。该特性使SMO在基于搜索的优化算法中成为较好的候选对象。SMO还拥有一种内置的停滞检查机制。局部领导者学习阶段和全局领导者学习阶段,用于检查搜索过程是否停滞不前。在停滞的情况下(在局部或全局层面),局部领导者和全局领导者的决策阶段将工作。局部领导者决策阶段创建了一个额外的探索,而在全局领导者决策阶段,则做出关于裂变或聚变的决策。因此,在保持收敛速度的同时,SMO可以更好地平衡探索和利用。
4.3 SMO参数
SMO主要有四个控制参数:局部领导者限制(LLL)、全局领导者限制(GLL)、最大组数(MG)和扰动率pr。下面给出了参数的建议设置:
- MG=N/10,通过这样设定,可以保证组中最少有10个蜘蛛猴;
- GLL∈[N/2,2N];
- LLL=DxN;
- pr∈[0.1,0.8]。
4.4 SMO性能分析
在[2]将SMO的性能与三种著名的元启发式算法,即人工蜂群算法(ABC)、差分进化算法(DE)和粒子群优化算法(PSO)进行了对比分析。通过对25个基准问题的测试和各种统计测试,得出的结论是SMO是一种具有竞争力的元启发式优化算法,在单峰、多峰、可分性和不可分性优化问题中具有良好的性能。对于连续优化问题,SMO比PSO、ABC或DE具有更好的可靠性。
4.5 求解案例
这一节描述了一个使用SMO的数值案例,逐步求解简单的优化问题f(x)=x12+x22。
考虑如下优化问题:
M i n i m i z e f ( x ) = x 1 2 + x 2 2 ; − 5 ≤ x 1 , x 2 ≤ 5 {\rm{Minimize }}f(x) = x_1^2 + x_2^2;\quad - 5 \le {x_1},{x_2} \le 5 Minimizef(x)=x12+x22;−5≤x1,x2≤5
SMO的控制参数如下:
种群大小N=20。
问题维度D=2.。
MG=N/10=2。
GLL∈[N/2,2N]=[10,40],取GLL=30。
LLL=DxN=2x20=40。
扰动率pr∈[0.1,0.8],取pr=0.7。
初始化:
在[-5,5]范围内随机初始化20个食物源的位置(蜘蛛猴)。
| SM number | x1 | x2 | SM number | x1 | x2 |
|---|---|---|---|---|---|
| 1 | 1.4 | 1.2 | 11 | 0.1 | -0.9 |
| 2 | -2.4 | -2.5 | 12 | 0.3 | 0.3 |
| 3 | 0.6 | -0.4 | 13 | -0.4 | 0.6 |
| 4 | 0.3 | 1.5 | 14 | 0.5 | 0.7 |
| 5 | -0.7 | 1.9 | 15 | 1.3 | -1.5 |
| 6 | 2.9 | 3.2 | 16 | -1.1 | 0.8 |
| 7 | 1.6 | -0.9 | 17 | 0.8 | -0.9 |
| 8 | 0.8 | 0.2 | 18 | 0.4 | -0.2 |
| 9 | -0.5 | 0.1 | 19 | -0.6 | 0.3 |
| 10 | 0.3 | 0.2 | 20 | 0.8 | 1.6 |
对应的函数值和适应度值如下:
| SM number | fi(x) | fiti(x) | SM number | fi(x) | fiti(x) |
|---|---|---|---|---|---|
| 1 | 3.4 | 0.227 | 11 | 0.82 | 0.549 |
| 2 | 12.01 | 0.077 | 12 | 0.18 | 0.847 |
| 3 | 0.52 | 0.658 | 13 | 0.52 | 0.658 |
| 4 | 2.34 | 0.299 | 14 | 0.74 | 0.575 |
| 5 | 4.1 | 0.196 | 15 | 3.94 | 0.202 |
| 6 | 18.65 | 0.051 | 16 | 1.85 | 0.351 |
| 7 | 3.37 | 0.229 | 17 | 1.45 | 0.408 |
| 8 | 0.68 | 0.595 | 18 | 0.2 | 0.833 |
| 9 | 0.26 | 0.794 | 19 | 0.45 | 0.690 |
| 10 | 0.13 | 0.885 | 20 | 3.2 | 0.238 |
这里由于最大的适应度为0.885,对应的是第10个蜘蛛猴,因此第10个蜘蛛猴就为全局领导者,在此阶段只有单一一个组,所以该蜘蛛猴也是局部领导者。
位置更新阶段:
局部领导者阶段
在此阶段,所有的蜘蛛猴都有机会更新其位置,更新公式见(2)。
更新第一个蜘蛛猴(i=1)
对于第一个维度j=1,生成一个随机数U(0,1),设U(0,1)=0.3。由于U(0,1)≥pr(=0.7)为false,因此SMnew11=SM11。
对于j=2,设U(0,1)=0.8,由于pr≤0.8,SM12将进行更新。
如果随机选择邻域解索引r=6,且U(-1,1)=-0.7,则SMnew12=1.2+0.8(0.2-1.2)+(-0.7)(3.2-1.2)=-1
所以新解x1=(1.4,-1)。
计算其函数值和适应度值,f1(SMnew1)=2.96,fit(SMnew1)=0.252。
基于适应度值对SMnew1和SM1进行贪婪选择,由于0.252>0.227,所以新解SMnew1更优,所以SM1=(1.4,-1)。
同样对其他解进行类似的更新。
| SM number | Updated dimension j | SMnew | SMnew | fi (x) | Fiti |
|---|---|---|---|---|---|
| 1 | 2 | 1.4 | -1 | 2.96 | 0.252 |
| 2 | 1 | -1.56 | -2.5 | 8.6836 | 0.1032 |
| 3 | 2 | 0.6 | 0.12 | 0.3744 | 0.727 |
| 4 | – | 0.3 | 1.5 | 2.34 | 0.299 |
| 5 | 1 | -0.34 | 1.5 | 2.366 | 0.2971 |
| 6 | – | 0.69 | 3.2 | 10.716 | 0.0854 |
| 7 | 1 | 1.6 | -0.9 | 3.37 | 0.2288 |
| 8 | – | 0.4 | 0.2 | 0.2 | 0.8333 |
| 9 | – | -0.5 | 0.1 | 0.26 | 0.7937 |
| 10 | – | 0.3 | -0.2 | 0.13 | 0.885 |
| 11 | 2 | 0.1 | 0.31 | 0.106 | 0.9041 |
| 12 | 1 | 0.42 | 0.3 | 0.266 | 0.7896 |
| 13 | – | -0.4 | 0.6 | 0.52 | 0.6579 |
| 14 | 2 | 0.5 | -0.26 | 0.318 | 0.759 |
| 15 | – | 1.3 | -1.5 | 3.94 | 0.2024 |
| 16 | 2 | -1.1 | -0.165 | 1.237 | 0.447 |
| 17 | 2 | 0.8 | -0.33 | 0.749 | 0.5718 |
| 18 | 2 | 0.4 | 0.14 | 0.18 | 0.8477 |
| 19 | – | -0.6 | 0.3 | 0.45 | 0.6897 |
| 20 | 2 | 0.8 | -0.142 | 0.66 | 0.6024 |
对于全局领导者阶段,需要根据适应度向量计算概率函数,即probi=0.9xfiti/max_fit+0.1,这里max_fi=0.9041,对应着第11个解。下表列出了适应度概率。
| SM | probi | SM | probi |
|---|---|---|---|
| 1 | 0.38968 | 11 | 1 |
| 2 | 0.202732 | 12 | 0.886019 |
| 3 | 0.823703 | 13 | 0.754916 |
| 4 | 0.397644 | 14 | 0.855558 |
| 5 | 0.395753 | 15 | 0.301482 |
| 6 | 0.185013 | 16 | 0.544973 |
| 7 | 0.327762 | 17 | 0.669207 |
| 8 | 0.929521 | 18 | 0.943856 |
| 9 | 0.890101 | 19 | 0.786572 |
| 10 | 0.980987 | 20 | 0.699668 |
全局领导者阶段
在此阶段,蜘蛛猴将基于上面计算的概率probi按照式(4)进行更新,更新数量取决于种群大小。这里只展示第8和第17只蜘蛛猴的更新过程。需要注意的是,每个被选择的解只需要更新其一个维度。
更新第8个蜘蛛猴(i=8)
prob8=0.929521,设U(0,1)=0.6 设随机选择的维度为j=2。 对SM8进行全局领导者阶段位置更新,得到SMnew8=(0.4,-0.75),计算得到函数值和适应度值分别为f8(x)=0.7225和fit8=0.5805。由于0.5805<0.8333,所以不对SM8进行更新。 更新第17个蜘蛛猴(i=17) prob17=0.6692,设U(0,1)=0.52 设随机选择的维度为j=1。 对SM17进行全局领导者阶段位置更新,得到SMnew17=(-0.264,-0.33),计算得到函数值和适应度值分别为f17(x)=0.1785和fit17=0.8484。由于0.8484>0.5718,所以对SM17进行更新,得到SM17=(-0.264,-0.33)。 第一轮过后(所有解都有机会更新其位置),蜘蛛猴的新位置如下: 在全局领导者阶段的第一轮,一共有12个解得到了更新,根据本阶段的终止条件,更新次数应该等于种群中蜘蛛猴的个数,因此开始下一轮更新蜘蛛猴。第二轮过后,蜘蛛猴更新后的位置如下: 目前在此阶段,蜘蛛猴的总更新次数为20,所以该阶段停止。很显然,具有更高适应度的解将有更多的机会更新其位置,从而提高算法的利用能力。 全局领导者学习阶段 局部领导者学习阶段 局部领导者学习阶段决定了小组的局部领导者。与全局领导者学习阶段类似,所有解的适应度都将相互比较。如果局部领导者获得更好的位置,则将局部限制计数设置为0,否则将计数增加1。这里我们只有一个组,所以第9个蜘蛛猴既是全局领导者,也是局部领导者。局部限制计数被设置为0,因为已更新了局部领导者。 局部领导者决策阶段 全局领导者决策阶段 在此阶段,将监视全局领导者的位置,如果达到全局领导者限制(本例中为30)次没有更新,则将种群划分为更小的组。如果子组的数量达到其最大计数(本例中为=2),则将所有子组组合成一个组。在做出决定后,将全局限制计数设置为0,并更新局部领导者的位置。 为了解释全局领导者决策阶段的作用,考虑这样一个情况:对于某个迭代,全局限制计数为31,然后将该组划分为两个子组。解SM1-SM10属于第一组,而SM11-SM20属于第二组。假设群体由下表表示: 由于第9个蜘蛛猴的适应度在第一组的所有蜘蛛猴中最高,因此它被指定为第一组的局部领导者,即LL1=(-0.4,0.1)。其次,第二组中第19蜘蛛猴的适应度最高,被认为是第二组的局部领导者,即LL2=(-0.4,0.3)。对于两个局部领导者,局部限制计数都被设置为0。 也可以看出,第9个蜘蛛猴的适应度在群体的所有成员中是最好的,因此第9个蜘蛛猴被认为是群体的全局领导者,即GL=(-0.4,0.1)。由于执行了全局领导者决策,全局限制计数变为0。 经过全局领导者决策阶段后,再由局部领导者阶段和其他阶段以类似的方式对群体进行更新。此过程将迭代地继续,直到达到终止条件。 本部分中,讨论了一种基于群体智能的算法-蜘蛛猴优化算法,该算法从蜘蛛猴的社会行为中得到启发。在SMO中,局部领导者阶段和全局领导者阶段有助于利用搜索空间,而探索则通过局部领导者决策阶段和全局领导者决策阶段完成。SMO性能分析表明,SMO在可靠性、有效性和精度方面超过了ABC、DE和PSO。然而,SMO中存在大量依赖于用户的参数,是需要进一步研究的问题。自适应参数调整有助于提高算法的鲁棒性和可靠性。仅仅在5年内,就有大量关于SMO的开发和应用的出版物,这表明SMO具有成为高效优化器的巨大潜力。 备注:SMO代码(C++,Python和Matlab)可在http://smo.scrs.in/下载。
SM number
j
SMnewij
SMnewij
fi (x)
Fiti
1
–
1.4
-1
2.96
0.252525
2
–
-1.56
-2.5
8.6836
0.103267
3
2
0.6
0.4
0.52
0.657895
4
–
0.3
1.5
2.34
0.299401
5
1
0.1
1.5
2.26
0.306748
6
–
0.69
3.2
10.7161
0.085353
7
2
1.6
-0.3
2.65
0.273973
8
1
1.1
0.2
1.25
0.444444
9
1
-0.8
0.1
0.65
0.606061
10
2
0.3
-0.9
0.9
0.526316
11
2
0.1
-0.4
0.17
0.854701
12
1
0.3
0.3
0.18
0.847458
13
1
-0.8
0.6
1
0.5
14
1
-0.2
-0.26
0.1076
0.902853
15
–
1.3
-1.5
3.94
0.202429
16
–
-1.1
-0.165
1.237225
0.446982
17
1
-0.264
-0.33
0.178596
0.848467
18
1
0.45
0.14
0.2221
0.818264
19
–
-0.6
0.3
0.45
0.689655
20
–
0.8
-0.142
0.660164
0.60235
SM number
j
SMnewij
SMnewij
fi(x)
Fiti
1
–
1.4
-1
2.96
0.252525
2
–
-1.56
-2.5
8.6836
0.103267
3
–
0.6
0.4
0.52
0.657895
4
–
0.3
1.5
2.34
0.299401
5
–
0.1
1.5
2.26
0.306748
6
–
0.69
3.2
10.7161
0.085353
7
–
1.6
-0.3
2.65
0.273973
8
–
1.1
0.2
1.25
0.444444
9
1
-0.4
0.1
0.17
0.854701
10
1
-0.8
-0.9
1.45
0.408163
11
1
1.2
-0.4
1.6
0.384615
12
1
1.8
0.3
3.33
0.230947
13
–
-0.8
0.6
1
0.5
14
2
-0.2
0.7
0.53
0.653595
15
–
1.3
-1.5
3.94
0.202429
16
–
-1.1
-0.165
1.237225
0.446982
17
2
-0.264
-0.8
0.709696
0.584899
18
2
0.45
-0.3
0.2925
0.773694
19
1
-0.4
0.3
0.25
0.8
20
–
0.8
-0.142
0.660164
0.60235
’
全局领导者学习阶段决定了群体的全局领导者。所有解的适应度将相互比较,如果全局领导者获得更好的位置,则将全局限制计数设置为0,否则将其增加1。由于第9个蜘蛛猴的适应度在更新后的群体中是最好的,所以它成为了全局领导者。此外,全局限制计数将被设置为0,因为全局领导者已经更新。
根据我们的参数设置,局部领导者限制是40。因为局部限制计数=0<40,所以此阶段不执行。
Group number,SMnumber
SMnewij
SMnewij
fi (x)
Fiti
K1, SM1
1.4
-1
2.96
0.252525
K1, SM2
-1.56
-2.5
8.6836
0.103267
K1, SM3
0.6
0.4
0.52
0.657895
K1, SM4
0.3
1.5
2.34
0.299401
K1, SM5
0.1
1.5
2.26
0.306748
K1, SM6
0.69
3.2
10.7161
0.085353
K1, SM7
1.6
-0.3
2.65
0.273973
K1, SM8
1.1
0.2
1.25
0.444444
K1, SM9
-0.4
0.1
0.17
0.854701
K1, SM10
-0.8
-0.9
1.45
0.408163
K2, SM11
1.2
-0.4
1.6
0.384615
K2, SM12
1.8
0.3
3.33
0.230947
K2, SM13
-0.8
0.6
1
0.5
K2, SM14
-0.2
0.7
0.53
0.653595
K2, SM15
1.3
-1.5
3.94
0.202429
K2, SM16
-1.1
-0.165
1.237225
0.446982
K2, SM17
-0.264
-0.8
0.709696
0.584899
K2, SM18
0.45
-0.3
0.2925
0.773694
K2, SM19
-0.4
0.3
0.25
0.8
K2, SM20
0.8
-0.142
0.660164
0.60235
4.6 结论
参考文献