群体智能优化算法之和声搜索(Harmony Search,HS)-附源码
![]()
获取更多资讯,赶快关注上面的公众号吧!
文章目录
- 一种新的启发式优化算法:和谐搜索(Harmony Search,HS)
- 启发
- 和声记忆库(HM)
- 创作新的和声
- 音调调节
- 和声记忆库更新
- 和声搜索算法流程
- 算法分析和收敛性证明
- 参数设置
- 代码实现
一种新的启发式优化算法:和谐搜索(Harmony Search,HS)
当听一段优美的古典音乐时,谁曾想过演奏音乐与寻找解决复杂优化问题的最佳方案之间有什么联系呢?
韩国的Zong Woo Geem就发现了这种有趣的联系,于2001年提出了和声搜索算(Harmony Search,HS)法,是对音乐家通过反复调整不同乐器音调使之最终达到最美和声这一过程的模拟。
启发
和声搜索是一种基于音乐的元启发式优化算法。它的灵感来自于这样一种观察,即音乐的目的是寻求一种完美的和音状态。在音乐中努力寻找和音类似于在优化过程中寻找最优性。换句话说,一个爵士音乐家的即兴创作过程可以比作优化中的搜索过程。一方面,完美悦耳的和声是由听觉审美标准所决定的。音乐家总是想创作出完美和音的音乐作品。另一方面,优化问题的最优解应该是在给定目标和约束条件下的最优解。这两种过程都是为了生产出最好或最优的。
所以音乐演奏寻求由审美评价确定的最佳状态(美妙的和音),正如优化算法寻求由目标函数评价确定的最佳状态(全局最优-最小成本或最大效益)。审美评价是由乐器演奏的声音集合决定的,就像目标函数评价是由各个变量的值决定的一样;审美评价更高的声音可以通过一次又一次的练习来改进,就像更优的目标函数的评估值可以通过迭代来改进一样。
| 比较因素 | 优化过程 | 演奏过程 |
|---|---|---|
| 最优状态 | 全局最优 | 最美妙和声 |
| 评估方式 | 目标函数 | 审美标准 |
| 评估要素 | 变量值 | 乐器音调 |
| 处理单元 | 每次迭代 | 每次练习 |
和声记忆库(HM)
和声记忆库结构如图1所示,考虑一个由小提琴、萨克斯管和电子琴组成的爵士乐三重奏。初始时,记忆库中为随机的和声:(C,E,G),(C,F,A)和(B,D,G),这些和声通过审美评价进行排序。
和声记忆库可以表达为一个矩阵:
H M = [ x 1 1 x 2 1 ⋯ x n 1 f ( x 1 ) x 1 2 x 2 2 ⋯ x n 2 f ( x 2 ) ⋮ ⋯ ⋯ ⋯ ⋮ x 1 H M S x 2 H M S ⋯ x n H M S f ( x H M S ) ] \mathbf{H M}=\left[\begin{array}{cccc|c} x_{1}^{1} & x_{2}^{1} & \cdots & x_{n}^{1} & f\left(\mathbf{x}^{1}\right) \\ x_{1}^{2} & x_{2}^{2} & \cdots & x_{n}^{2} & f\left(\mathbf{x}^{2}\right) \\ \vdots & \cdots & \cdots & \cdots & \vdots \\ x_{1}^{H M S} & x_{2}^{H M S} & \cdots & x_{n}^{H M S} & f\left(\mathbf{x}^{H M S}\right) \end{array}\right] HM=⎣⎢⎢⎢⎡x11x12⋮x1HMSx21x22⋯x2HMS⋯⋯⋯⋯xn1xn2⋯xnHMSf(x1)f(x2)⋮f(xHMS)⎦⎥⎥⎥⎤
其中的每个和音 x i \mathbf{x}^{i} xi代表一个解向量,其每一个值 x d i x^{i}_{d} xdi表示第 d d d维的取值,对于连续问题,该值按照以下方式随机生成:
x d i = x d m i n + ( x d m a x − x d m i n ) × r a n d ( ) (1) x_{d}^i=x_{dmin}+\left(x_{dmax}-x_{dmin}\right) \times rand()\tag{1} xdi=xdmin+(xdmax−xdmin)×rand()(1)
其中 x d m a x x_{dmax} xdmax和 x d m i n x_{dmin} xdmin分别表示在第 d d d维上的最大、最小取值, r a n d ( ) ∈ [ 0 , 1 ] rand()\in [0,1] rand()∈[0,1]。
对于离散优化问题,则有:
x d i ∈ X i = { x d ( 1 ) , … , x d ( k ) , … , x d ( K d ) } (2) x_{d}^i \in \mathbf{X}_{i}=\left\{x_{d}(1), \ldots, x_{d}(k), \ldots, x_{d}\left(K_{d}\right)\right\}\tag{2} xdi∈Xi={xd(1),…,xd(k),…,xd(Kd)}(2)
其中 x d ( k ) x_{d}(k) xd(k)表示第 d d d维上的可选离散值。
创作新的和声
在创作阶段,同样以上面的三重奏为例,三种乐器产生一种新的和声,例如(C,D,A):小提琴从{C,C,B}中发生{C}音,萨克斯从{E,F,D}中发出{D}音,电子琴从{G,A,G}中发出{A}音。HM中每个音符都有相同的选择概率,如萨克斯的E,F和D音符都有33.3%的选择概率。
为了进一步理解,考虑如下的最小化问题,该问题的最优解向量是(2,3,1):
Min f ( x ) = ( x 1 − 2 ) 2 + ( x 2 − 3 ) 4 + ( x 3 − 1 ) 2 + 3 \operatorname{Min} f(x)=\left(x_{1}-2\right)^{2}+\left(x_{2}-3\right)^{4}+\left(x_{3}-1\right)^{2}+3 Minf(x)=(x1−2)2+(x2−3)4+(x3−1)2+3
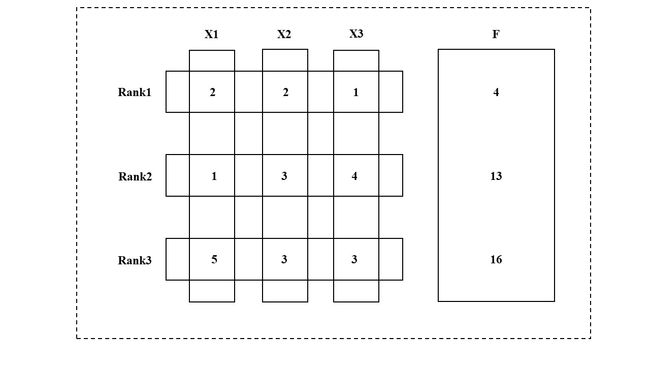
假设HM最初是由随机生成的变量值构成的,这些值根据目标函数的值进行排序,如图2a所示。之后,根据现在的HM创建了新的和声(1,2,3):x1从{2,1,5}中选择了{1},x2从{2,3,3}选择了{2},x3从{1,4,3}选择了{3},通过解码可以得到新和声对应的函数值为9,所以将该新和声加入到HM,并移除最差的{5,3,3},此时得到新的HM,如图2b所示。通过重复此过程,就能得到最优和音(2,3,1)。
当然,以上假设了全局最优解的所有部分最初都存在于HM中。当情况不是这样时,为了找到全局最优,和声搜索会启动一个参数和声记忆率Harmony Memory Considering Rate (HMCR) ∈ [ 0 , 1 ] \in[0,1] ∈[0,1],如果在[0,1]上均匀随机生成的随机数大于HMCR,则HS在可能的演奏范围内随机寻找音符,而不考虑和声记忆库HM。HMCR为0.95意味着在下一步,算法从HM中选择一个变量值的概率为95%。该过程可以通过下式表示:
x d i = { x i ∈ H M = { x d 1 , x d 2 , ⋯ , x d HMS } if r n d ≤ H M C R { = x d m i n + ( x d m a x − x d m i n ) × r a n d ( ) 连续 ∈ { x d ( 1 ) , ⋯ , x d ( k ) , ⋯ , x d ( K d ) } 离散 if r n d > H M C R (3) x_d^{i}=\left\{\begin{array}{l} x_{i} \in HM=\left\{x_{d}^{1}, x_{d}^{2}, \cdots, x_{d}^{\text {HMS }}\right\} & \text { if } rnd \leq H M C R \\ \left\{\begin{array}{l} =x_{dmin}+\left(x_{dmax}-x_{dmin}\right) \times rand() &\text { 连续 } \\ \in \left\{x_{d}(1), \cdots ,x_{d}(k), \cdots, x_{d}\left(K_{d}\right)\right\} &\text { 离散 } \end{array}\right.& \text { if } rnd \gt H M C R \end{array}\right. \tag{3} xdi=⎩⎨⎧xi∈HM={xd1,xd2,⋯,xdHMS }{=xdmin+(xdmax−xdmin)×rand()∈{xd(1),⋯,xd(k),⋯,xd(Kd)} 连续 离散 if rnd≤HMCR if rnd>HMCR(3)
音调调节
为了进一步改进解解的质量和避免局部优化,可能会引入另一种方式,这个方式模仿了每个乐器的音调调节来调整合奏。在计算中,音调调节机制被设计成在可能的取值范围内向邻域值移动。如果有6个可能的取值,如{1,3,4,6,7,9},在音调调节过程中{6}可以移动到邻域{4}或{7}。音调调节率(Pitch Adjusting Rate,PAR)取值为0.1意味着算法以0.1的概率选择邻域值(上下邻域各5%)。那么该过程可以表示为:
x d i = { x i ( k ± m ) 离散 x i ± Δ = x i ± F W × ϵ 连续 if r n d ≤ P A R (4) x_d^{i}=\left\{\begin{array}{l} x_{i}(k\pm m) & \text {离散 } \\ x_{i}\pm \Delta=x_{i}\pm FW \times \epsilon & \text {连续 } \end{array}\right. \text {if } rnd \leq PAR\tag{4} xdi={xi(k±m)xi±Δ=xi±FW×ϵ离散 连续 if rnd≤PAR(4)
其中, m ∈ { − 1 , 1 } m\in\{-1,1\} m∈{−1,1}, F W FW FW表示微调宽度(fret width), ϵ ∈ [ 0 , 1 ] \epsilon\in[0,1] ϵ∈[0,1]。
假设乐器(变量)的可选值集合为{C,D,E,F,G},HMCR为0.95,PAR为0.1,乐器在HM中已经存在{C,E,G}。在和声搜索算法的创作阶段,算法以95%的概率从{C,E,G}中,或5%的概率从{C,D,E,F,G}中均匀随机选择一个音符,当选择音符{E}后,{E}有10%的几率转移到{D}或{F}。
和声记忆库更新
如果新创作的和声(C,D,A)优于HM中任意一个现有的和声,则将该新创作的和声添加到HM中,并移除最差的和声(在上面的例子中,最差的为(B,D,G))。重复此过程,直到得到满意的结果(接近最优)。该过程可以表达为:
x N e w ∈ H M ∧ x W o r s t ∉ H M (5) \mathbf{x}^{N e w} \in \mathbf{H M} \quad \wedge \quad \mathbf{x}^{W o r s t} \notin \mathbf{H M}\tag{5} xNew∈HM∧xWorst∈/HM(5)
其中 x N e w \mathbf{x}^{New} xNew为新创作的和声, x W o r s t \mathbf{x}^{W o r s t} xWorst为和声记忆库中最差的和声。
和声搜索算法流程
基于上述过程的全新算法称为和声搜索(Harmony Search,HS),主要步骤如下:
- Step1:初始化和声记忆库(HM)。对于连续问题执行式(1),对于离散问题执行式(2);
- Step2:根据记忆库创作新的和声,包含创作和声和音调调节两个阶段。创作和声阶段以HMCR的概率从和声记忆库中随机选择,以1-HMCR的概率从可选值集合或范围内取值,对应公式(3);音调调节阶段以PAR的概率对创作和声阶段选出的音符进行邻域内搜索,对应公式(4);
- Step3:如果新的和声优于HM中的最小和声,则使用该新的和声替换HM中的最小和声(公式5);
- Step4:未满足停止准则,则跳转至Step2,否则结束。
算法分析和收敛性证明
为了证明和声搜索的收敛能力,考虑带参数的和声记忆库HM:
HM的大小(HM中和声数量)=HMS
乐器(变量)数量=N
乐器可能音符(变量值)的个数=L
乐器 i i i在HM中的最优音符个数为 H i H_i Hi
和声记忆率为 H r H_r Hr
最优和声(最优解向量)=(C,E,G)。
那么找到最优和声的概率 Pr ( H ) \operatorname{Pr}(\mathbf{H}) Pr(H)为:
Pr ( H ) = ⊆ N i = 1 [ H r H i H M S + ( 1 − H r ) 1 L ] \operatorname{Pr}(\mathbf{H})=\underset{i=1}{\overset{N}\subseteq}\left[H r \frac{H_{i}}{HMS}+(1-H r) \frac{1}{L}\right] Pr(H)=i=1⊆N[HrHMSHi+(1−Hr)L1]
由于音调调节率为可选操作,这里并不考虑。
初始时,HM中为随机的和声,如果在HM中所有乐器都不存在最优音符,即:
H 1 = H 2 = … . = H N = 0 H_{1}=H_{2}=\ldots .=H_{N}=0 H1=H2=….=HN=0
那么
Pr ( H ) = [ ( 1 − H r ) 1 L ] N \operatorname{Pr}(\mathbf{H})=\left[(1-H r) \frac{1}{L}\right]^{N} Pr(H)=[(1−Hr)L1]N
和声记忆率通常接近于1, 1 L ≤ 1 \frac{1}{L}\le1 L1≤1,所有一个很近于0的正小数的 N N N次方是很小的,也就是说此时找到最优和声的概率是非常小的。
但是,如果最优和声的模式(如(*,E,G),(C,*,G),(C,E,*))具有更优的适应度值,那么乐器 i i i在HM中的最优音符个数 H i H_i Hi将会随着迭代次数增加,从而找到最优和声的概率 Pr ( H ) \operatorname{Pr}(\mathbf{H}) Pr(H)也会增加。
如上所述,和声搜索本质上组合了现有启发式方法的结构。它保留了与禁忌搜索TS类似的过去向量(和声记忆库)的历史,并能够像模拟退火SA一样从计算的开始到结束改变适配率(和声记忆率),并以类似于GA的方式同时操纵多个向量。然而,遗传算法与HS的主要区别在于,HS从所有现有的向量(和声记忆库中的所有和声)中生成一个新向量,而遗传算法仅从两个现有的向量(父代)中生成一个新向量。此外,HS在生成新的向量时可以独立地考虑向量中的每个分量变量,而GA不能,因为它必须保持一个基因的结构。
参数设置
HS中涉及的参数主要为,和声记忆库大小HMS,和声记忆率HMCR,音调调节率PAR,最大创作数MI和微调宽度fw,下面一一分析这几个参数。
- HMS是算法中同时处理解向量的个数,可以理解为种群大小,该值通常根据优化问题取值为[20,200]。
- HMCR为从和声记忆库中随机选择一个音符的概率,那么1-HMCR就是从可选范围内随机取值的概率。和声记忆库HM因为其更新策略,通常其内的和声整体上比较美妙,所以应该尽可能地从记忆库中取值,这个“尽可能”一般就要求HMCR ∈ [ 0.7 , 0.95 ] \in[0.7,0.95] ∈[0.7,0.95]。但是HMCR又不能取值为1,这会导致算法无法进行探索而无法找到更优的解。
- PAR为音调调节概率,音调调节的目的就是对音符进行微调,从而跳出局部最优,该过程类似于遗传算法的变异操作。算法中通过PAR和FW控制调整的幅度,通常PAR ∈ [ 0.1 , 0.5 ] \in[0.1,0.5] ∈[0.1,0.5],FW ∈ [ 0.01 R a n g g e , 0.1 R a n g e ] \in[0.01Rangge,0.1Range] ∈[0.01Rangge,0.1Range],其中 R a n g e Range Range表示某一维度上的取值范围。
代码实现
下面结合代码具体说一下算法执行流程,java源码关注公众号后回复“和声”即可获取。
- 初始参数设置。主要设置和声记忆库大小HMS,最大创作次数 maxI,求解问题维度 numOfInstruments,微调宽度FW,和声记忆率HMCR,音调调节率PAR和目标函数 objectiveFun 等。
ObjectiveFun objectiveFun = new ObjectiveFun();
HSContinious hsContinious = HSContinious.builder().HMS(100).maxI(1000).numOfInstruments(2).FW(0.01).HMCR(0.7)
.PAR(0.25).objectiveFun(objectiveFun).build();
- 和声记忆库初始化。根据设定的记忆库大小,建立相应数量的和声,在目标函数自变量的取值范围内随机确定每个和声的音调组合,初始化结束后对和声进行评估,并按照由差到好的顺序排序。
/**
* 初始化和声记忆库
*/
@Override
public void initHM() {
// TODO Auto-generated method stub
// TODO Auto-generated method stub
System.out.println("**********和声记忆库初始化**********");
harmonyMemory = new ArrayList<>();
for (int i = 0; i < HMS; i++) {
harmonyMemory.add(new Harmony(new Composition(this.numOfInstruments, objectiveFun.getRange())));
}
for (Harmony harmony : harmonyMemory) {
harmony.setPerformence(this.objectiveFun.getObjValue(harmony.getComposition().getPitches()));
}
Collections.sort(harmonyMemory);
}
- 创作和声。对每个乐器(维度)进行遍历,以HMCR概率从和声记忆库中随机选择当前维度的值,再以PAR概率进行音调调节。
/**
* 创作和声
*/
@Override
public Harmony improviseHarmony() {
// TODO Auto-generated method stub
double rnd = random.nextDouble();
Range range = objectiveFun.getRange();
Harmony newHarmony = new Harmony(new Composition(this.numOfInstruments, range));
double[] newPitches = newHarmony.getComposition().getPitches();
for (int d = 0; d < numOfInstruments; d++) {
// 从和声记忆库中取值
if (rnd <= HMCR) {
newPitches[d] = harmonyMemory.get(random.nextInt(HMS)).getComposition().getPitches()[d];
// 音调调节
if (rnd <= PAR) {
newPitches[d] = newPitches[d]
+ (2 * random.nextDouble() - 1) * FW * (range.getHigh()[d] - range.getLow()[d]);
}
}
}
newHarmony.getComposition().setPitches(newPitches);
newHarmony.setPerformence(this.objectiveFun.getObjValue(newHarmony.getComposition().getPitches()));
return newHarmony;
}
- 更新迭代器。迭代次数加 。
public void incrementIter() {
iterator++;
}
- 循环。循环执行步骤 3~4,直到创作次数达到设定的最大创作次数。
while (this.iterator < maxI) {
Harmony improvisedHarmony = improviseHarmony();
updateHM(improvisedHarmony);
System.out.println(
"**********第" + iterator + "代最优解:" + harmonyMemory.get(harmonyMemory.size() - 1) + "**********");
incrementIter();
}
测试中使用的目标函数(最大化)方程和图像分别如下:
exp(-(x-4)^2-(y-4)^2)+exp(-(x+4)^2-(y-4)^2)+2*exp(-x^2-(y+4)^2)+2*exp(-x^2-y^2)
实验结果如下: