a^2+a^3=392怎么解? 分享一个有趣的解法
文章目录
- 出处
- 目标函数——转换问题
- 误差函数——评估model的性能
- 梯度下降——求解参数
- 代码
- 题外话——梯度下降为什么奏效
- 结语
- 参考
出处
原答案
a²+a³=392 怎么解? - 无线充电宝的回答 - 知乎
https://www.zhihu.com/question/357995704/answer/1293991286
知乎上偶然看到的,觉得很有意思,分享一下
刚好最近在学吴恩达的机器学习课程,看到作者的解法感觉耳目一新,简直完美契合所学课程,哈哈
首先作者给出了一些定义

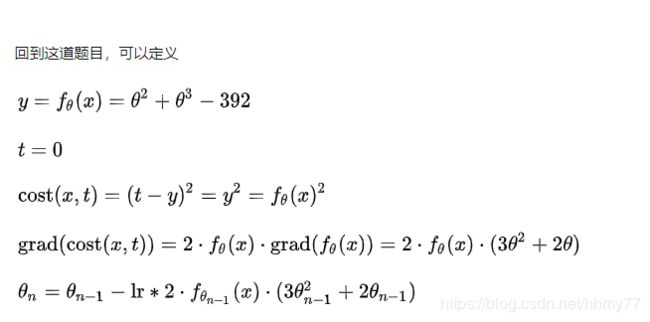
似乎和课程上学到的不太一样,没关系,我试着从初学者的角度来解析一下
目标函数——转换问题
问题是求 a 2 + a 3 = 392 a^2+a^3=392 a2+a3=392,我们移项过来变成 a 2 + a 3 − 392 = 0 a^2+a^3-392=0 a2+a3−392=0,现在我们的目的就是求出合适的a使得左边的式子等于0
下面我们定义目标函数,作者这里写成 f θ ( x ) f_\theta(x) fθ(x),其实写成什么符号都一样的
吴恩达使用的是h记号, h θ ( x ) = θ 2 + θ 3 − 392 h_\theta(x)=\theta^2+\theta^3-392 hθ(x)=θ2+θ3−392,目标函数的作用就是对于一组输入(训练集),调整函数的参数,然后尽可能地拟合输入预期的结果(训练集中y的值)
h是一个关于x的函数,x是输入,我们不需要额外的输入,所以把x都设为1,写成标准的形式应该是这样的
h θ ( x ) = θ 2 x 0 + θ 3 x 1 − 392 h_\theta(x)=\theta^2x_0+\theta^3x_1-392 hθ(x)=θ2x0+θ3x1−392,写成向量的形式是这样的 h θ ( x ) = θ ⃗ x ⃗ − 392 h_\theta(x)=\vec \theta \vec x-392 hθ(x)=θx−392,其中 θ ⃗ = [ θ 2 , θ 3 ] T \vec \theta=[\theta^2,\theta^3]^T θ=[θ2,θ3]T,而 x ⃗ = [ 1 , 1 ] T \vec x=[1,1]^T x=[1,1]T
那么输出呢?我们预期的输出 h θ ( x ) h_\theta(x) hθ(x)的结果尽可能的接近0。与之对应的就是上图的 t = 0 t=0 t=0,t这里的含义应该是target
再往下想一下,我们现在的目的是找到一组 θ ⃗ \vec \theta θ,使得 h θ ( x ) h_\theta(x) hθ(x)的结果尽可能的接近与0
目前为止我们还没有做任何的深入,仅仅是把问题转换成数学的形式,所以我们想要解决这个问题,仍然需要几个步骤。
误差函数——评估model的性能
现在有了目标函数,我们需要考虑如何评估这个函数(或者说这个model)的性能了
机器学习里面讲评估model的函数成为误差函数,误差函数当然是越小的越好,误差函数有多种model可以选择,一般有平方误差(MSE),交叉熵(用于分类问题,计算两个样本的相似度)等等。
详见 https://www.ibm.com/developerworks/cn/cognitive/library/cc-lo-talking-about-the-loss-function/index.html
我们这里误差函数使用的是平方误差,平方误差足够简单,下面是它的定义
M S E = 1 m ∑ i = 1 m ( y − y ^ ) 2 MSE=\frac{1}{m}\sum\limits_{i=1}^m(y-\hat y)^2 MSE=m1i=1∑m(y−y^)2
往下变为我们误差函数,误差函数是关于 θ ⃗ \vec \theta θ的函数
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y ^ ) 2 J(\theta)=\frac{1}{2m}\sum\limits_{i=1}^m(h_\theta(x_i)-\hat y)^2 J(θ)=2m1i=1∑m(hθ(xi)−y^)2
再展开
J ( θ ) = 1 2 m ∑ i = 1 m ( ( θ ⃗ x ⃗ − 392 ) − y ^ ) 2 J(\theta)=\frac{1}{2m}\sum\limits_{i=1}^m((\vec \theta \vec x - 392)-\hat y)^2 J(θ)=2m1i=1∑m((θx−392)−y^)2
J ( θ ) = 1 2 m ∑ i = 1 m ( ( θ 2 x 0 + θ 3 x 1 − 392 ) − y ^ ) 2 J(\theta)=\frac{1}{2m}\sum\limits_{i=1}^m((\theta^2x_0+\theta^3x_1 - 392)-\hat y)^2 J(θ)=2m1i=1∑m((θ2x0+θ3x1−392)−y^)2
在机器学习中我们有训练集,其中往往分为 x ⃗ \vec x x, y ⃗ \vec y y, x ⃗ \vec x x是作为输入,而 y ⃗ \vec y y是作为输出
例如房价预测中:
房子的衡量标准有:卧室,面积,楼层等等,这些都是房子的特征,也就是输入特征
而房价预测里面输出,也就是我们要预测的结果就是:房价
注意到我们有多个样本,所以平方误差函数上面需要求和,当我们设计出来一个model之后,使用平方误差函数求和,是输入训练集里面的所有特征,然后求model计算出来的结果和实际结果的平方和
现在看作者的定义就很清晰了,t=0没毛病。t-y还是y-t都是一样的

至于这里为什么分母是2m,而标准的定义是m,这里我先卖个关子,继续往下看
梯度下降——求解参数
目前为止我们有了model( h θ ( x ) h_\theta(x) hθ(x)),我们也有了评估model的方法(误差函数)
问题是我们如何调整model,求出参数,到达最好的效果呢?
这里我先不牵扯到太多的数学知识,直接引入梯度下降的概念
定义如下:
θ j + 1 : = θ j − α ∂ ∂ θ j J ( θ 0 , . . . , θ n ) \theta_{j+1}:=\theta_j-\alpha \frac{\partial}{\partial\theta_j}J(\theta_0,...,\theta_n) θj+1:=θj−α∂θj∂J(θ0,...,θn)
这里就是对误差函数求关于 θ i \theta_i θi的偏导,回头看误差函数的定义
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y ^ ) 2 J(\theta)=\frac{1}{2m}\sum\limits_{i=1}^m(h_\theta(x_i)-\hat y)^2 J(θ)=2m1i=1∑m(hθ(xi)−y^)2
嗯,对它求偏导是简单的
∂ J ∂ θ = 1 m ∑ i = 1 m ( h θ ( x i ) − y ^ ) ∂ h θ ( x ) θ \frac{\partial J}{\partial \theta}=\frac{1}{m} \sum\limits_{i=1}^m(h_\theta(x_i)-\hat y) \frac{\partial h_\theta(x)}{\theta} ∂θ∂J=m1i=1∑m(hθ(xi)−y^)θ∂hθ(x)
∂ h θ ( x ) θ = 2 θ + 3 θ 2 \frac{\partial h_\theta(x)}{\theta}=2\theta+3\theta^2 θ∂hθ(x)=2θ+3θ2, x x x都等于1之前已经说过了
那么结果 ∂ J ∂ θ 0 = 1 m ∑ i = 1 m ( h θ ( x i ) − y ^ ) ( 2 θ + 3 θ 2 ) \frac{\partial J}{\partial \theta_0}=\frac{1}{m} \sum\limits_{i=1}^m(h_\theta(x_i)-\hat y)(2\theta+3\theta^2) ∂θ0∂J=m1i=1∑m(hθ(xi)−y^)(2θ+3θ2)
你可能发现分母的2m被消掉2变成了m,这其实是一个无关紧要的技巧,只是为了让我们求导后式子变得更简洁一点
诸如给分母乘2除2,给结果加上某个数,在机器学习里面其实都是无关紧要的,这些好像积分得出来的结果加上的那个C,其实我们的目的就是求出主要的model,就算这些常数可能会引起model的bias,但是经过梯度下降以后,始终能找到一组合适的 θ ⃗ \vec \theta θ 来拟合数据
(我不知道上述的话对不对,只是我的直观感受 )
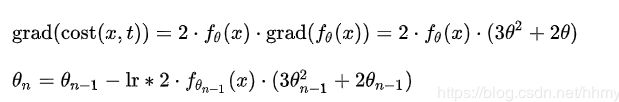
这里的grad就是对所有 θ \theta θ求偏导的结果,而下述的梯度下降中lr就是learning rate,吴恩达用 α \alpha α表示
这个2*lr和1/m都是常数,无所谓的
代码
下面是作者写的代码,很简洁,我稍微改动了一下
import random
def f(a):
return a ** 2 + a ** 3 - 392
def cost(a):
return f(a) ** 2
def grad(a):
return f(a) * (3 * a ** 2 + 2 * a)
def solve(eps, lr, max_iter=1000):
a = random.random()
i = 1
print('Initial value: ', a)
curr_cost = cost(a)
d_cost = abs(curr_cost)
while d_cost > eps and max_iter > 0:
# 梯度下降更新参数,乘不乘2无所谓的
a -= grad(a) * lr
print(f'Iteration {i}: {a}')
max_iter -= 1
prev_cost, curr_cost = curr_cost, cost(a)
d_cost = abs(curr_cost - prev_cost)
i += 1
return a if max_iter > 0 else None
eps = 0.001
lr = 0.00001
print('Solution: ', solve(eps, lr))
作者这里设置了一个eps控制误差,如果迭代到某一步变化没有超过eps的话,那么就不再迭代了
题外话——梯度下降为什么奏效
刚开始的时候觉得梯度下降效果很神奇,但是并不知道为什么奏效,关于梯度下降的原理,李宏毅老师在他的课上有讲到
https://www.youtube.com/watch?v=yKKNr-QKz2Q&feature=youtu.be
这里我再回忆一下
梯度下降背后的原理涉及到泰勒展开式,向量的知识,
梯度下降用于下山的说法很形象,其实就是使用梯度下降更新参数使得误差函数尽可能的小,此时model的性能也就越好
那么怎么才能正确的更新参数呢? 关键点就在于,对于当前参数,在足够小的范围内,选取那些能让误差函数值更小的参数来更新
请看图,对于 θ i \theta_i θi,我们指定一个足够小的范围(红圈),就可以在里面找到能让误差函数更小的参数
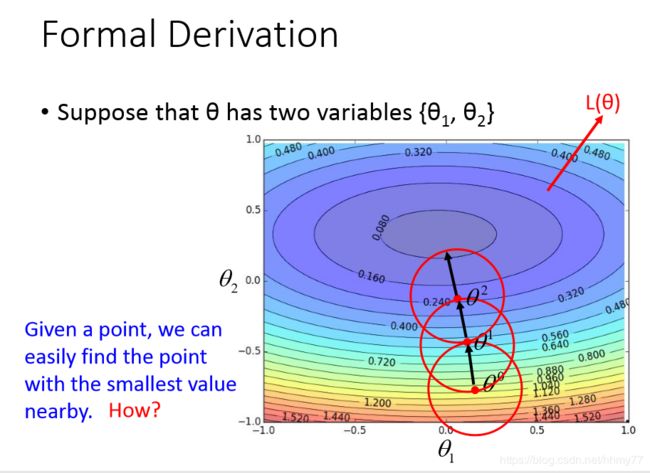
那么怎么找到这些合适的参数呢?
首先是泰勒展开式
泰勒展开式
对于某个在 x 0 x_0 x0无限可微的函数,我们可以用多项式展开来拟合这个函数在 x 0 x_0 x0这一点的值,多项式的项数越高,那么拟合的效果也就越好

例如:
拟合 f ( x ) = s i n ( x ) f(x)=sin(x) f(x)=sin(x)在 x 0 = π / 4 x_0=\pi/4 x0=π/4这一点的值
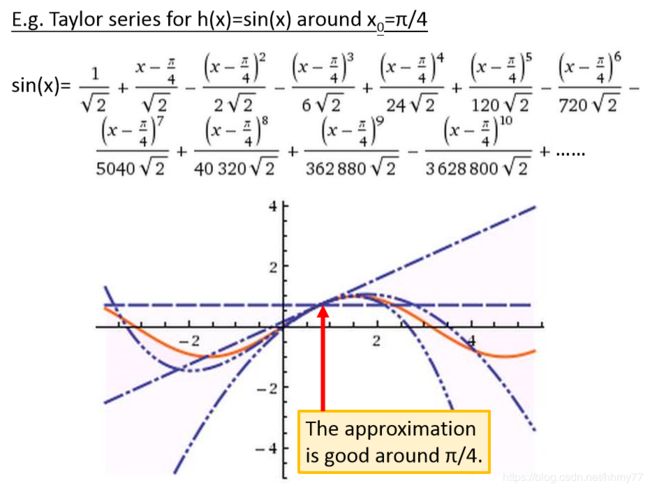
ok我们现在有一个工具,能够使用多项式来拟合某一点的函数值
然后我们尝试把泰勒展开应用到误差函数上,平方误差函数是无限可微的
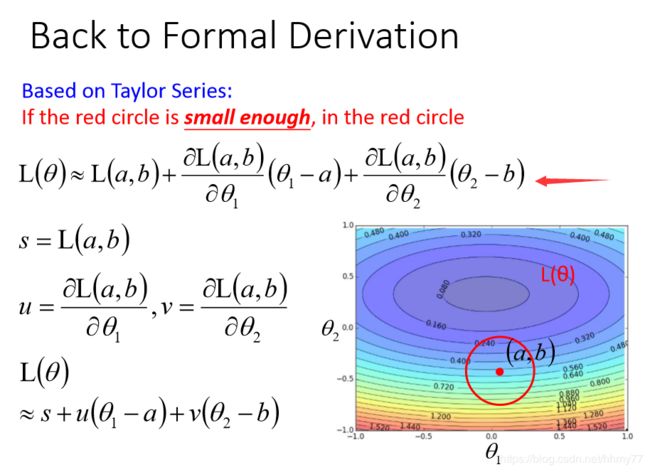
说明一下,PPT上误差函数是 L ( θ ) L(\theta) L(θ),它是关于 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2的函数。为了方便起见,我们就以上图的公式来讲解
这里我们把误差函数 L ( θ ) = L ( θ 1 , θ 2 ) L(\theta)=L(\theta_1,\theta_2) L(θ)=L(θ1,θ2)展开到一次项,就是上图所示的公式(这里是多变量展开)
我们对上图的参数做一个记号,分别是s,u,v
那么就可以化简为 L ( θ ) ≈ s + u ( θ 1 − a ) + v ( θ 2 − b ) L(\theta) \approx s+u(\theta_1-a)+v(\theta_2-b) L(θ)≈s+u(θ1−a)+v(θ2−b)的形式,
注意到上述 ( θ 1 − a ) (\theta_1-a) (θ1−a)与 ( θ 2 − b ) (\theta_2-b) (θ2−b)其实都是常数,那么我们可以用 Δ x 1 = ( θ 1 − a ) \Delta x_1= (\theta_1-a) Δx1=(θ1−a), Δ x 2 = ( θ 2 − b ) \Delta x_2= (\theta_2-b) Δx2=(θ2−b)来表示
公式改写为 L ( θ ) ≈ s + u Δ x 1 + v Δ x 2 L(\theta) \approx s+u\Delta x_1+v\Delta x_2 L(θ)≈s+uΔx1+vΔx2
由于泰勒公式展开有误差,实际上我们就获得了一个从当前参数开始划分的小范围,也就是上图红圈
ok我们现在要找到使得误差函数更小的参数,怎么找?
这里就涉及到向量的知识了,回顾一下向量内积
坐标系中两个向量相乘的时候,什么情况下得到的值是最小?
答案就是两个向量方向相反的时候
如下图

两个向量相反的时候,它们得到的值一定是最小的
但是目前为止我们都没有引入向量的概念,这个时候需要改写一下上述的公式
L ( θ ) ≈ s + u Δ x 1 + v Δ x 2 = s + A ⃗ T B ⃗ L(\theta) \approx s+u\Delta x_1+v\Delta x_2=s+\vec A^T \vec B L(θ)≈s+uΔx1+vΔx2=s+ATB,其中 A ⃗ = [ u , v ] T \vec A=[u,v]^T A=[u,v]T,而 B ⃗ = [ Δ x 1 , Δ x 2 ] T = [ θ 1 − a , θ 2 − b ] T \vec B=[\Delta x_1,\Delta x_2]^T=[ \theta_1-a,\theta_2-b]^T B=[Δx1,Δx2]T=[θ1−a,θ2−b]T
我们现在得到两个向量相乘了,然后呢? 我怎么知道新的 θ \theta θ怎么找?
先别急,总结一下我们目前获取到的条件和知识
- 泰勒开展能够拟合函数在某点上的值 => 图中红色圆圈
- 坐标系中了两个方向相反的向量相乘结果最小
- 已知 θ \theta θ的值 ( a , b ) (a,b) (a,b),想要找到新的 θ \theta θ,使得误差函数值更小
那么我们可以尝试分析一下:
对于上述例子,我们有 L ( θ ) ≈ s + A ⃗ B ⃗ L(\theta) \approx s+\vec A \vec B L(θ)≈s+AB,想要获取到更小的 θ \theta θ,则 A ⃗ \vec A A, B ⃗ \vec B B必须方向相反
方向相反用数学怎么表示?
即
A ⃗ = − η B ⃗ \vec A=-\eta \vec B A=−ηB
展开得
[ u , v ] = − η [ θ 1 − a , θ 2 − b ] [u,v]=-\eta [\theta_1-a,\theta_2-b] [u,v]=−η[θ1−a,θ2−b],这里 u = ∂ J ( θ ) ∂ θ 1 u=\frac{\partial J(\theta)}{\partial \theta_1} u=∂θ1∂J(θ), v = ∂ J ( θ ) ∂ θ 2 v=\frac{\partial J(\theta)}{\partial \theta_2} v=∂θ2∂J(θ)
继续展开得
[ θ 1 , θ 2 ] = [ a , b ] − η [ ∂ J ( θ ) ∂ θ 1 , ∂ J ( θ ) ∂ θ 2 ] [\theta_1,\theta_2]=[a,b]-\eta[\frac{\partial J(\theta)}{\partial \theta_1},\frac{\partial J(\theta)}{\partial \theta_2}] [θ1,θ2]=[a,b]−η[∂θ1∂J(θ),∂θ2∂J(θ)] (注: − η 小 于 0 -\eta小于0 −η小于0)
上面的式子是不是挺眼熟?
再回头看一下梯度下降的公式
θ j + 1 : = θ j − α ∂ ∂ θ j J ( θ 0 , . . . , θ n ) \theta_{j+1}:=\theta_j-\alpha \frac{\partial}{\partial\theta_j}J(\theta_0,...,\theta_n) θj+1:=θj−α∂θj∂J(θ0,...,θn)
你会发现它们其实是一样的,哈哈
那么按照这个方法选取的 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2,它们确实能够使 L ( θ ) L(\theta) L(θ)更加小,没毛病
结语
作者的原回答后面补充了很多知识,例如learning rate的选取大小,Adam算法使得learning rate能够自动变化等等等等很多知识
一道很简单的题目其实能延伸出来很多机器学习的知识
另外梯度学习的原理,很早就学习了,但是一直没有直观的感受,这次写博客感觉自己终于弄明白了,再次验证了费曼大神的那句话
What I cannot create,I do not understand
参考
https://www.zhihu.com/question/357995704/answer/1293991286
李弘毅的机器学习课程
吴恩达的机器学习课程
《深度学习中的数学》

