使用python(matplotlib和numpy)实现快速傅里叶变换(FFT),并画出频谱图和相位图
使用python(matplotlib和numpy)实现快速傅里叶变换(FFT),并画出频谱图和相位图
一.模块包的安装
win+R打开命令窗口,在命令窗口输入cm的,在终端D:,再输入cd D:\python\Python3.7\Scripts(这里是每个人的自己的安装目录)转到该安装目录下。
最后直接在命令窗口输入 pip install+需要安装的模块,例如本实验要安装的 pip install matplotlib
可以在idle输入import matplotlib查看是否安装成功
二.快速傅里叶变换(FFT)
FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
假设采样频率为Fs,信号频率fs,采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。
假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=sqrt(aa+bb)(某点处的幅度值An = A*(N/2)
下面以一个实际的信号来做说明:
假设我们有一个信号,频率为600Hz、相位为0度、幅度为5V的交流信号,用数学表达式就是如下:
y = 5 ∗ sin ( 2 ∗ p i ∗ 600 ∗ x ) y=5 * \sin (2 * p i * 600 * x) y=5∗sin(2∗pi∗600∗x)
采样频率为Fs=1400HZ,因为设置的信号频率分量为600赫兹,根据采样定理知采样频率要大于信号频率2倍,所以这里设置采样频率为1400赫兹(即一秒内有1400个采样点)
三.代码实现
代码使用的是python自带的idle编辑编译的。
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
mpl.rcParams['axes.unicode_minus']=False #显示负号
Fs=1400; #采样频率
Ts=1/Fs; #采样区间
x=np.arange(0,1,Ts) #时间向量,1400个
y=5*np.sin(2*np.pi*600*x)
N=1400
frq=np.arange(N) #频率数1400个数
half_x=frq[range(int(N/2))] #取一半区间
fft_y=np.fft.fft(y)
abs_y=np.abs(fft_y) # 取复数的绝对值,即复数的模(双边频谱)
angle_y=180*np.angle(fft_y)/np.pi #取复数的弧度,并换算成角度
gui_y=abs_y/N #归一化处理(双边频谱)
gui_half_y = gui_y[range(int(N/2))] #由于对称性,只取一半区间(单边频谱)
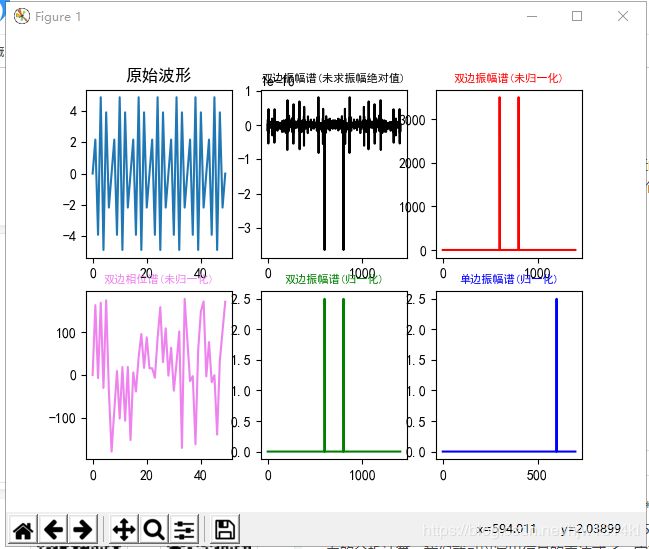
#画出原始波形的前50个点
plt.subplot(231)
plt.plot(frq[0:50],y[0:50])
plt.title('原始波形')
#画出双边未求绝对值的振幅谱
plt.subplot(232)
plt.plot(frq,fft_y,'black')
plt.title('双边振幅谱(未求振幅绝对值)',fontsize=8,color='black')
#画出双边求绝对值的振幅谱
plt.subplot(233)
plt.plot(frq,abs_y,'r')
plt.title('双边振幅谱(未归一化)',fontsize=8,color='red')
#画出双边相位谱
plt.subplot(234)
plt.plot(frq[0:50],angle_y[0:50],'violet')
plt.title('双边相位谱(未归一化)',fontsize=8,color='violet')
#画出双边振幅谱(归一化)
plt.subplot(235)
plt.plot(frq,gui_y,'g')
plt.title('双边振幅谱(归一化)',fontsize=8,color='green')
#画出单边振幅谱(归一化)
plt.subplot(236)
plt.plot(half_x,gui_half_y,'blue')
plt.title('单边振幅谱(归一化)',fontsize=8,color='blue')
plt.show()
1.原函数的幅度A=5,所以幅值等于5,与一图相同.
2.快速傅里叶变换后,因为我们频率是600HZ,大致在601这个点出现峰值,其他点趋近于零,An=A*(N/2)=3500,与二三图大致一样。
3.做归一化处理后,An=2.5,与五六图大致一样.