Ackerman阿克曼（后驱动）前轮舵机转向后轮电机驱动移动平台的建模及控制算法

运动建模

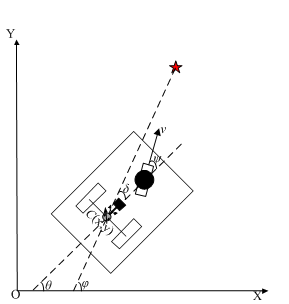
当机器运动特性为前轮转向后轮驱动时，通过与电机相连的两后轮的转动为其提供前行的动力，并且通过舵机调整前轮姿态从而改变其运动方向，如机器前轮转向后轮驱动方式示意图所示。

这种运动方式是通过与电机相连的两后轮的转动为其提供前行的动力，但是由于机器在执行曲线运动时，两后轮必然存在速度差。所以在两后轮间使用差速装置，从而通过机械方式调节两轮的速度。在曲线运动过程中，任意时刻下车轮的角速度相同，即${\omega }_l={\omega }_r$。以后轮中心点连线的中点$C(x,y)$为基准点，机器$\psi$，电机转速与两后轮速度的关系为：
$${\omega }_l+{\omega }_r=2{\omega }_h$$$$\frac{v_r}{R-\frac{\psi }{|\psi |}l}=\frac{v_l}{R+\frac{\psi }{|\psi |}l}$$
其中，${\omega }_h$为电机输出的转速，$v_l$和$v_r$分别为左右轮的线速度，$R$为基准点到旋转中心的距离（公转半径），l为左右轮到差速装置的距离。
则机器行驶的航向角速度${\omega }_c$为：
$${\omega }_c=\frac{v_c}{d}tan(\psi )$$
其中，$v_c$为驱动轮的线速度，$d$为基准点到前轮的间距。
在运动过程中，左右轮及基准点在做同轴运动，其角速度相同，可推出基准点线速度为左右轮线速度的一半。车体的线速度为：
$$v_c=\frac{v_l+v_r}{2}=\frac{r({\omega }_l+{\omega }_r)}{2}=r\cdot {\omega }_h$$
其中，$r$为轮半径。
则前轮驱动转向运动学模型为：
$$\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{c}cos\theta \\ sin\theta \\ 0\end{array}\right]\cdot v_c+\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\cdot {\omega }_c$$

两种基本运动行为

在前轮驱动转向运动方式下，驱动轮的偏角值域为$[-\pi /2,\pi /2]$。根据驱动轮不同的偏角值和转动方向，机器具备不同的两种运动行为，如图所示。

• a) 当$\psi \ne \pm \pi /2,0$时，机器做圆弧运动；
• b) 当$\psi =0$时，机器做直线运动。

仿真验证

直线运动仿真

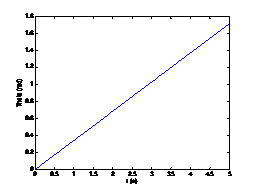
当初始位姿为[0, 0, 0, 0]，$\psi$ = 0时，机器在做直线运动，设定驱动轮半径为0.11m，角速度为1 rad/s，运行5s，得到仿真结果如图1-3所示。直行状态下姿态角不变，位置发生变化。

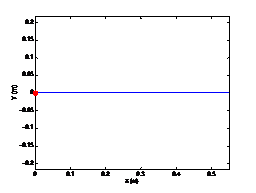
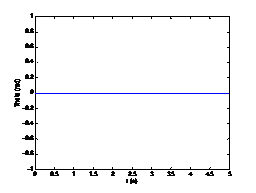
圆弧运动仿真

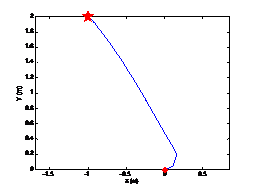
当初始位姿为[0, 0, 0, π/4]，ψ = π/4时，机器做圆弧运动，设定驱动轮线速度为1 rad/s，运行5s，得到仿真结果如图1-5所示。$\psi$为正值，机器左转做逆时针圆弧运动。

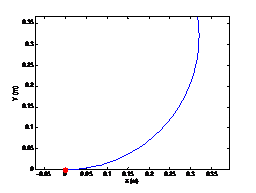
当初始位姿为[0, 0, 0, π/4]，$\psi$ = π/4时，机器做圆弧运动，设定驱动轮角速度为-1 rad/s，运行5s，得到仿真结果如图1-6所示。

原地旋转运动行为分析

动力分析

当机器需要执行原地旋转动作时，即令车体运动的线速度$v_c$=0, 角速度${\omega }_c$≠0。根据前轮舵机转向后轮电机驱动方式的运动学模型中线速度的表达方式：
$$v_c=\frac{v_l+v_r}{2}=\frac{r({\omega }_l+{\omega }_r)}{2}=r\cdot {\omega }_h$$
其中，${\omega }_h$为电机转速，电机的转动提供机器前行的动力。此时，${\omega }_h$的值也应为0，电机不再工作，车体没有了运动的动力来源，将保持静止无法运动。（受限于差速器结构特性，两后轮的转向不可以反向）

角度分析

当机器进行原地旋转时，需要将旋转中心移到后轮中心位置，此时前轮偏角需要为$\psi =\pi /2$，从运动模型公式中可知：
$${\omega }_c=\frac{v_c}{d}tan(\psi )$$
此时的角速度趋近于无穷大，车体坐标系下的左右分力为0，车体无法运动。
综上所述，通过动力和角度分析，这种前轮舵机转向后轮电机驱动方式与汽车类似，无法实现原地旋转的动作。（参考GB7258-2017第6.4条规定：“机动车方向盘的最大自由转动量应小于或等于：a）最大设计车速大于或等于100km/h的机动车：15°”；第6.6条规定:“三轮汽车、摩托车及轻便摩托车的转向轮向左或向右转角不允许大于45°。…”）
（在该规定下的最小转动半径为$R_{min}=d\approx 0.8m$）。

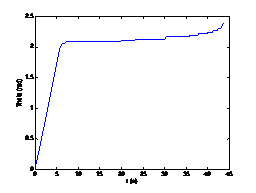
仿真结果分析

仿真结果分析，观察Theta值即姿态角（偏航角）的变化，可以发现每一个时刻下的增量都是无穷大。

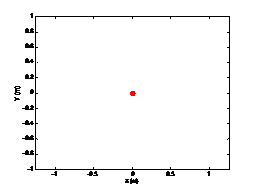
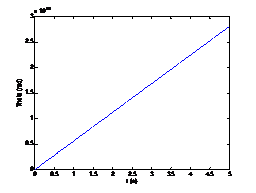
对控制的影响，在对前轮最大偏角限定后，缺少了原地旋转这一动作，要实现导航或控制只能通过进行圆弧运动与直线运动的组合来完成。当给定目标位置的距离大于最小转动半径时，尚可在不添加控制调节点的情况下到达；反之，则必须加入调整点。

综上所述，前轮舵机转向后轮电机驱动移动平台并不具备原地旋转的功能。

运动控制

控制原理

舵机调向，电机调速。

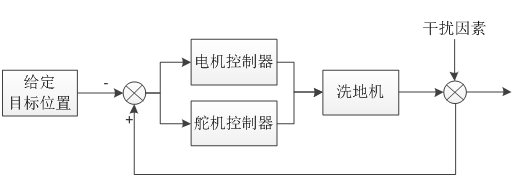
通过控制机器不断调整自身姿态，朝向目标移动，最终可以到达给定目标点，完成运动控制过程。如运动控制原理图所示，机器自身的姿态角为$\theta$，其与目标连线同x轴正半轴的夹角为$\phi$，$\theta$角与$\phi$角的差值为$\delta$。