Python-Matplotlib相关习题及解析

Matplotlib

Exercise 11.1: Plotting a function

Plot the function

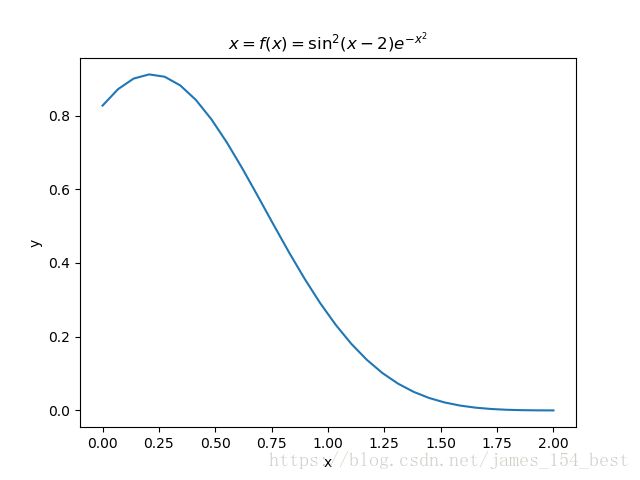
f(x)=sin2(x−2)e−x2 f ( x ) = sin 2 ⁡ ( x − 2 ) e − x 2

over the interval [0,2] [ 0 , 2 ] . Add proper axis labels, a title, etc.

代码

import numpy as np  
import matplotlib.pyplot as plt

x = np.linspace(0,2,30)
y = (np.sin(x-2)**2)*np.exp(-(x**2))
plt.xlabel('x')
plt.ylabel('y')
plt.title('$x=f(x)=\sin^2(x-2)e^{-x^2}$')
plt.plot(x,y)
plt.show()

结果

---

Exercise 11.2: Data

Create a data matrix X X with 20 observations of 10 variables. Generate a vector b b with parameters Then
generate the response vector y=Xb+z y = X b + z where z z is a vector with standard normally distributed variables.
Now (by only using y y and X X ), find an estimator for b b , by solving

b^=argminb∥Xb−y∥2 b ^ = arg ⁡ min b ‖ X b − y ‖ 2

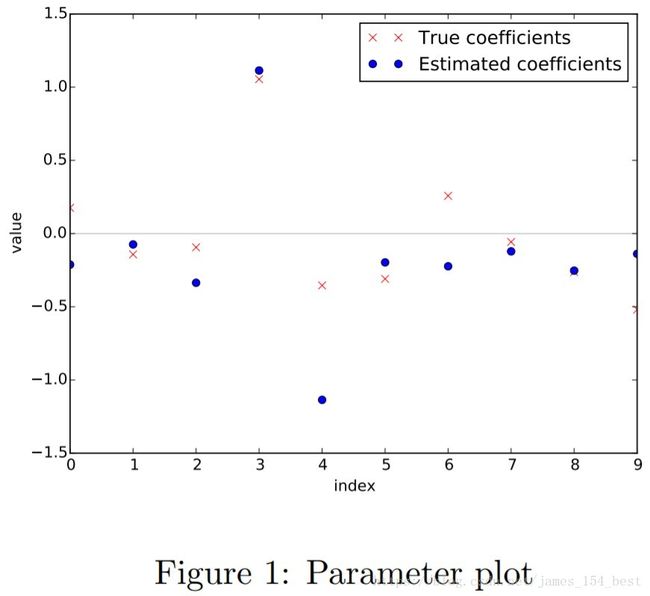
Plot the true parameters b b and estimated parameters b^ b ^ . See Figure 1 for an example plot.

题目分析

• 有一个式子
  x1b1+x2b2+⋯+x10b10=y x 1 b 1 + x 2 b 2 + ⋯ + x 10 b 10 = y
  我们不知道 b=(b1,b2,…,b10) b = ( b 1 , b 2 , … , b 10 ) ，但是我们可以通过20组观察值(observations) xi=(xi1,xi2,…,xi10),i=1,2,…,20 x i = ( x i 1 , x i 2 , … , x i 10 ) , i = 1 , 2 , … , 20 来推测 b b ，且依题意，需要我们使用最小二乘法。
• 但是这道题的意思是，让我们自己先准备一组 b b ，然后再自己编20组 x x ，然后再创建一组符合高斯分布的 z=(z1,z2,…,z10) z = ( z 1 , z 2 , … , z 10 ) ，通过计算
  yi=xi⋅b+zi=xi1b1+xi2b2+⋯+xi10b10+zi y i = x i ⋅ b + z i = x i 1 b 1 + x i 2 b 2 + ⋯ + x i 10 b 10 + z i
  我们就得到了一组 y=(y1,y2,…,y10) y = ( y 1 , y 2 , … , y 10 )
• 现在我们忘记了 b b 和 z z 是多少，但是20组 x x 和 一组 y y 还在，我们想通过它们找回 b b ，即使不能完全一样，差距也不要太大。其实我们可以通过20组 x x 和 一组 y y 用最小二乘法（题目要求）得到一组 b^ b ^ ，且 b^ b ^ 和 b b 的误差比较小
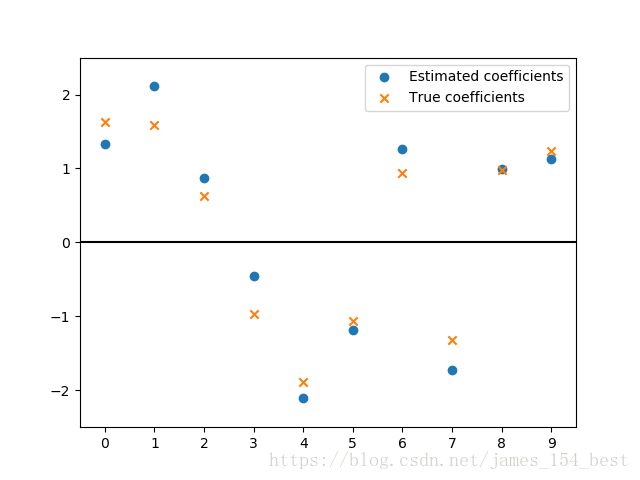
• 画出 b b 和 b^ b ^ ，看看差距有多大

解题步骤

1. 创建 20×10 20 × 10 的矩阵 X X ，代表20组观察值
2. 创建列表 b b ，里面的数可以任意取值，这里我们使用随机整数
3. 创建高斯随机数列表 z z
4. 计算 y y
5. 利用 scipy 的最小二乘函数 leastsq 计算最小二乘解 b^ b ^
6. 对 b b 和 b^ b ^ 画散点图比较

代码

import numpy as np
import matplotlib.pyplot as plt

X = (np.random.random([20,10])-0.5)*2   #生成(20,10)的随机数矩阵，范围在(-1,1)
b = (np.random.random([10])-0.5)*4  #生成(10,)的随机数向量，矩阵相乘会自动变为纵向量
z = np.random.randn(20) #生成(20,)的服从标准正态分布的向量
y = np.dot(X,b)+z   #计算得到(20,)的向量

res = np.linalg.lstsq(X,y)[0]   #计算线性方程组的最小二乘解的基本方法，X和y组成观察值，返回系数向量b

x = range(0,10)
plt.ylim(-2.5,2.5)
plt.xlim(-0.5,9.5)
plt.scatter(x,res,label='Estimated coefficients')
plt.scatter(x,b,marker='x',label=('True coefficients'))
plt.legend()
plt.hlines(0,-0.5,9.5)  #水平分割线
plt.xticks(range(0,10))
plt.plot()

结果

---

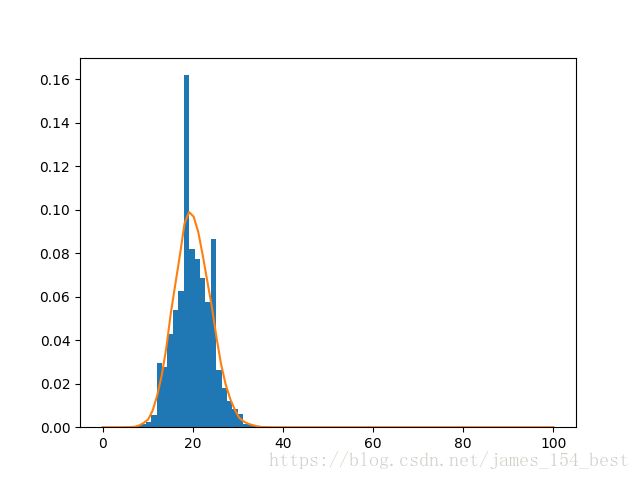
Exercise 11.3: Histogram and density estimation

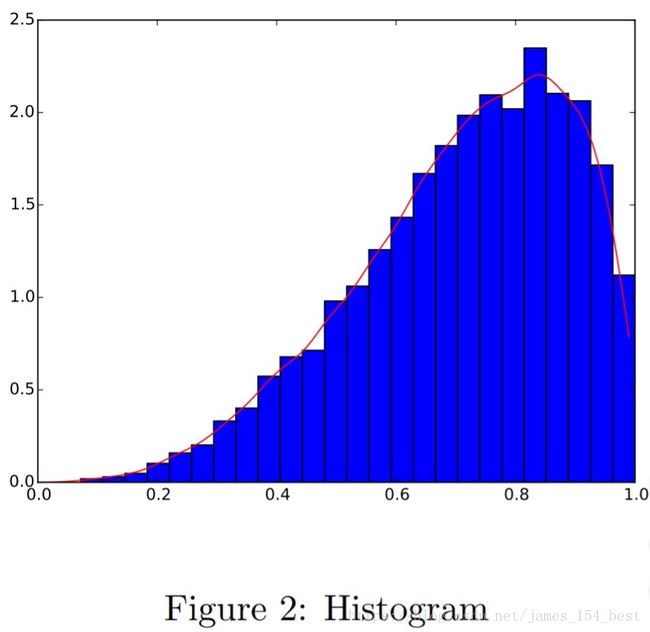
Generate a vector z z of 10000 observations from your favorite exotic distribution. Then make a plot that
shows a histogram of z z (with 25 bins), along with an estimate for the density, using a Gaussian kernel
density estimator (see scipy.stats). See Figure 2 for an example plot.

代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

data = np.random.binomial(100,0.2,10000)
x = np.linspace(0,100,100)

kernel = stats.gaussian_kde(data)
kde = kernel.evaluate(x)

plt.hist(kernel.dataset[0],normed='True',bins=25)
plt.plot(x,kde)
plt.show()

结果