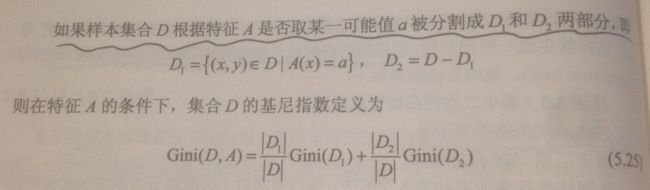机器学习----笔记之决策树(3)
决策树(decision tree)(由于水平有限,在这里暂时只介绍分类算法)
1.算法思路:根据已有数据集,通过一定的评估条件构建一棵树形结构--决策树。决策树由节点和有向边组成,其中叶节点为类别标签,非叶节点为评估条件。分类时,用一条未知类别的数据与树形结构的节点进行匹配查询,最终找到唯一叶节点,该叶节点的类别标签即该未知类别数据的类别。
2.常见的决策树算法:ID3、C4.5、CART算法等,下文将逐步展开介绍。
3.决策树模型构建的三部曲:特征选择、决策树生成、决策树剪枝。
3.1特征的选择:
算法ID3的特征选择准则是信息增益,C4.5在ID3的基础上改进使用信息增益比,CART分类算法的特征选择准则是基尼指数,CART回归算法的特征选择准则是平方误差最小化。
3.1.1信息增益
了解信息增益需要首先了解熵和条件熵的概念。特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即 g(D,A)=H(D)-H(D|A)。信息增益g(D,A)代表在特征A给定值之前数据集D进行分类的不确定性与特征A给定值之后数据集D进行分类的不确定性之差,熵越大不确定性越大。也就是说,g(D,A)表示当特征A给定值之后,对于数据集D分类的不确定性减小的程度。(个人理解为当特征A给定值后,数据集D中有些数据已经确定类别了,或者根据特征A给定的值能将数据集D大致分类了。)
(一般地,熵H(Y)与条件熵H(Y|X)之差称为互信息。决策树学习中的信息增益等价于训练数据集中类和特征的互信息。)
在ID3算法中,根据信息增益选择特征的方法是:对训练数据集D,计算各个特征的信息增益,选择信息增益最大的特征。
3.1.2信息增益比
以信息增益作为划分训练数据集的特征,存在偏向于选择取值较多的特征的问题。信息增益比可以对这一问题进行矫正,C4.5就是通过比较各特征的信息增益比替代信息增益来选取特征的,同样选取信息增益比最大的特征。
信息增益比:特征A对训练数据集D的信息增益比gr(D,A)定义为其信息增益g(D,A)与训练数据集D关于特征A的值的熵Ha(D)之比,即gr(D,A)=g(D,A)/Ha(D)。其中Ha(D)是按照特征A的取值将数据集D划分为Di,(i=1,2,…,m,其中m表示特征A的取值个数),P(Di)=|Di|/|D|,即数据子集Di中数据个数与数据集D中数据个数的比值。
3.1.3基尼指数
基尼指数Gini(D)表示数据集D的不确定性,基尼指数Gini(D,A)表示经过A=a分割后数据集D的不确定性。基尼指数值越大,样本集合的不确定性也就越大,这一点与熵相似。具体计算见下图:
CART决策树是二叉树,节点中包括选择的特征和该特征的取值,训练集D中各数据对应特征的值比节点值小的数据放在节点的左孩子,对应特征的值比该节点值大的数据放在节点的右孩子。因此在CART算法中,特征的选择包括选择特征和选择特征的取值(切分点)两部分。CART分类中,计算所有特征A以及他们所有可能的切分点a的基尼指数,选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点。
3.1.4平方误差最小化
在CART构建回归树的时候,以平方误差最小化准则选取特征。(这里先略过,日后再补充。)
3.2决策树生成(书上的算法个人觉得有错误或难以理解,下面给出个人理解的算法流程)
3.2.1 ID3决策树生成算法
输入:训练数据集D,特征集A,阈值ε;
输出:决策树T
1)若D中所有实例属于同一类C,则T为单节点树,并将类C作为该节点的类标记,返回T;
2)若A=∅,则T为单节点树,并将D中实例数最大的类C作为该节点的类标记,返回T;
3)否则,计算A中各特征对D的信息增益,选择A中信息增益最大的特征Ai;
4)如果Ai的信息增益小于阈值ε,则T为单节点树,并将D中实例数最大的类C作为该节点的类标记,返回T;
5)否则,以特征标签Ai为T的根节点,特征Ai中各个取值aj下包含的非空数据集Dj为训练数据集,A-Ai为特征集,ε为阈值,递归调用该生成算法生成m个子树Tc(其中m表示特征Ai的取值个数);
6)返回T。
3.2.2 C4.5决策树生成算法
与ID3类似,不同之处就是在特征选取时用信息增益比代替了信息增益作为最优特征选取的标准。这里不再叙述。
3.2.3 CART决策树生成算法(分类)
输入:数据集D、停止条件
输出:CART决策树
根据训练数据集,从根节点开始,递归地对每个节点进行以下操作,构建二叉决策树。
1)设节点的训练数据集D,计算现有特征对该数据集地基尼指数Gini(D),对每个特征A,以及可能取的每个值a,根据样本点对A=a的测试为“是”和“否”将D分割成D1和D2两部分,计算A=a时的基尼指数Gini(D,A)。
2)在所有可能的特征A以及他们所有可能的切分点a中,选择基尼指数最小的特征及其对应的切分点作为最优特征和最优切分点,作为该子树的根节点。根据最优特征和最优切分点从根节点生成两个子节点,将训练数据集按照特征和切分点分配到两个子节点中。
3)对两个子节点递归调用1),2),直到满足停止条件。
4)返回生成的CART决策树。
3.3决策树剪枝
决策树生成时过多考虑如何提高训练数据地正确分类,从而构建了过于复杂的决策树。这种决策树往往对训练数据分类准确,但是对未知的测试数据分类准确度下降,即出现过拟合。解决过拟合的办法就是简化决策树。
对已生成的决策树进行简化的过程称为剪枝。具体的,就是在已生成的树中剪掉部分子树或叶节点,使子树或叶节点的父节点变成新的叶节点,从而简化分类树模型。
决策树剪枝往往通过极小化决策树整体的损失函数(loss function)或代价函数(cost function)来实现。(具体实现步骤以后再补充)
4.python代码实现
4.1 ID3和C4.5的Python实现代码
首先添加引用包
from math import log
import operator1)计算给定数据集dataSet的香浓熵
def calcShannonEnt(dataSet):
'''
计算给定数据集的香浓熵
:param dataSet: 给定数据集
:return: 数据集的熵
'''
numEntries=len(dataSet)#训练集的数据量
labelCounts={}#类别字典(类别的名称为键,该类别的个数为值)
for featVec in dataSet:#遍历数据集,实例化类别字典
currentLabel=featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1
shannonEnt=0.0
for key in labelCounts:
prob=float(labelCounts[key])/numEntries#P(Di)
shannonEnt-=prob*log(prob,2)
return shannonEnt2)按照给定特征序号和特征的值划分数据集
def splitDataSet(dataSet,axis,value):
'''
按照给定特征给定值划分数据集
:param dataSet: 数据集
:param axis: 特征所在数据集的列号
:param value: 特征的值
:return:特征axis的值等于value并去除特征axis列的数据子集
'''
retDataSet=[]
for featVec in dataSet:
if featVec[axis]==value:
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSetdef majorityCnt(classList):
'''
进行多数表决,返回实例数最多的类别标签
:param classList: 类别标签列表
:return: 多数表决后的类别标签
'''
classCount={}
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount[vote]+=1
sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]4.1)采用ID3的最大信息增益,选择最优特征
def chooseBestFeatureToSplitForID3(dataSet):
'''
获得最优特征来划分数据集
:param dataSet: 给定数据集
:return: 最优特征列序号(信息增益最大的特征)
'''
numFeatures=len(dataSet[0])-1#特征个数
baseEntropy=calcShannonEnt(dataSet)#数据集dataSet的熵
bestInfoGain=0.0;bestFeature=-1#最优信息增益和最优特征
for i in range(numFeatures):#对于每一个特征列
featList=[example[i] for example in dataSet]#获取该特征列的值
uniqueVals=set(featList)#获得该特征的所有唯一特征值
newEntroy=0.0#i特征的信息熵
for value in uniqueVals:
subDataSet=splitDataSet(dataSet,i,value)#按照i特征的value唯一特征值--拆分数据集
prob=len(subDataSet)/float(len(dataSet))#新数据集占总数据的比例
newEntroy+=prob*calcShannonEnt(subDataSet)#给定特征i的数据集dataSet的条件熵
infoGain=baseEntropy-newEntroy#按照i特征划分的信息增益(数据集dataSet的熵-给定特征i的数据集dataSet的条件熵)
if(infoGain>bestInfoGain):
bestInfoGain=infoGain
bestFeature=i
return bestFeature4.2)采用C4.5的最大信息增益比,选择最优特征
def chooseBestFeatureToSplitForC45(dataSet):
'''
获得最优特征来划分数据集
:param dataSet: 给定数据集
:return: 最优特征序号(信息增益比最大的特征)
'''
numFeatures = len(dataSet[0]) - 1 # 特征个数
baseEntropy = calcShannonEnt(dataSet) # 数据集dataSet的熵
bestInfoGainRatio = 0.0;
bestFeature = -1 # 最优信息增益和最优特征
for i in range(numFeatures): # 对于每一个特征列
featList = [example[i] for example in dataSet] # 获取该特征列的值
uniqueVals = set(featList) # 获得该特征的所有唯一特征值
newEntroy = 0.0 # 给定特征i的数据集dataSet的条件熵
ibaseEntroy=0.0#数据集dataSet关于特征i的值的熵(数据集dataSet按照特征i的值划分的各子集的熵*子集占dataSet的比例之和)
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value) # 按照i特征的value唯一特征值--拆分数据集
prob = len(subDataSet) / float(len(dataSet)) # 新数据集占总数据的比例
newEntroy += prob * calcShannonEnt(subDataSet)
ibaseEntroy-=prob*log(prob,2)
infoGainRatio = (baseEntropy - newEntroy)/ibaseEntroy # 按照i特征划分的信息增益比
if (infoGainRatio > bestInfoGainRatio):
bestInfoGainRatio = infoGainRatio
bestFeature = i
return bestFeature5)创建决策树
def createTree(dataSet,labels):
#dataset包括特征和类别
#labels表示每一列特征的名称
labels=labels[:]#深拷贝,不然删除后面del(labels[bestFeat])后原始标签少一个。
classList=[example[-1] for example in dataSet]#类标签列表
if classList.count(classList[0])==len(classList):#如果所有类都一样
return classList[0]#返回类别标签
if len(dataSet[0])==1:#如果训练集只有类别标签,没有任何特征列
return majorityCnt(classList)#返回实例数最多的类别标签
bestFeat=chooseBestFeatureToSplitForID3(dataSet)#最优特征列的序号
bestFeatLabel=labels[bestFeat]#最优特征名称
myTree={bestFeatLabel:{}}#以bestFeatLabel为根节点的树
del(labels[bestFeat])#在特征列表中删除已选做最优特征的特征
featValues=[example[bestFeat] for example in dataSet]#最优特征的所有取值
uniqueVals=set(featValues)#最优特征集合(集合各特征值唯一)
for value in uniqueVals:#对于集合中每个特征值
subLabels=labels[:]#深拷贝特征列表,防止修改labels的值。
# 递归调用,并将返回的树放在最优特征对应的各个value分支下
myTree[bestFeatLabel][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
return myTree6)使用决策树进行分类
def classify(inputTree,featLabels,testVec):
firstStr=inputTree.keys()[0]
secondDict=inputTree[firstStr]
featIndex=featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex]==key:
if type(secondDict[key]).__name__=='dict':
classLabel=classify(secondDict[key],featLabels,testVec)
else:
classLabel=secondDict[key]
return classLabeldef storeTree(inputTree,filename):
import pickle
fw=open(filename,'w')
pickle.dump(inputTree,fw)
fw.close()
def grabTree(filename):
import pickle
fr=open(filename)
return pickle.load(fr)#创建简单的数据集
def createDataSet():
dataSet=[[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels=['no surfacing','flippers']
return dataSet,labels
#测试分类结果
myDat,labels=createDataSet()
myTree=createTree(myDat,labels)
print classify(myTree,labels,[1,0])
print classify(myTree,labels,[1,1])
'''
storeTree(myTree,'classifierStorage.txt')
print grabTree('classifierStorage.txt')
'''4.2 CART决策树代码实现:
CART算法的思想和ID3以及C4.5是不太一样的,前面已经提到过,CART生成的是二叉树,下面给出CART生成二叉决策树的python代码:
1)计算给定数据集的吉尼指数
def calcGini(dataSet):
'''
计算数据集的吉尼指数
:param dataSet:
:return: 数据集dataSet的吉尼指数
'''
numEntries=len(dataSet)
labelCounts={}
#给所有可能分类创建字典
for featVec in dataSet:
currentLabel=featVec[-1]
if currentLabel not in labelCounts:
labelCounts[currentLabel]=0
labelCounts[currentLabel]+=1
#计算吉尼指数
Gini=1.0
for key in labelCounts.keys():
prob=float(labelCounts[key])/numEntries
Gini-=prob**2
return Gini2)计算给定数据集,给定特征列序号,以及给定划分特征值的吉尼指数,也就是数据集D在特征A=a值时候的吉尼指数
def calcConditionGini(dataSet,axis,value):
'''
计算数据集dataSet关于特征序号为axis,特征值为value的条件吉尼指数
:param dataSet:
:param axis:
:param value:
:return:
'''
dataSetEqual,dataSetNotEqual=splitDataSet(dataSet,axis,value)
conditionGini=(len(dataSetEqual)*calcGini(dataSetEqual)+len(dataSetNotEqual)*calcGini(dataSetNotEqual))/len(dataSet)
return conditionGini3)根据特征和特征值切分数据集
def splitDataSet(dataSet,axis,value):
'''
对离散数据:
根据特征序号axis和特征值划分数据集
:param dataSet:
:param axis: 特征序号
:param value: 特征值
:return: 特征序号axis中的特征值等于value的数据集和剩余数据集
'''
dataSetEqual=[];dataSetNotEqual=[]
for featVec in dataSet:
if featVec[axis]==value:#如果特征值等于value则划分到左边,并去除该特征
reducedFeatVec=featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
dataSetEqual.append(reducedFeatVec)
else:#如果特征值不等于value,则划分到右边
dataSetNotEqual.append(featVec)
return dataSetEqual,dataSetNotEqual4)选择吉尼指数最小的最优特征和最优特征值对
def chooseBestFeatureAndValue(dataSet,labels):
'''
获得最优特征和最优特征值
:param dataSet:
:param labels:最优特征标签列表
:return: 返回最优特征标签和最优值
'''
numFeatures=len(dataSet[0])-1
bestGini=100000.0
bestFeature=-1
bestValue=0.0
for i in range(numFeatures):#对于每一个特征
featList=[example[i] for example in dataSet]
featList=set(featList)#获取该特征的唯一特征值集合
for value in featList:#对于特征i下的每个特征值计算条件吉尼指数
newGiniContiation=calcConditionGini(dataSet,i,value)
if newGiniContiation5)多数表决函数
def majorityCnt(classList):
'''
多数表决
:param classList:
:return:类别标签
'''
classCount={}
for vote in classList:
if vote not in classCount.keys():
classCount[vote]=0
classCount+=1
return sorted(classCount.items(),lambda item:item[1])[0][0]6)创建二叉决策树(CART决策树)
def createTree(dataSet,labels):
classList=[example[-1] for example in dataSet]#类别标签列表
if classList.count(classList[0])==len(classList):#如果都是同一类
return (classList[0],None)#返回该类别和空值
if len(dataSet[0])==1:#如果没有特征可选择了
return (majorityCnt(classList),None)#返回多数表决的类别标签和空值
#选择最优特征和最优值作为非叶子节点
bestFeat,bestValue=chooseBestFeatureAndValue(dataSet,labels)
myTree={(bestFeat,bestValue):{}}
dataSetEqual,dataSetNotEqual=splitDataSet(dataSet,labels.index(bestFeat),bestValue)
#递归调用createTree函数
leftLabels=[label for label in labels if label!=bestFeat]
leftTree=createTree(dataSetEqual,leftLabels)
rightTree=createTree(dataSetNotEqual,labels)
myTree[(bestFeat,bestValue)]['left']=leftTree
myTree[(bestFeat,bestValue)]['right']=rightTree
return myTree7)测试,为了显示CART决策树与ID3和C4.5的不同,这里将上边使用的数据集稍作了修改。
def createDataSet():
dataSet=[[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[2,1,'no'],
[0,1,'no']]
labels=['no surfacing','flippers']
return dataSet,labelsdata,labels=createDataSet()
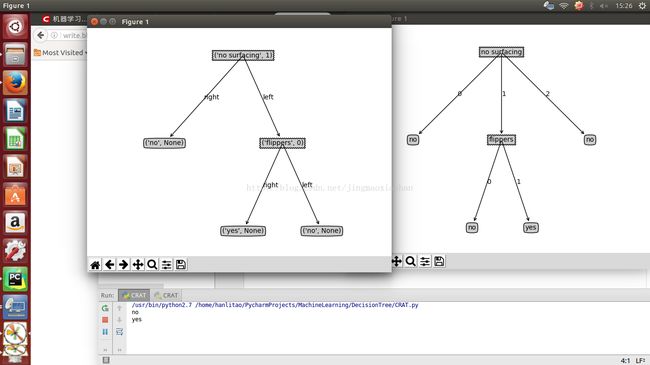
myTree = createTree(data, labels)至此,CART分类决策树已经生成了。以下是利用第二个数据集,分别采用CART和ID3生成的决策树。
8)最后再添加针对上边CART树结构可用的分类函数
def classify(inputTree,featLabels,testVec):
'''
进行分类
:param inputTree:
:param featLabels:
:param testVec:
:return: 分类结果
'''
if type(inputTree).__name__=='tuple':#如果是叶节点,返回类别标签
return inputTree[0]
else:
firstNode=inputTree.keys()[0]
featLabel=firstNode[0]
featIndex=featLabels.index(featLabel)
if firstNode[1]==testVec[featIndex]:#如果值相同,进入左子树
newFeatLabel=[label for label in featLabels if label!=featLabel]
newTestVec=[testVec[i] for i in range(len(testVec)) if i!=featIndex]
return classify(inputTree[firstNode]['left'],newFeatLabel,newTestVec)
else:#否则进入右子树
return classify(inputTree[firstNode]['right'],featLabels,testVec) 4.3.树的剪枝
5.思考:
敬请期待
(其他内容后续再修改补充)