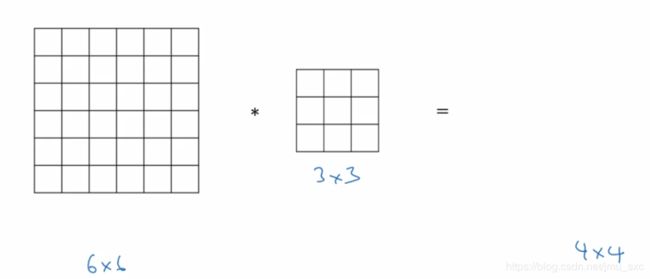卷积神经网络(CNN)
卷积神经网络(CNN)
文章目录
- 卷积神经网络(CNN)
- 1.什么是CNN
- 2.CNN组成架构
- 3.工作原理
- 卷积
- 参数
- 池化
- 卷积网络事例(conv-pool-conv-pool-fc-fc-fc-softmax)
- 4.CNN优势
- 5.应用
- 6.总结
1.什么是CNN
CNN是深度学习的代表算法之一,它是一类包含卷积计算具有深度的前馈神经网络,结构跟普通的神经网络相似,都是由可学习的权重和偏置的神经元组成。在计算机视觉等邻域中网络的输入往往是很大的,需要读取整幅图像作为神经网络模型的输入(即全连接的方式),当图像的尺寸越大时,其连接的参数将变得很多,从而导致计算量非常大。如下图:
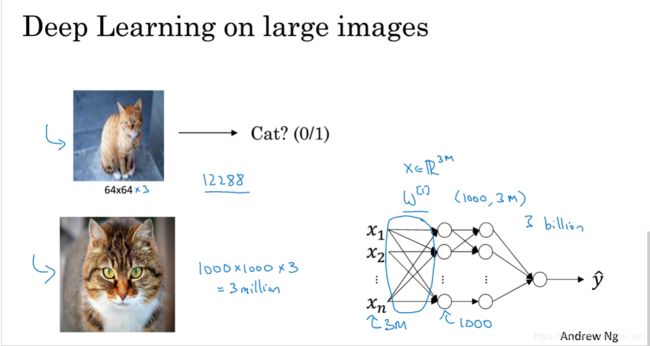
在传统的神经网络的计算下,1000×1000×3的图像的输入,光第一层的权重就需要(1000,3m)个。这样的计算代价是巨大的。CNN解决的这个问题,卷积运算使得无论输入的维度是多少,网络的参数都是固定的,而且参数量远少于传统的算法。
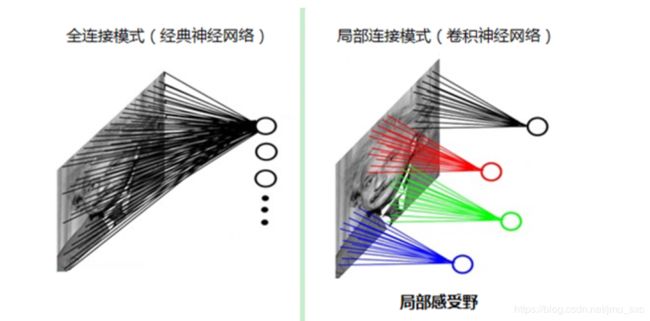
而我们人类对外界的认知一般是从局部到全局,先对局部有感知的认识,再逐步对全体有认知,这是人类的认识模式。在图像中的空间联系也是类似,局部范围内的像素之间联系较为紧密,而距离较远的像素则相关性较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。这种模式就是卷积神经网络中降低参数数目的重要神器:局部感受野
2.CNN组成架构
-
卷积层
卷积神经网路中每层卷积层由若干卷积单元组成,每个卷积单元的参数都是通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征,第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网络能从低级特征中迭代提取更复杂的特征
-
激活
这一层神经的激活函数(Activation function)使用线性整流(Rectified Linear Units, ReLU)。
-
池化层
通常在卷积层之后会得到维度很大的特征,将特征切成几个区域,取其最大值或平均值,得到新的、维度较小的特征
-
全连接层
把所有局部特征结合变成全局特征,用来计算最后每一类的得分
3.工作原理
卷积
卷积运算过程是什么样的?
卷积操作总的来说就是对图像上的每个像素中提取某些特征,滤波器要扫过图像的每个像素,从左到右,从上到下。图像上被滤波器访问的像素点与滤波器的对应的权重进行点积再求和取平均值,该值作为该位置的特征。
具体的计算过程可以参考吴恩达的课程
几种不同的卷积运算
- 二维的图像输入,即灰度图在一个3×3的滤波器的卷积运算下,步长为1,输出的图像大小为4×4
- 三维的图像输入,即RGB图在一个3×3的滤波器的卷积运算下,步长为1,输出的图像大小依然为4×4
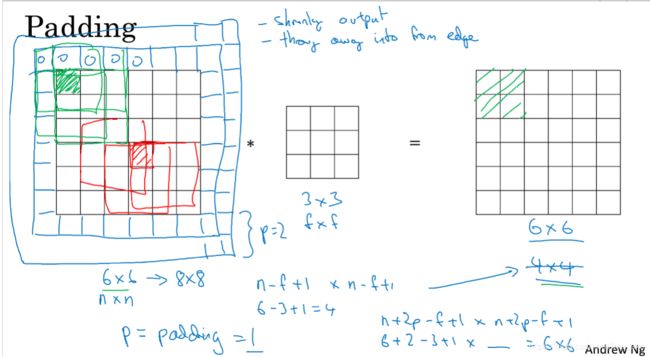
输出图像变小与输出图像大小不变(padding操作):
为了防止卷积操作带来的维度下降,padding操作在图像的边缘填充像素点,使得原图像的边缘的像素点能被多次使用,就像图形中心的像素值会参与多次卷积运算。选择合适的填充个数,会使得图像大小在卷积后不变。
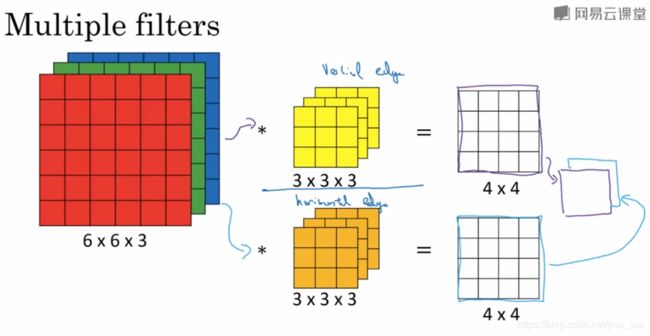
滤波器的数量影响输出的维度:
在熟悉卷积操作后,我们知道,无论在灰度图或者RGB图像中,即图像的通道数是1或者3或者其他通道数,滤波器的通道数对应输入图像的通道数,但在一个滤波器的卷积运算的结果中,输出的通道数还是为1。也就是说滤波器的个数多少,输出的特征图的通道数就是多少。换一种理解,一个滤波器代表提取一种特征,无论输入的图像的通道数是多少输出的特征,输出的特征的维度跟滤波器的维度一样。
参数
输出特征图维度计算:W=(n+2p-f) / s + 1,通道数就是滤波器的个数
参数个数计算:[f × f + b(一个) ] × 滤波器个数
单层卷积神经网络的计算过程
1.图像作为输入,RGB三通道,使用若干个滤波器大小为3×3×3(最后的3表示3个通道),滤波器上的值为权重,进行卷积操作后得到的结果(结果为二维的值)后再通过numpy广播对每个二维矩阵的值加上偏置(常数),然后经过一个激活函数(RELU)后作为特征图的一个通道
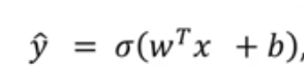
X的值为图像的像素值(6×6×3),W为权重,一个W为一个滤波器上的值。矩阵W乘上X后加上偏置后使用激活函数后作为该层卷积神经网络的输出的一个通道,一个特征。几个滤波器得到的特征结果叠加起来就是该层网络的输出(不同特征的集合4×4×2)。该层的输出作为下一层的输入。
简单卷积网络示例
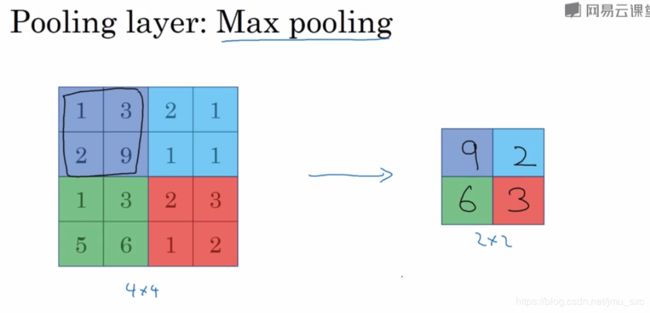
池化
对每个通道单独计算最大池化,(不像卷积中每个通道相应的位置要相加)输入有几个通道输出就有几个。上图中f为2,s为2,输出为4×4,最后输出为(4+0-2 )/ 2 +1= 2。输出为2×2。如果输入有n个通道,最后输出也有n个通道。输出的值为f×f中取最大的像素值。
一般超参数设置为:f=2,s=2;f=3,s=2;其他参数看池化的类型。超参数padding一般不用。
池化的作用:缩减模型的大小,提高计算速度,同时提高所提取的特征的鲁棒性。
直观理解:如果滤波器提取到特征,那么就保留特征的最大值,如果没有提取到,可能该地方就没有该特征,那么该最大值也会很小。
参数特点:有参数,但并没有参数需要学习,梯度下降没什么可学的,一旦f和s确定就是一个固定的运算,梯度下降无需改变任何值。
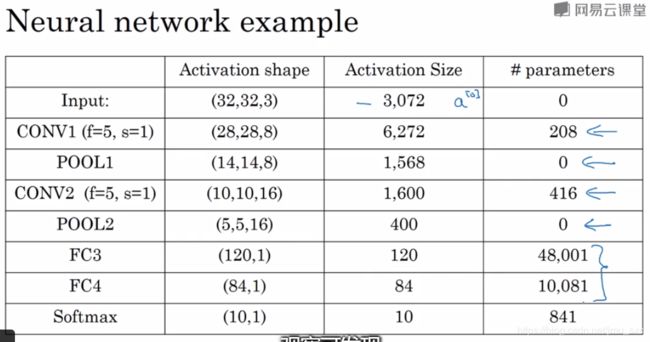
卷积网络事例(conv-pool-conv-pool-fc-fc-fc-softmax)
4.CNN优势
和只用全卷积神经网路相比,CNN的两个优势是参数共享和稀疏连接。
CNN平移不变性
CNN参数少的原因:
参数共享:一个滤波可以对输入图像的多个位置使用。
更准确的说它允许在整个输入值的多个位置使用特征检测器
稀疏连接:输出结果的每一个单元之和输入图像的n×n个单元(滤波的大小)有关。即下一层中的每个激活只依赖于前一层的少量激活
1.Training set x(1),y(1)…x(m),y(m))
2.选择一个卷积神经网络(卷积,池化,全连接)有很多参数权重W和偏置b,随机初始化参数
cost等于神经网络对整个训练集的预测的损失的总和再除以m
训练神经网络:使用梯度下降算法来优化神经网络的所有参数以减小Cost的值,直到满足一个条件
5.应用
计算机视觉领域
LeNet
AlexNet
ResNet
…
自然语音处理领域
6.总结
通过学习吴恩达卷积神经网络课程,对CNN有了更加深入的了解。CNN的出现解决了传统的神经网络在处理图像等大输入中网络参数量大,计算代价大的问题。特别在计算机视觉领域,卷积神经网络的计算过程遵循从图像局部到全局的理解过程。CNN局部感受野概念中每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。
CNN的计算过程:图像在各种卷积层中的各个卷积核的卷积下,提取特征,生成各个层的特征图。每一层的卷积的输入是上一层卷积生成的特征图。在每个卷积层中,特征图会进行卷积运算后经过激活函数生成合适的特征图,在每一层中,卷积计算后一般都会跟上一个采样层(或者说池化层),这一层的为了减少运算量,实验表明,加上这一层会提高运算结果。我们一般把卷积层和池化层作为CNN中的一层(layer)。
在CNN最后,我们会将最后一层的特征图用来进行分类和回归。这个特征图我们会使用1X1的卷积,将它变成一个1×n维的向量,我们称为全连接层,n个神经元最为n个特征,全连接层用来作为对n个特征的组合的功能。