第七章 支持向量机
第七章 支持向量机
基本梳理
- 参考链接:https://zhuanlan.zhihu.com/p/36332083
-
二分类模型,间隔最大化的分类器
- 训练数据线性
- 可分
- 硬间隔支持向量机
- 近似可分
- 软间隔支持向量机
- 不可分
- 非线性支持向量机
- 可分
- 训练数据线性
-
感知机特殊情况
-
线性支持向量机
-
线性支持向量机
- 假设函数
- y ^ = sign ( w T x + b ) \hat { y } = \operatorname { sign } \left( w ^ { T } x + b \right) y^=sign(wTx+b)
- 其中 sign ( x ) = { − 1 x < 0 1 x ≥ 0 \operatorname { sign } ( x ) = \left\{ \begin{array} { l l } { - 1 } & { x < 0 } \\ { 1 } & { x \geq 0 } \end{array} \right. sign(x)={−11x<0x≥0
- y ^ = sign ( w T x + b ) \hat { y } = \operatorname { sign } \left( w ^ { T } x + b \right) y^=sign(wTx+b)
- 代价函数
- J ( θ ) = max { 0 , 1 − y y ^ } J ( \theta ) = \max \{ 0,1 - y \hat { y } \} J(θ)=max{0,1−yy^}
- 优化算法
- 凸优化
- SMO算法
- 假设函数
-
线性支持向量机的公式推导
-
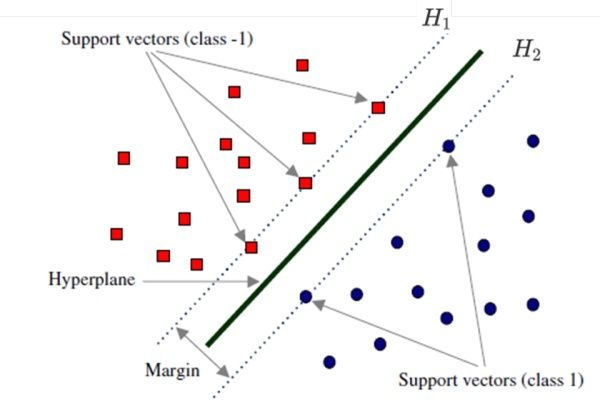
支持向量
-
函数间隔与几何间隔
- 几何间隔 γ = y ( w T x + b ) ∥ w ∥ 2 \gamma = \frac { y \left( w ^ { T } x + b \right) } { \| w \| _ { 2 } } γ=∥w∥2y(wTx+b)
- 函数间隔 γ ′ = y ( w T x + b ) \gamma ^ { \prime } = y \left( w ^ { T } x + b \right) γ′=y(wTx+b)
- 几何间隔可以理解为对函数间隔做了归一化的处理
-
怎样定义最大间隔
- max 2 ∥ w ∥ 2 \max \frac { 2 } { \| w \| _ { 2 } } max∥w∥22 s.t y i ( w T x i + b ) ≥ 1 ( i = 1 , 2 , … m ) y _ { i } \left( w ^ { T } x _ { i } + b \right) \geq 1 ( i = 1,2 , \ldots m ) yi(wTxi+b)≥1(i=1,2,…m)
- 等价于
- min 1 2 ∥ w ∥ 2 2 \min \frac { 1 } { 2 } \| w \| _ { 2 } ^ { 2 } \quad min21∥w∥22 s.t y i ( w T x i + b ) ≥ 1 ( i = 1 , 2 , … m ) y _ { i } \left( w ^ { T } x _ { i } + b \right) \geq 1 ( i = 1,2 , \dots m ) yi(wTxi+b)≥1(i=1,2,…m)
-
求解最大间隔
- 转化为拉格朗日函数
- L ( w , b , α ) = 1 2 ∥ w ∥ 2 2 − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 ] L ( w , b , \alpha ) = \frac { 1 } { 2 } \| w \| _ { 2 } ^ { 2 } - \sum _ { i = 1 } ^ { m } \alpha _ { i } \left[ y _ { i } \left( w ^ { T } x _ { i } + b \right) - 1 \right] \quad L(w,b,α)=21∥w∥22−∑i=1mαi[yi(wTxi+b)−1] s. t$ \alpha _ { i } \geq 0$
- 转化为对偶问题
- 简化对偶问题
- SMO算法求解α
- 根据α求解出w 和 b
- 转化为拉格朗日函数
-
线性可分SVM的算法过程
-
-
代码小练习
分离超平面: w T x + b = 0 w^Tx+b=0 wTx+b=0
点到直线距离: r = ∣ w T x + b ∣ ∣ ∣ w ∣ ∣ 2 r=\frac{|w^Tx+b|}{||w||_2} r=∣∣w∣∣2∣wTx+b∣
∣ ∣ w ∣ ∣ 2 ||w||_2 ∣∣w∣∣2为2-范数: ∣ ∣ w ∣ ∣ 2 = ∑ i = 1 m w i 2 2 ||w||_2=\sqrt[2]{\sum^m_{i=1}w_i^2} ∣∣w∣∣2=2∑i=1mwi2
直线为超平面,样本可表示为:
w T x + b ≥ + 1 w^Tx+b\ \geq+1 wTx+b ≥+1
w T x + b ≤ + 1 w^Tx+b\ \leq+1 wTx+b ≤+1
margin:
函数间隔: l a b e l ( w T x + b ) o r y i ( w T x + b ) label(w^Tx+b)\ or\ y_i(w^Tx+b) label(wTx+b) or yi(wTx+b)
几何间隔: r = l a b e l ( w T x + b ) ∣ ∣ w ∣ ∣ 2 r=\frac{label(w^Tx+b)}{||w||_2} r=∣∣w∣∣2label(wTx+b),当数据被正确分类时,几何间隔就是点到超平面的距离
为了求几何间隔最大,SVM基本问题可以转化为求解:( r ∗ ∣ ∣ w ∣ ∣ \frac{r^*}{||w||} ∣∣w∣∣r∗为几何间隔,( r ∗ {r^*} r∗为函数间隔)
max r ∗ ∣ ∣ w ∣ ∣ \max\ \frac{r^*}{||w||} max ∣∣w∣∣r∗
( s u b j e c t t o ) y i ( w T x i + b ) ≥ r ∗ , i = 1 , 2 , . . , m (subject\ to)\ y_i({w^T}x_i+{b})\geq {r^*},\ i=1,2,..,m (subject to) yi(wTxi+b)≥r∗, i=1,2,..,m
分类点几何间隔最大,同时被正确分类。但这个方程并非凸函数求解,所以要先①将方程转化为凸函数,②用拉格朗日乘子法和KKT条件求解对偶问题。
①转化为凸函数:
先令 r ∗ = 1 {r^*}=1 r∗=1,方便计算(参照衡量,不影响评价结果)
max 1 ∣ ∣ w ∣ ∣ \max\ \frac{1}{||w||} max ∣∣w∣∣1
s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , . . , m s.t.\ y_i({w^T}x_i+{b})\geq {1},\ i=1,2,..,m s.t. yi(wTxi+b)≥1, i=1,2,..,m
再将 max 1 ∣ ∣ w ∣ ∣ \max\ \frac{1}{||w||} max ∣∣w∣∣1转化成 min 1 2 ∣ ∣ w ∣ ∣ 2 \min\ \frac{1}{2}||w||^2 min 21∣∣w∣∣2求解凸函数,1/2是为了求导之后方便计算。
min 1 2 ∣ ∣ w ∣ ∣ 2 \min\ \frac{1}{2}||w||^2 min 21∣∣w∣∣2
s . t . y i ( w T x i + b ) ≥ 1 , i = 1 , 2 , . . , m s.t.\ y_i(w^Tx_i+b)\geq 1,\ i=1,2,..,m s.t. yi(wTxi+b)≥1, i=1,2,..,m
②用拉格朗日乘子法和KKT条件求解最优值:
min 1 2 ∣ ∣ w ∣ ∣ 2 \min\ \frac{1}{2}||w||^2 min 21∣∣w∣∣2
s . t . − y i ( w T x i + b ) + 1 ≤ 0 , i = 1 , 2 , . . , m s.t.\ -y_i(w^Tx_i+b)+1\leq 0,\ i=1,2,..,m s.t. −yi(wTxi+b)+1≤0, i=1,2,..,m
整合成:
L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( − y i ( w T x i + b ) + 1 ) L(w, b, \alpha) = \frac{1}{2}||w||^2+\sum^m_{i=1}\alpha_i(-y_i(w^Tx_i+b)+1) L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(−yi(wTxi+b)+1)
推导: min f ( x ) = min max L ( w , b , α ) ≥ max min L ( w , b , α ) \min\ f(x)=\min \max\ L(w, b, \alpha)\geq \max \min\ L(w, b, \alpha) min f(x)=minmax L(w,b,α)≥maxmin L(w,b,α)
根据KKT条件:
∂ ∂ w L ( w , b , α ) = w − ∑ α i y i x i = 0 , w = ∑ α i y i x i \frac{\partial }{\partial w}L(w, b, \alpha)=w-\sum\alpha_iy_ix_i=0,\ w=\sum\alpha_iy_ix_i ∂w∂L(w,b,α)=w−∑αiyixi=0, w=∑αiyixi
∂ ∂ b L ( w , b , α ) = ∑ α i y i = 0 \frac{\partial }{\partial b}L(w, b, \alpha)=\sum\alpha_iy_i=0 ∂b∂L(w,b,α)=∑αiyi=0
带入$ L(w, b, \alpha)$
min L ( w , b , α ) = 1 2 ∣ ∣ w ∣ ∣ 2 + ∑ i = 1 m α i ( − y i ( w T x i + b ) + 1 ) \min\ L(w, b, \alpha)=\frac{1}{2}||w||^2+\sum^m_{i=1}\alpha_i(-y_i(w^Tx_i+b)+1) min L(w,b,α)=21∣∣w∣∣2+∑i=1mαi(−yi(wTxi+b)+1)
= 1 2 w T w − ∑ i = 1 m α i y i w T x i − b ∑ i = 1 m α i y i + ∑ i = 1 m α i \qquad\qquad\qquad=\frac{1}{2}w^Tw-\sum^m_{i=1}\alpha_iy_iw^Tx_i-b\sum^m_{i=1}\alpha_iy_i+\sum^m_{i=1}\alpha_i =21wTw−∑i=1mαiyiwTxi−b∑i=1mαiyi+∑i=1mαi
= 1 2 w T ∑ α i y i x i − ∑ i = 1 m α i y i w T x i + ∑ i = 1 m α i \qquad\qquad\qquad=\frac{1}{2}w^T\sum\alpha_iy_ix_i-\sum^m_{i=1}\alpha_iy_iw^Tx_i+\sum^m_{i=1}\alpha_i =21wT∑αiyixi−∑i=1mαiyiwTxi+∑i=1mαi
= ∑ i = 1 m α i − 1 2 ∑ i = 1 m α i y i w T x i \qquad\qquad\qquad=\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i=1}\alpha_iy_iw^Tx_i =∑i=1mαi−21∑i=1mαiyiwTxi
= ∑ i = 1 m α i − 1 2 ∑ i , j = 1 m α i α j y i y j ( x i x j ) \qquad\qquad\qquad=\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j) =∑i=1mαi−21∑i,j=1mαiαjyiyj(xixj)
再把max问题转成min问题:
max ∑ i = 1 m α i − 1 2 ∑ i , j = 1 m α i α j y i y j ( x i x j ) = min 1 2 ∑ i , j = 1 m α i α j y i y j ( x i x j ) − ∑ i = 1 m α i \max\ \sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)=\min \frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum^m_{i=1}\alpha_i max ∑i=1mαi−21∑i,j=1mαiαjyiyj(xixj)=min21∑i,j=1mαiαjyiyj(xixj)−∑i=1mαi
s . t . ∑ i = 1 m α i y i = 0 , s.t.\ \sum^m_{i=1}\alpha_iy_i=0, s.t. ∑i=1mαiyi=0,
$ \alpha_i \geq 0,i=1,2,…,m$
以上为SVM对偶问题的对偶形式
kernel
在低维空间计算获得高维空间的计算结果,也就是说计算结果满足高维(满足高维,才能说明高维下线性可分)。
soft margin & slack variable
引入松弛变量 ξ ≥ 0 \xi\geq0 ξ≥0,对应数据点允许偏离的functional margin 的量。
目标函数: min 1 2 ∣ ∣ w ∣ ∣ 2 + C ∑ ξ i s . t . y i ( w T x i + b ) ≥ 1 − ξ i \min\ \frac{1}{2}||w||^2+C\sum\xi_i\qquad s.t.\ y_i(w^Tx_i+b)\geq1-\xi_i min 21∣∣w∣∣2+C∑ξis.t. yi(wTxi+b)≥1−ξi
对偶问题:
max ∑ i = 1 m α i − 1 2 ∑ i , j = 1 m α i α j y i y j ( x i x j ) = min 1 2 ∑ i , j = 1 m α i α j y i y j ( x i x j ) − ∑ i = 1 m α i \max\ \sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)=\min \frac{1}{2}\sum^m_{i,j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum^m_{i=1}\alpha_i max i=1∑mαi−21i,j=1∑mαiαjyiyj(xixj)=min21i,j=1∑mαiαjyiyj(xixj)−i=1∑mαi
s . t . C ≥ α i ≥ 0 , i = 1 , 2 , . . . , m ∑ i = 1 m α i y i = 0 , s.t.\ C\geq\alpha_i \geq 0,i=1,2,...,m\quad \sum^m_{i=1}\alpha_iy_i=0, s.t. C≥αi≥0,i=1,2,...,mi=1∑mαiyi=0,
Sequential Minimal Optimization
首先定义特征到结果的输出函数: u = w T x + b u=w^Tx+b u=wTx+b.
因为 w = ∑ α i y i x i w=\sum\alpha_iy_ix_i w=∑αiyixi
有 u = ∑ y i α i K ( x i , x ) − b u=\sum y_i\alpha_iK(x_i, x)-b u=∑yiαiK(xi,x)−b
max ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j < ϕ ( x i ) T , ϕ ( x j ) > \max \sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i=1}\sum^m_{j=1}\alpha_i\alpha_jy_iy_j<\phi(x_i)^T,\phi(x_j)> max∑i=1mαi−21∑i=1m∑j=1mαiαjyiyj<ϕ(xi)T,ϕ(xj)>
s . t . ∑ i = 1 m α i y i = 0 , s.t.\ \sum^m_{i=1}\alpha_iy_i=0, s.t. ∑i=1mαiyi=0,
$ \alpha_i \geq 0,i=1,2,…,m$
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline
导入数据
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
for i in range(len(data)):
if data[i,-1] == 0:
data[i,-1] = -1
# print(data)
return data[:,:2], data[:,-1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
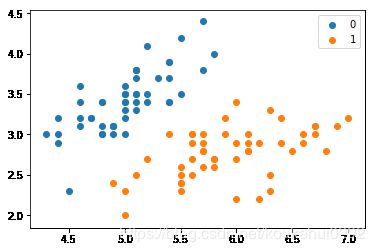
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()
训练模型
sklearn.svm.SVC
(C=1.0, kernel=‘rbf’, degree=3, gamma=‘auto’, coef0=0.0, shrinking=True, probability=False,tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None,random_state=None)
参数:
- C:C-SVC的惩罚参数C?默认值是1.0
C越大,相当于惩罚松弛变量,希望松弛变量接近0,即对误分类的惩罚增大,趋向于对训练集全分对的情况,这样对训练集测试时准确率很高,但泛化能力弱。C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
-
kernel :核函数,默认是rbf,可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’
– 线性:u’v
– 多项式:(gamma*u’*v + coef0)^degree
– RBF函数:exp(-gamma|u-v|^2)
– sigmoid:tanh(gamma*u’*v + coef0)
-
degree :多项式poly函数的维度,默认是3,选择其他核函数时会被忽略。
-
gamma : ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’,则会选择1/n_features
-
coef0 :核函数的常数项。对于‘poly’和 ‘sigmoid’有用。
-
probability :是否采用概率估计?.默认为False
-
shrinking :是否采用shrinking heuristic方法,默认为true
-
tol :停止训练的误差值大小,默认为1e-3
-
cache_size :核函数cache缓存大小,默认为200
-
class_weight :类别的权重,字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)
-
verbose :允许冗余输出?
-
max_iter :最大迭代次数。-1为无限制。
-
decision_function_shape :‘ovo’, ‘ovr’ or None, default=None3
-
random_state :数据洗牌时的种子值,int值
主要调节的参数有:C、kernel、degree、gamma、coef0。
from sklearn.svm import SVC
clf = SVC()
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
0.95999999999999996