import numpy as np
import matplotlib.pyplot as plt
# 计算距离和
def distance_sum(point, distances):
res = 0.
for index in range(len(point)-1):
res += distances[point[index]][point[index+1]]
return res
# 获取选择下一城市的权重字典
def right(begin, unvisited, matrix, distances, alpha, beta, Q):
# 计算权重
data = dict()
for end in unvisited:
data[end] = ((Q / distances[begin][end]) ** beta) * (matrix[begin][end] ** alpha)
# 权重和
s = sum(data.values())
# 权重字典
for index in unvisited:
data[index] = data[index] / s
return data
# 通过权重字典选择下一城市
def next(right_dict):
# 获取概率
p = np.random.random()
# 概率求和
ps = 0.
# 获取下一座城市
last = 0
for index in right_dict:
last = index
ps += right_dict[index]
if p < ps:
return index
return last
def ACO(x, y, m=150, n=60, alpha=1, beta=5, Q=1, rho=0.1):
# 城市数量
city_num = len(x)
# 城市编号
city = [i for i in range(city_num)]
# 构造节点
points = []
for i in city:
points.append((x[i], y[i]))
# 计算间距
distances = np.zeros((city_num, city_num))
for i in range(city_num):
for j in range(city_num):
distance = (points[i][0] - points[j][0]) ** 2 + (points[i][1] - points[j][1]) ** 2
distance = np.sqrt(distance)
distances[i][j] = distance
# 初始化最优解
pg = [i for i in range(city_num)]
# 初始化信息素浓度
pheromonetable = np.ones((city_num, city_num))
# 主循环
for i in range(m):
# 每一次主循环的蚁群路径
paths = np.zeros((city_num, city_num))
for j in range(n):
# 起点
begin = np.random.randint(0, city_num)
# 记录个体路径
temp = [begin]
# 未访问的城市列表
unvisited = city[:]
unvisited.remove(begin)
while len(unvisited) > 0:
# 计算下一个访问的城市
rights = right(begin, unvisited, pheromonetable, distances, alpha, beta, Q)
next_city = next(rights)
# 记录路径
paths[begin][next_city] += 1
temp.append(next_city)
# 设置禁忌表
unvisited.remove(next_city)
# 重置起点
begin = next_city
# 更新最优解
if distance_sum(temp, distances) < distance_sum(pg, distances):
pg = temp[:]
# 更新信息素
pheromonetable *= (1 - rho)
for v in range(city_num):
for u in range(city_num):
if v != u:
pheromonetable[v][u] += (paths[v][u] * (Q / distances[v][u]))
print((i, distance_sum(pg, distances)))
return pg
# 准备数据
number = 100
x = np.round(np.random.rand(number) * 100)
y = np.round(np.random.rand(number) * 100)
plt.plot(x, y, '.')
# 转换为点集
points = []
for i in range(number):
points.append((x[i], y[i]))
# 蚁群算法
pg = ACO(x, y)
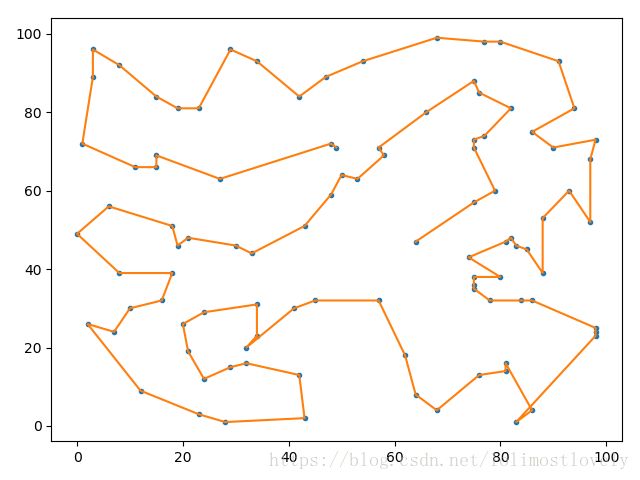
# 结果可视化
xx = []
yy = []
for i in pg:
xx.append(points[i][0])
yy.append(points[i][1])
plt.plot(xx, yy)
plt.show()
plt.cla()