【CF594E】Cutting the Line 【贪心】【Lyndon Word】【扩展kmp】

传送门

题意：给一个字符串$S$和正整数$k$，将$S$分成最多$k$段，每段不变或翻转，使得最后的字典序最小。

$|S|\le 5\times 10^6$

发现不翻转可以看成拆成若干单字符分别翻转，所以先分析一下必须翻转的情况

把原串翻转记为$S^R$，然后我们要求的是不断剪掉$S^R$的后缀然后依次拼起来

这样最终串的第一段是$S^R$的一个后缀，所以最终串的开头一定有$S^R$的最小后缀，但不一定是最小后缀作为第一段，因为最小后缀可能会在前面作为非后缀出现

显然这个“最小后缀”是Lyndon分解后的最后一段，记为$s$ 我们希望开头的$s$尽量多

那么$S^R$可表示为$a_{1}s+t_1+a_{2}s+t_2+...+a_{n}s+t_n+as$(和Lyndon分解没有关系)

首先可以一刀把$as$砍掉，然后找到$a_1\sim a_n$中最大的砍下来 发现这第二段是砍掉$as$后的最小后缀，相当于是下一轮的第一段

整理一下，对$S^R$进行Lyndon分解并合并相等段，这个Duval的时候魔改一下就可以了

然后依次砍掉最后一段并让$k-1$

注意我们假设了必须翻转，如果我们发现有连续一段的长度为$1$的串，相当于这一段不翻转，只需要一步

这个流程需要砍掉两段（只是后面一段和下一步的第一段重合了），所以需要$k>2$

完了之后有$k\le 2$,如果剩下的只有一段直接大力讨论掉

如果$k=1$,$S$和$S^R$取个$\min$即可

如果$k=2$,相当于分两段大力讨论 注意是针对原串

1. 前面后面都不翻 就是原串
2. 只翻后面

我们考虑找到最优的位置

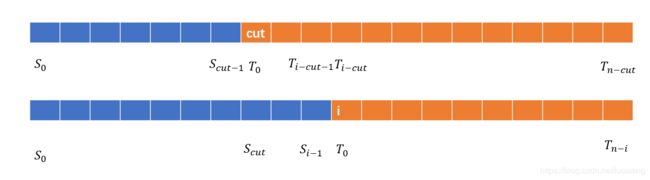
从左到右循环，设当前最优位置为$cut$,需要更新的位置为$i$ 注意$cut<i$

(橙色部分为反串，$T$指$S^R$)

我们希望比较两个串的大小 所以从$cut$开始找到第一个不同的位置比较大小

首先求出$S_{cut\sim i-1}$与$T$的最长公共前缀，可以先跑一个exKMP,求出$S$的$cut$开始的后缀与$T$的最长公共前缀后和$i-cut$取$\min$

如果把蓝色部分顶满了，再加上后面的部分

即$T$从$i-cut$开始的后缀与$T$的最长公共前缀与$n-i+1$取$\min$

然后讨论一下找到第一个不同的字符比较大小即可

3. 翻前面，后面不管

继续从$S^R$的结尾截后缀，设截取的后缀为$T$

考虑分解后的最后一个Lyndon串$s$,$T$一定以$s$开头，也以$s$结尾

根据意识流，$T$一定不会只取一个分解后的LW的一部分，也不会把两个相等的LW隔开

设$T$开始的第一段为$s^{\prime }$,所以$s$是$s^{\prime }$的前缀

然后有若干个$s^{\prime }$接在后面，这些$s^{\prime }$后的第一个设为$t$

根据Lyndon分解的定义，$t\le s^{\prime }$。而如果$t<s^{\prime }$,那么从$t$开始截取后缀会比$T$小，与定义矛盾

所以$T$一定是$s^{\prime }+s^{\prime }+...+s^{\prime }+s+s+...+s$的形式

把上面剩下的 Lyndon分解合并相等段 的倒数第二段提出来，如果$s$是它的前缀，说明倒数第二段是$s^{\prime }$，此时分类讨论翻后面两段或者只翻最后一段；如果不是说明$s^{\prime }$不存在，只能翻最后一段

第二段和反串取$\min$接在后面

复杂度$O(n)$

如果用std::string的话，要注意A=A+B和A+=B复杂度不同……

#include 
#include 
#include 
#include 
#include 
#include 
#define MAXN 10000005
using namespace std;
string s,t,ts,ans;
int pos[MAXN],len[MAXN],tot;
inline string reverse(string s)
{
	string t;
	t.resize(s.size());
	int n=s.size();
	for (int i=0;i<n;i++) t[n-i-1]=s[i];
	return t;
}
void Duval(const string& s)
{
	int n=s.size();
	for (int i=0;i<n;)
	{
		int j=i,k=i+1;
		while (s[j]<=s[k]) 
		{
			if (s[j]==s[k]) ++j;
			else j=i; 
			++k;
		}
		len[++tot]=k-j;
		while (i<=j)
		{
			pos[tot]=i+k-j-1;
			i+=k-j;
		}
	}
}
int p[MAXN];
void Exkmp(const string& s)
{
	int n=s.size();
	int mid=0,mx=0;
	p[0]=n;
	for (int i=1;i<n;i++)
	{
		if (i<=mx) p[i]=min(p[i-mid],mx-i+1);
		while (s[i+p[i]]==s[p[i]]) ++p[i];
		if (i+p[i]-1>mx) mid=i,mx=i+p[i]-1;
	}
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>s;
	t=reverse(s);
	int k;
	cin>>k;
	if (k==1) return cout<<min(s,t),0;
	Duval(t);
	pos[0]=-1;
	while (k>2&&tot)
	{
		if (len[tot]==1)
		{
			while (tot&&len[tot]==1) ans+=t.substr(pos[tot-1]+1,pos[tot]-pos[tot-1]),--tot;
			--k;
		}
		else ans+=t.substr(pos[tot-1]+1,pos[tot]-pos[tot-1]),--k,--tot;
	}
	if (tot==0) return cout<<ans,0;
	if (tot==1)
	{
		string tmp=t.substr(0,pos[1]+1);
		tmp=min(tmp,reverse(tmp));
		cout<<ans+tmp;
		return 0;
	}
	s=reverse(t=t.substr(0,pos[tot]+1));
	ts=t+"#"+s;
	Exkmp(ts);
	string tmp=min(s,t);
	int cut=0,n=s.size();
	for (int i=1;i<n;i++)
	{
		int cl=min(i-cut,p[n+1+cut]);
		if (cut+cl==i) cl+=p[cl];
		cl=min(cl,n-cut);
		if ((cl<i-cut? s[cut+cl]:t[cut+cl-i])<t[cl]) cut=i;
	}
	tmp=min(tmp,s.substr(0,cut)+t.substr(0,n-cut));
	string las=t.substr(pos[tot-1]+1,len[tot]);
	string lass=t.substr(pos[tot-2]+1,len[tot]);
	int st=pos[tot-1]+1;
	string tt=t.substr(st,n-st);
	string res=t.substr(0,n-tt.size());
	tt+=min(res,reverse(res));
	tmp=min(tmp,tt);
	if (las==lass)
	{
		st=pos[tot-2]+1;
		tt=t.substr(st,n-st);
		res=t.substr(0,n-tt.size());
		tt=tt+min(res,reverse(res));
		tmp=min(tmp,tt);
	}
	cout<<ans+tmp;
	return 0;
}