剑指offer题集分类 Python实现详解

剑指offer题集分类归纳

一: 链表（5道）

面试题18：删除链表的节点

简单

给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。

返回删除后的链表的头节点。

注意：此题对比原题有改动

示例 1:

输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 4 -> 1 -> 9.

尾节点法:

#Definition for singly-linked list.
#class ListNode:
#    def __init__(self, x):
#       self.val = x
#        self.next = None

class Solution:
    def deleteNode(self, head: ListNode, val: int) -> ListNode:
        dummy = ListNode(0)  # 设置伪结点
        dummy.next = head
        if head.val == val: 
            return head.next # 头结点是要删除的点，直接返回
        while head and head.next:
            if head.next.val == val # 找到了要删除的结点，删除
                head.next = head.next.next
                return dummy.next
            else:
                head = head.next

双指针法：

class Solution:   
   def deleteNode(self, head: ListNode, val: int) -> ListNode:
        if not head:
            return head
        
        if head.val == val:
            return head.next
        
        pre = head
        cur = head.next

        while cur:
            if cur.val == val:
                pre.next = cur.next
                return head
            
            else:    #删除节点为尾节点的情况
                pre = cur
                cur = cur.next

复杂度分析：
时间复杂度 O(N) ： N 为链表长度，删除操作平均需循环 N/2次，最差 N次。
空间复杂度 O(1) ： cur, pre 占用常数大小额外空间。

。

面试题22 [ 链表中倒数第k个节点]

简单

输入一个链表，输出该链表中倒数第k个节点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾节点是倒数第1个节点。例如，一个链表有6个节点，从头节点开始，它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个节点是值为4的节点。

给定一个链表: 1->2->3->4->5, 和 k = 2.

返回链表 4->5.

双指针法：

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getKthFromEnd(self, head: ListNode, k: int) -> ListNode:
        former, latter = head, head
        for _ in range(k):
            former = former.next

        while former:
            former, latter = former.next, latter.next
        return latter

复杂度分析：
时间复杂度 O(N)O(N) ： NN 为链表长度；总体看， former 走了 NN 步， latter 走了 (N-k)(N−k) 步。
空间复杂度 O(1)O(1) ： 双指针 former , latter 使用常数大小的额外空间。

面试题24. [反转链表]

难度：简单

定义一个函数，输入一个链表的头节点，反转该链表并输出反转后链表的头节点。

示例:

输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        preNode = None
        currNode = head
        while currNode:
            nextNode = currNode.next #用nextNode记录currNode的指向
            currNode.next = preNode  #关键步骤 反转箭头
            preNode = currNode  
            currNode = nextNode
        return preNode

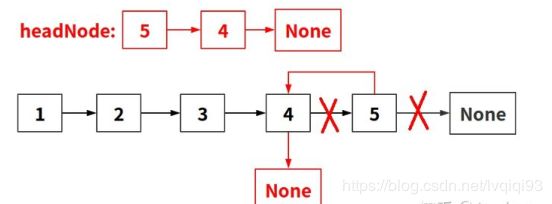
1.首先函数进入开头的两个if语句，分别是用来判断当前节点和下一个节点是否为NULL，尤其是第二个,在后面递归过程中也会用到。

2.然后开始进入递归，注意传给 self.reverseList( ) 的参数为 head.next ,也就是说链表的会一直往后传递，直到找到最后一个节点（也就是head.val *==* 5的节点，后文简述为节点5）。此时，因为不满足第二个if语句，返回节点5。

3.函数在第二步返回到递归的上一层，headNode 等于返回的节点5 , 也就是节点5作为反转的链表头，完成反转的第一步。

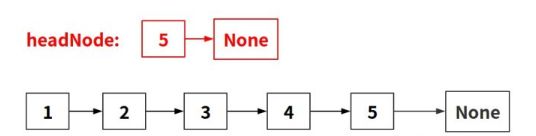
4. 当前节点head为节点4 , head.next指向节点5， head.next.next指向None。 head.next.next= head 让原来指向None的节点5，改为指向节点4，完成了5—>None到5—>4的反转；然后head.next = None , 作用在于截断节点4到节点5的指针，避免形成4—>5—>4的环。

5.同理，返回上一层，当前节点head为节点3，让节点4指向节点3，再截断节点3到节点4的指针。

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        if not head or not head.next:  # 递归中止条件
            return head
     
        headNode = self.reverseList(head.next)
        head.next.next = head
        head.next = None
        return headNode

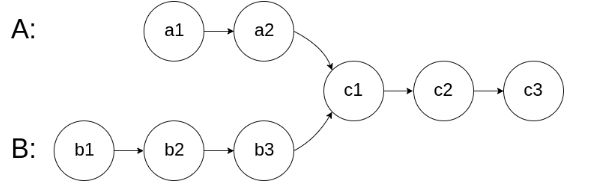
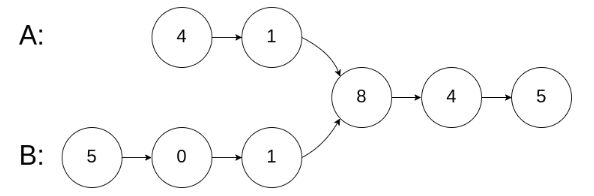
[面试题52. 两个链表的第一个公共节点]

难度：简单

输入两个链表，找出它们的第一个公共节点。

如下面的两个链表：

在节点 c1 开始相交。

示例 1：

输入：intersectVal = 8,  listA = [4,1,8,4,5],  listB = [5,0,1,8,4,5],  skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

双指针法：

解题思路：
我们使用两个指针 node1，node2 分别指向两个链表 headA，headB 的头结点，然后同时分别逐结点遍历，当 node1 到达链表 headA 的末尾时，重新定位到链表 headB 的头结点；当 node2 到达链表 headB 的末尾时，重新定位到链表 headA 的头结点。

这样，当它们相遇时，所指向的结点就是第一个公共结点。

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
        a1, b1 = headA, headB

        while a1 != b1:
            a1 = a1.next if a1 else headB
            b1 = b1.next if b1 else headA 
        return a1

复杂度分析

- 时间复杂度：O(M+N) 。
- 空间复杂度：O(1)。

[面试题35. 复杂链表的复制] (不会)

难度中等

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

示例 1：

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

二 数组（5道）

[面试题03. 数组中重复的数字]

难度简单

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3 

class Solution:

    def findRepeatNumber(self, nums: List[int]) -> int:
        index = 0
        while index < len(nums):
            if nums[index] == index:
                index += 1
            else:
                if nums[index] == nums[nums[index]]:
                    return nums[index]
                else:
                    nums[nums[index]], nums[index] = nums[index], nums[nums[index]]
     return -1

说明：题目中给出了数组的长度范围，因此不需要对数组的长度做非空判断。

复杂度分析：

时间复杂度：O(N) ，这里 N是数组的长度。虽然 for 循环里面套了 while，但是每一个数来到它应该在的位置以后，位置就不会再变化。这里用到的是均摊复杂度分析的方法：如果在某一个位置 while 循环体执行的次数较多，那么一定在后面的几个位置，根本不会执行 while 循环体内的代码，也就是说最坏的情况不会一直出现。也就是说最坏复杂度的情况不会一直出现。
空间复杂度：O(1) 。

[面试题04. 二维数组中的查找]

难度简单

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        if len(matrix) == 0:
            return False
        row = len(matrix) - 1
        column = len(matrix[0]) - 1

        i = row
        j = 0

        while i >= 0 and j <= column:
            if target < matrix[i][j]:
                i -= 1
            elif target > matrix[i][j]:
                j += 1
            else:
                return True
        return False

复杂度分析：
时间复杂度 O(M+N) ：其中，N 和 M 分别为矩阵行数和列数，此算法最多循环 M+N 次。
空间复杂度 O(1) : i, j 指针使用常数大小额外空间。

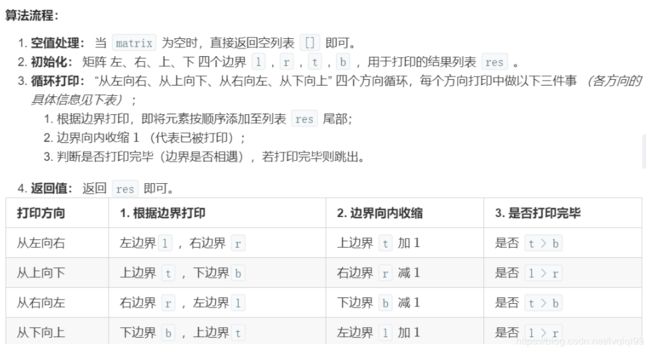
[面试题29. 顺时针打印矩阵]

难度简单

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

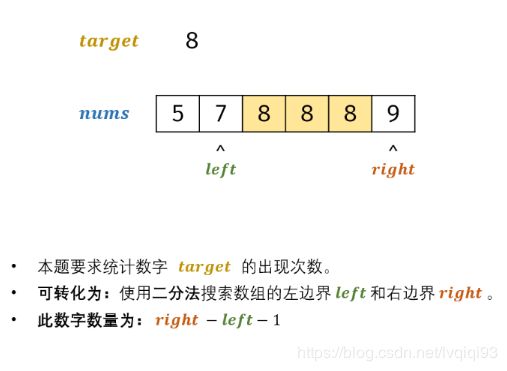
[面试题53 - I. 在排序数组中查找数字 I]

难度简单

统计一个数字在排序数组中出现的次数。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2

"二分法"
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        i = 0
        j = len(nums) - 1
         # 搜索右边界 right
        while i <= j:
            m = (i + j)//2
            if nums[m] <= target:
                i = m + 1
            else:
                j = m - 1
        right = i

        # 若数组中无 target ，则提前返回
        if j >= 0 and nums[j] != target:
            return 0

         # 搜索左边界 right
        i = 0
        while i <= j:
            m = (i + j)//2
            if nums[m] < target: #注意边界条件 没有=才能确定左边界
                i = m + 1
            else:
                j = m - 1
        left = j

        return right-left-1
        
        

复杂度分析：

• 时间复杂度 O(log N) ： 二分法为对数级别复杂度。
• 空间复杂度 O(1）： 几个变量使用常数大小的额外空间。

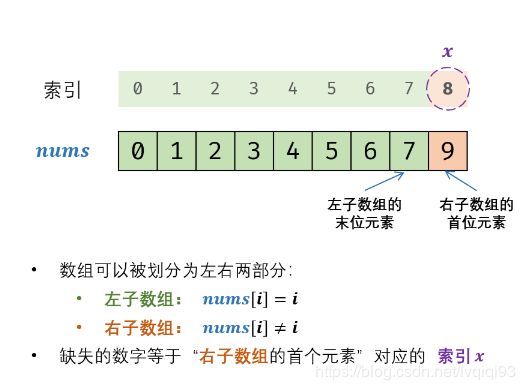
[面试题53 - II. 0～n-1中缺失的数字]

难度简单

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

示例 1:

输入: [0,1,3]
输出: 2

“排序数组中的搜索问题，首先想到 二分法 解决。"

class Solution:
    def missingNumber(self, nums: List[int]) -> int:
        i = 0
        j = len(nums) - 1
        while i <= j:
            m = (i + j) // 2
            if nums[m] == m: # 关键
                i = m + 1
            else:
                j = m - 1
        return i

杂度分析：

• 时间复杂度 O(log N) ： 二分法为对数级别复杂度。
• 空间复杂度 O(1)： 几个变量使用常数大小的额外空间。

[面试题29. 顺时针打印矩阵]

难度简单

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

思路：

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if matrix == []:
            return []
        
        a = 0
        b = 0
        c = len(matrix) - 1
        d = len(matrix[0]) - 1

        res = []
        while True:
            for i in range(b,d+1):
               res.append(matrix[a][i]) 
            a += 1
            if b > d:
                break
                    

            for i in range(a,c+1):
                res.append(matrix[i][d])                    
            d -= 1
            if a > c:
                break 

            for i in range(d,b-1,-1):
                res.append(matrix[c][i])
            c -= 1
            if b > d:
                break

            for i in range(c,a-1,-1):
                res.append(matrix[i][b])
            b += 1
            if a > c:
                break 

        return res

复杂度分析：
时间复杂度 O(MN) ： M, N 分别为矩阵行数和列数。
空间复杂度 O(1)： 四个边界 l , r , t , b 使用常数大小的 额外 空间（ res 为必须使用的空间）。

三：字符串（3道）

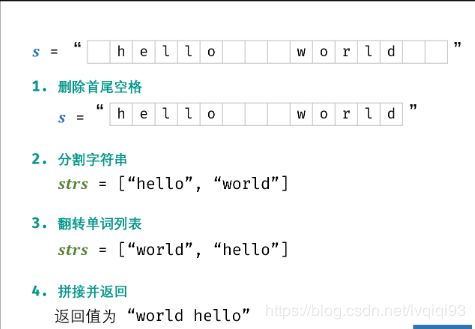
[面试题58 - I. 翻转单词顺序]

难度简单

输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串"I am a student. “，则输出"student. a am I”。

示例 1：

输入: "the sky is blue"
输出: "blue is sky the"

方法一：双指针
算法解析：
倒序遍历字符串 s ，记录单词左右索引边界 i , j ；
每确定一个单词的边界，则将其添加至单词列表 res ；
最终，将单词列表拼接为字符串，并返回即可。

复杂度分析：
时间复杂度 O(N) ： 其中 N 为字符串 s 的长度，线性遍历字符串。

空间复杂度 O(N) ： 新建的 list(Python) 或 StringBuilder(Java) 中的字符串总长度 N≤N ，占用 O(N) 大小的额外空间。

class Solution:
   
    def reverseWords(self, s: str) -> str:
        s = s.strip() # 删除首尾空格
        i = j = len(s) - 1
        res = []
        while i >= 0:
            while i >= 0 and s[i] != ' ': 
                i -= 1 # 搜索首个空格
            res.append(s[i + 1: j + 1]) # 添加单词

            while i >= 0 and s[i] == ' ': 
                i -= 1 # 跳过单词间空格
            j = i # j 指向下个单词的尾字符

        return ' '.join(res) # 拼接并返回

方法二：分割 + 倒序
利用 “字符串分割”、“列表倒序” 的内置函数 （面试时不建议使用） ，可简便地实现本题的字符串翻转要求。

算法解析：
Python ： 由于 split()split() 方法将单词间的 “多个空格看作一个空格” （参考自 split()和split(’ ')的区别 ），因此不会出现多余的 “空单词” 。因此，直接利用 reverse()reverse() 方法翻转单词列表 strsstrs ，拼接为字符串并返回即可。

class Solution:
    def reverseWords(self, s: str) -> str:
        s = s.strip() # 删除首尾空格
        strs = s.split() # 分割字符串
        strs.reverse() # 翻转单词列表
        return ' '.join(strs) # 拼接为字符串并返回

或者一行：

class Solution:
    def reverseWords(self, s: str) -> str:
        return ' '.join(s.strip().split()[::-1]) 

复杂度分析：
时间复杂度O(N) ： 总体为线性时间复杂度，各函数时间复杂度和参考资料链接如下。
split() 方法： 为 O(N) ；
trim() 和 strip() 方法： 最差情况下（当字符串全为空格时），为 O(N) ；
join() 方法： 为 O(N)；
reverse() 方法： 为 O(N) ；
空间复杂度 O(N)： 单词列表 strs 占用线性大小的额外空间。

[面试题58 - II. 左旋转字符串]

难度简单

字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如，输入字符串"abcdefg"和数字2，该函数将返回左旋转两位得到的结果"cdefgab"。

示例 1：

输入: s = "abcdefg", k = 2
输出: "cdefgab"

方法一：字符串切片
应用字符串切片函数，可方便实现左旋转字符串。

获取字符串 s[n:] 切片和 s[:n] 切片，使用 “++” 运算符拼接并返回即可。

复杂度分析：
时间复杂度 O(N) ： 其中 N为字符串 s 的长度，字符串切片函数为线性时间复杂度（参考资料）；
空间复杂度 O(N) ： 两个字符串切片的总长度为 N 。

PythonJava
class Solution:
    def reverseLeftWords(self, s: str, n: int) -> str:
        return s[n:] + s[:n]

方法二：列表遍历拼接
若面试规定不允许使用 切片函数 ，则使用此方法。

算法流程：
新建一个 list(Python)、StringBuilder(Java) ，记为 res ；
先向 res 添加 “第 n + 1 位至末位的字符” ；
再向 res添加 “首位至第 n 位的字符” ；
将 res 转化为字符串并返回。
复杂度分析：
时间复杂度 O(N)： 线性遍历 s 并添加，使用线性时间；
空间复杂度 O(N) ： 新建的辅助 res使用 O(N) 大小的额外空间。

代码：

class Solution:
    def reverseLeftWords(self, s: str, n: int) -> str:
        res = []
        for i in range(n, len(s)):
            res.append(s[i])
        for i in range(n):
            res.append(s[i])
        return ''.join(res)

利用求余运算，可以简化代码。

class Solution:
    def reverseLeftWords(self, s: str, n: int) -> str:
        res = []
        for i in range(n, n + len(s)):
            res.append(s[i % len(s)])
        return ''.join(res)

方法三：字符串遍历拼接
若规定 Python 不能使用 join() 函数，或规定 Java 只能用 String ，则使用此方法。

此方法与 方法二 思路一致，区别是使用字符串代替列表。

复杂度分析：
时间复杂度 O(N) ： 线性遍历 s 并添加，使用线性时间；
空间复杂度 O(N) ： 假设循环过程中内存会被及时回收，内存中至少同时存在长度为 N 和 N-1 的两个字符串（新建长度为 N 的 res 需要使用前一个长度 N-1 的 res ），因此至少使用 O(N) 的额外空间。

class Solution:
    def reverseLeftWords(self, s: str, n: int) -> str:
        res = ""
        for i in range(n, len(s)):
            res += s[i]
        for i in range(n):
            res += s[i]
        return res

同理，利用求余运算，可以简化代码。

class Solution:
    def reverseLeftWords(self, s: str, n: int) -> str:
        res = ""
        for i in range(n, n + len(s)):
            res += s[i % len(s)]
        return res

效率分析：

以上三种方法的空间使用如下图所示。

因为字符串是不可变对象，所以方法二申请一次额外内存，但方法三申请N次额外内存。

[面试题67. 把字符串转换成整数]

难度中等

写一个函数 StrToInt，实现把字符串转换成整数这个功能。不能使用 atoi 或者其他类似的库函数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。

当我们寻找到的第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字组合起来，作为该整数的正负号；假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成整数。

该字符串除了有效的整数部分之后也可能会存在多余的字符，这些字符可以被忽略，它们对于函数不应该造成影响。

注意：假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换。

在任何情况下，若函数不能进行有效的转换时，请返回 0。

说明：

假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围，请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。

示例 1:

输入: "42"
输出: 42

示例 2:

输入: "   -42"
输出: -42
解释: 第一个非空白字符为 '-', 它是一个负号。
     我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。

示例 3:

输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 '3' ，因为它的下一个字符不为数字。

示例 4:

输入: "words and 987"
输出: 0
解释: 第一个非空字符是 'w', 但它不是数字或正、负号。
     因此无法执行有效的转换。

示例 5:

输入: "-91283472332"
输出: -2147483648
解释: 数字 "-91283472332" 超过 32 位有符号整数范围。 
     因此返回 INT_MIN (−231) 。

class Solution:
    def strToInt(self, str: str) -> int:
    
        str = str.strip() # 删除首尾空格
        if not str: 
            return 0 # 字符串为空则直接返回 易遗忘
        res = 0
        i = 1
        sign = 1
        max_int = 2 ** 31 - 1
        
        if str[0] == '-': 
            sign = -1 # 保存负号
        elif str[0] != '+': 
            i = 0 # 若无符号位，则需从 i = 0 开始数字拼接
            
        for c in str[i:]:
            if not '0' <= c <= '9' : 
                break # 遇到非数字的字符则跳出
            res = 10 * res + ord(c) - ord('0') # 数字拼接
            if res > max_int: 
                return max_int if sign == 1 else -max_int - 1 # 数字越界处理
        return sign * res

复杂度分析：
时间复杂度 O(N) ： 其中 N 为字符串长度，线性遍历字符串占用 O(N) 时间。
空间复杂度 O(N) ： 删除首尾空格后需建立新字符串，最差情况下占用 O(N) 额外空间。

四：栈（4道）

[面试题09. 用两个栈实现队列]

难度简单

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

输入：
["CQueue","appendTail","deleteHead","deleteHead"]
[[],[3],[],[]]
输出：[null,null,3,-1]

思路：

双栈可实现列表倒序： 设有含三个元素的栈 A = [1,2,3] 和空栈 B = [ ]。若循环执行 A 元素出栈并添加入栈 B ，直到栈 A 为空，则 A = [ ], B = [3,2,1] ，即 栈 B 元素实现栈 A 元素倒序 。
利用栈 B 删除队首元素： 倒序后，B 执行出栈则相当于删除了 A 的栈底元素，即对应队首元素。

加入队尾 appendTail( ) 函数： 将数字 val 加入栈 A 即可。
删除队首 deleteHead( ) 函数： 有以下三种情况：

• 当栈 B 不为空： B中仍有已完成倒序的元素，因此直接返回 B 的栈顶元素。
• 否则，当 A 为空： 即两个栈都为空，无元素，因此返回 -1 。
• 否则： 将栈 A 元素全部转移至栈 B 中，实现元素倒序，并返回栈 B 的栈顶元素。

class CQueue:

    def __init__(self):
        self.inStack = []
        self.outStack = []

    def appendTail(self, value: int) -> None:
        self.inStack.append(value)

    def deleteHead(self) -> int:
        if self.outStack:
            return self.outStack.pop()
        if not self.inStack:
            return -1
        while self.inStack:
            self.outStack.append(self.inStack.pop())
        return self.outStack.pop()

[面试题30. 包含min函数的栈]

难度简单

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.min();   --> 返回 -2.

思路：

增加一个栈，以空间换时间

class MinStack:

    def __init__(self):
        """
        initialize your data structure here.
        """
        self.stack = []
        self.min_stack = []


    def push(self, x: int) -> None:
        """stack每加入一个元素，min_stack也加入一个元素，
        将min_stack的栈顶与stack此时加入的元素比较,加入小的那个"""
        
        self.stack.append(x)

        if self.min_stack:
            if self.min_stack[-1] <= x:
                self.min_stack.append(self.min_stack[-1])
            else:
                self.min_stack.append(x)
        else:
            self.min_stack.append(x)


    def pop(self) -> None:
        if not self.stack:
            return None
        
        self.stack.pop()
        self.min_stack.pop()


    def top(self) -> int:
        if not self.stack:
            return None

        return self.stack[-1]

    # min_stack的栈顶永远是此时栈中的最小元素
    def min(self) -> int:
        if not self.min_stack:
            return None

        return self.min_stack[-1]

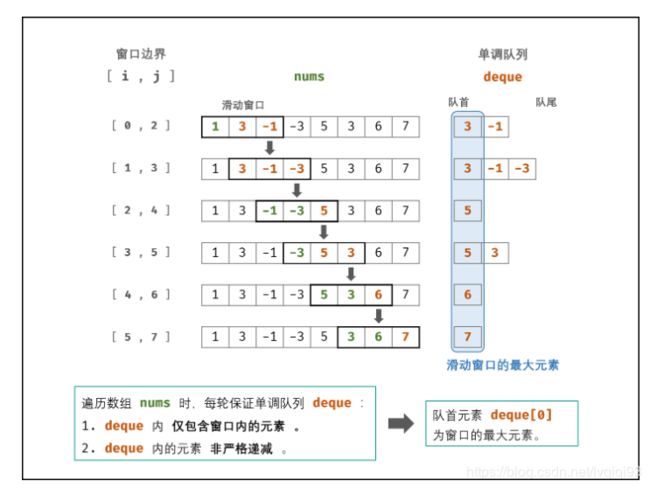
[面试题59 - I. 滑动窗口的最大值]

难度简单

给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

算法流程：

1. 初始化： 双端队列 deque ，结果列表 res ，数组长度 n ；

2. 滑动窗口： 左边界范围 i∈[1−k,n+1−k] ，右边界范围 j∈[0,n−1] ；

   1.队首元素 deque[0] 不在当前窗口范围之内，元素出队；
   2.删除 deque 内所有 < nums[j] 的元素，以保持 deque 递减；
   3.将 nums[j] 添加至 deque 尾部；
   4.若已形成窗口（即 i≥0 ）：将窗口最大值（即队首元素 deque[0] ）添加至列表 res 。

3. 返回值： 返回结果列表 res

注：Python 通过 zip(range(), range()) 可实现滑动窗口的左右边界 i, j 同时遍历。

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        deque = collections.deque()
        res = []
         n = len(nums)

        for i, j in zip(range(1 - k, n + 1 - k), range(n)):
            if i > 0 and deque[0] == nums[i - 1]: 
                deque.popleft() # 删除 deque 中对应的 nums[i-1]
            while deque and deque[-1] < nums[j]: 
                deque.pop() # 保持 deque 递减， 0 位置一定是窗口最大值
            deque.append(nums[j])
            if i >= 0: 
                res.append(deque[0]) # 记录窗口最大值

        return res

复杂度分析：
时间复杂度 O(n) ： 其中 n 为数组 nums 长度；线性遍历 nums 占用 O(N) ；每个元素最多仅入队和出队一次，因此单调队列 deque 占用 O(2N) 。
空间复杂度 O(k) ： 双端队列 deque 中最多同时存储 k 个元素（即窗口大小）。

[面试题59 - II. 队列的最大值]

难度中等

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

import queue
class MaxQueue:

    def __init__(self):
        self.deque = queue.deque()  # 双端队列是为了存储最大值，最大值永远在队首
        self.queue = queue.Queue()


    def max_value(self) -> int:
        return self.deque[0] if self.deque else -1


    def push_back(self, value: int) -> None:
        while self.deque and self.deque[-1] < value:
            self.deque.pop()
        
        self.deque.append(value)
        self.queue.put(value)


    def pop_front(self) -> int:
        if not self.deque :
            return -1
        ans = self.queue.get()
        # 当双端队列和队列的队首数字一样时，需要删掉双端队列的队首，因为不存在就不可能是最大值了
        if ans == self.deque[0]: 
            self.deque.popleft()

        return ans

复杂度分析:

时间复杂度：O(1) （插入，删除，求最大值）
删除操作于求最大值操作显然只需要 O(1) 的时间。
而插入操作虽然看起来有循环，做一个插入操作时最多可能会有 n 次出队操作。但要注意，由于每个数字只会出队一次，因此对于所有的 n 个数字的插入过程，对应的所有出队操作也不会大于 n 次。因此将出队的时间均摊到每个插入操作上，时间复杂度为 O(1) 。
空间复杂度：O(n) ，需要用队列存储所有插入的元素。

五：树(14道)

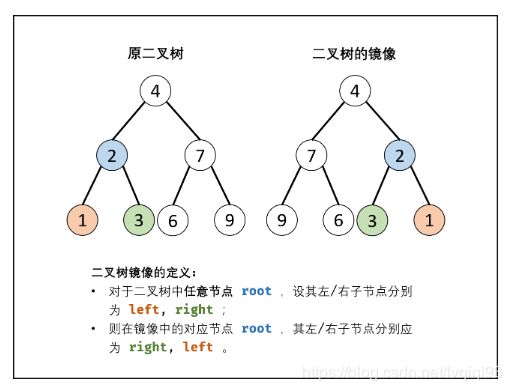
[面试题27. 二叉树的镜像]

难度简单

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

方法一：递归法
根据二叉树镜像的定义，考虑递归遍历（dfs）二叉树，交换每个节点的左 / 右子节点，即可生成二叉树的镜像。
递归解析：
终止条件： 当节点 root 为空时（即越过叶节点），则返回 null ；
递推工作：
初始化节点 tmp ，用于暂存 root 的左子节点；
开启递归 右子节点 mirrorTree(root.right) ，并将返回值作为 root 的 左子节点 。
开启递归 左子节点 mirrorTree(tmp) ，并将返回值作为 root 的 右子节点 。
返回值： 返回当前节点 rootroot ；
Q： 为何需要暂存 rootroot 的左子节点？
A： 在递归右子节点 “root.left = mirrorTree(root.right);root.left=mirrorTree(root.right);” 执行完毕后， root.leftroot.left 的值已经发生改变，此时递归左子节点 mirrorTree(root.left)mirrorTree(root.left) 则会出问题。

复杂度分析：
时间复杂度 O(N) ： 其中 N 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用 O(N) 时间。
空间复杂度 O(N) ： 最差情况下（当二叉树退化为链表），递归时系统需使用 O(N)大小的栈空间。
代码：
Python 利用平行赋值的写法（即 a, b = b, a ），可省略暂存操作。其原理是先将等号右侧打包成元组 (b,a) ，再序列地分给等号左侧的 a, b 序列。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def mirrorTree(self, root):
        if not root:
            return 
        root.left, root.right = self.mirrorTree(root.right), self.mirrorTree(root.left)
        return root

方法二：辅助栈（或队列）
利用栈（或队列）遍历树的所有节点 node ，并交换每个 node 的左 / 右子节点。
算法流程：

1. 特例处理： 当 root 为空时，直接返回 null ；
2. 初始化： 栈（或队列），本文用栈，并加入根节点 root 。
3. 循环交换： 当栈 stack 为空时跳出；

• 出栈： 记为 node ；
• 添加子节点： 将 node 左和右子节点入栈；
• 交换： 交换 node 的左 / 右子节点。

4.返回值： 返回根节点 root 。

class Solution(object):
    def mirrorTree(self, root):
        if not root:
            return 
        stack = [root]
        while stack:
            node = stack.pop()
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
            node.left, node.right =  node.right, node.left 
        return root

复杂度分析：
时间复杂度 O(N) ： 其中 N 为二叉树的节点数量，建立二叉树镜像需要遍历树的所有节点，占用 O(N) 时间。
空间复杂度 O(N) ： 最差情况下（当为满二叉树时），栈 stack 最多同时存储 N/2 个节点，占用 O(N) 额外空间。

[面试题28. 对称的二叉树]

难度简单

请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

递归方法：

算法流程：
isSymmetric(root) ：

特例处理： 若根节点 root 为空，则直接返回 true 。
返回值： 即 recur(root.left, root.right) ;
recur(L, R) ：

终止条件：
当 L 和 R 同时越过叶节点： 此树从顶至底的节点都对称，因此返回 true ；
当 L或 R 中只有一个越过叶节点： 此树不对称，因此返回 false ；
当节点 L 值 ！= 节点 R 值： 此树不对称，因此返回 false ；
递推工作：
判断两节点 L.left和 R.right是否对称，即 recur(L.left, R.right) ；
判断两节点 L.right和 R.left 是否对称，即 recur(L.right, R.left) ；
返回值： 两对节点都对称时，才是对称树，因此用与逻辑符 && 连接。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
   def isSymmetric(self, root):

       def recur(L, R):
           if not L and not R: 
               return True
           if not L or not R or L.val != R.val:  # val易错
               return False
           return recur(L.left, R.right) and recur(L.right, R.left)

       return recur(root.left, root.right) if root else True

复杂度分析：

时间复杂度 O(N) ： 其中 N 为二叉树的节点数量，每次执行 recur() 可以判断一对节点是否对称，因此最多调用 N/2 次 recur() 方法。
空间复杂度 O(N) ： 最差情况下，二叉树退化为链表，系统使用 O(N) 大小的栈空间。

[面试题55 - I. 二叉树的深度]

难度简单

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

方法一：后序遍历（DFS）
树的后序遍历 / 深度优先搜索往往利用 递归 或 栈 实现，本文使用递归实现。
关键点： 此树的深度和其左（右）子树的深度之间的关系。显然，此树的深度 等于 左子树的深度 与 右子树的深度 中的 最大值 +1 。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
   def maxDepth(self, root):
       if not root:
           return 0
       return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

复杂度分析：
时间复杂度 O(N) ： N 为树的节点数量，计算树的深度需要遍历所有节点。
空间复杂度 O(N) ： 最差情况下（当树退化为链表时），递归深度可达到 N 。

[面试题55 - II. 平衡二叉树]

难度简单

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7

返回 true 。

方法一：先序遍历 + 判断深度 （从顶至底）
此方法容易想到，但会产生大量重复计算，时间复杂度较高。

思路是构造一个获取当前子树的深度的函数 depth(root) （即 面试题55 - I. 二叉树的深度 ），通过比较某子树的左右子树的深度差 abs(depth(root.left) - depth(root.right)) <= 1 是否成立，来判断某子树是否是二叉平衡树。若所有子树都平衡，则此树平衡。

算法流程：
isBalanced(root) 函数： 判断树 root 是否平衡

特例处理： 若树根节点 root 为空，则直接返回 true e ；
返回值： 所有子树都需要满足平衡树性质，因此以下三者使用与逻辑 && 连接；
abs(self.depth(root.left) - self.depth(root.right)) <= 1 ：判断 当前子树 是否是平衡树；
self.isBalanced(root.left) ： 先序遍历递归，判断 当前子树的左子树 是否是平衡树；
self.isBalanced(root.right) ： 先序遍历递归，判断 当前子树的右子树 是否是平衡树；
depth(root) 函数： 计算树 root 的深度

终止条件： 当 root 为空，即越过叶子节点，则返回高度 0 ；
返回值： 返回左 / 右子树的深度的最大值 +1 。

复杂度分析：
时间复杂度 O(N log N) ： 最差情况下（为 “满二叉树” 时）， isBalanced(root) 遍历树所有节点，判断每个节点的深度 depth(root) 需要遍历 各子树的所有节点 。
满二叉树按层分为 log (N+1) 层；
通过调用 depth(root) ，判断二叉树各层的节点的对应子树的深度，（每层开始，最多遍历 N 个节点，最少遍历 $(N+1)/2$ 个节点）。

因此，总体时间复杂度 == 每层执行复杂度 × 层数复杂度 = O(N×logN) 。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isBalanced(self, root):
        if not root:
            return True
        return abs(self.depth(root.left)-self.depth(root.right)) <=1 and self.isBalanced(root.left) and self.isBalanced(root.right)

    def depth(self,root):
        if not root:
            return 0
        return max(self.depth(root.left),self.depth(root.right)) + 1
        

方法二：后序遍历 + 剪枝 （从底至顶）
此方法为本题的最优解法，但剪枝的方法不易第一时间想到。

思路是对二叉树做后序遍历，从底至顶返回子树深度，若判定某子树不是平衡树则 “剪枝” ，直接向上返回。

算法流程：
recur(root) 函数：

返回值：
当节点root 左 / 右子树的深度差 ≤1 ：则返回当前子树的深度，即节点 root 的左 / 右子树的深度最大值 +1 （ max(left, right) + 1 ）；
当节点root 左 / 右子树的深度差 > 2 ：则返回 −1 ，代表 此子树不是平衡树 。
终止条件：
当 root 为空：说明越过叶节点，因此返回高度 0 ；
当左（右）子树深度为 -1 ：代表此树的 左（右）子树 不是平衡树，因此剪枝，直接返回 −1 ；
isBalanced(root) 函数：

返回值： 若 recur(root) != -1 ，则说明此树平衡，返回 true ； 否则返回 false 。

复杂度分析：
时间复杂度 O(N) ： N 为树的节点数；最差情况下，需要递归遍历树的所有节点。
空间复杂度 O(N) ： 最差情况下（树退化为链表时），系统递归需要使用 O(N) 的栈空间。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isBalanced(self, root):
        def recur(root):
            if not root:
                return 0
            left = recur(root.left)
            if left == -1:
                return -1
            right = recur(root.right)
            if right == -1:
                return -1
            return max(left,right)+1 if abs(left-right) <= 1 else -1
        
        return recur(root) != -1

[面试题68 - I. 二叉搜索树的最近公共祖先]

难度简单

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。

思路：

如果在同一侧，向着那一侧走到下一个节点，继续比较。如果在根节点的两侧，则一定根节点就是最近的公共祖先。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        while root:
            if root.val < p.val and root.val < q.val:
                root = root.right
            if root.val > p.val and root.val > q.val:
                root = root.left
            else:
                break
        return root

复杂度分析：
时间复杂度 O(N) ： 其中 N 为二叉树节点数；每循环一轮排除一层，二叉搜索树的层数最小为 logN （满二叉树），最大为 N （退化为链表, 一颗二叉树只有左子树，没有右子树，就是链表）。
空间复杂度 O(1) ： 使用常数大小的额外空间。

[面试题68 - II. 二叉树的最近公共祖先] （不会）

难度简单

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

解法1：递归
这是一道纯递归题，递归很好想到，关键就是边界条件的处理。

【思路】

递归解析：

终止条件：
当越过叶节点，则直接返回 null ；
当 root 等于 p, q ，则直接返回 root ；

递推工作：
开启递归左子节点，返回值记为 left ；
开启递归右子节点，返回值记为 right ；

返回值： 根据 left 和 right ，可展开为四种情况；

1.当 left 和 right 同时为空 ：说明 root 的左 / 右子树中都不包含 p,q ，返回 null ；
2.当 left 和 right 同时不为空 ：说明 p, q 分列在 root 的 异侧 （分别在 左 / 右子树），因此 root 为最近公共祖先，返回 root ；
3.当 left 为空 ，right不为空 ：p,q 都不在 root 的左子树中，直接返回 right 。具体可分为两种情况：
3.1 p,q 其中一个在 root 的 右子树 中，此时 right 指向 p（假设为 p ）；
3.2 p,q 两节点都在 root 的 右子树 中，此时的 right 指向 最近公共祖先节点 ；
4.当 left 不为空 ， right 为空 ：与情况 3. 同理；

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
   def lowestCommonAncestor(self, root, p, q):
       if not root or root == p or root == q: 
           return root
       left = self.lowestCommonAncestor(root.left, p, q)
       right = self.lowestCommonAncestor(root.right, p, q)
       # 当 left 和 right 同时不为空:说明p, q分列在root的异侧, root 为最近公共祖先，返回 root  
       if not left: 
           return right
       if not right: 
           return left
           
       return root

复杂度分析：
时间复杂度 O(N) ： 其中 N 为二叉树节点数；最差情况下，需要递归遍历树的所有节点。
空间复杂度 O(N) ： 最差情况下，递归深度达到 N ，系统使用 O(N) 大小的额外空间。

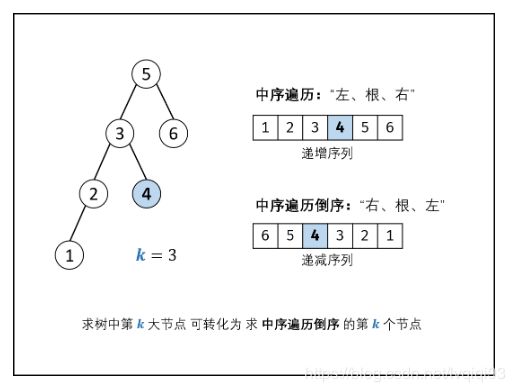
[面试题54. 二叉搜索树的第k大节点] (不会)

难度简单26

给定一棵二叉搜索树，请找出其中第k大的节点。

示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

递归解析：
1.终止条件： 当节点 root 为空（越过叶节点），则直接返回；
2.递归右子树： 即 dfs(root.right) ；

3.三项工作：
提前返回： 若 k = 0 ，代表已找到目标节点，无需继续遍历，因此直接返回；
统计序号： 执行 k = k - 1 （即从 k 减至 0 ）；
记录结果： 若 k = 0 ，代表当前节点为第 k 大的节点，因此记录 res = root.val ；

4.递归左子树： 即 dfs(root.left) ；

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def kthLargest(self, root, k):
        def dfs(root):
            if not root: 
                return
            dfs(root.right)
            if self.k == 0: 
                return
            self.k -= 1
            if self.k == 0: 
                self.res = root.val
            dfs(root.left)

        self.k = k
        dfs(root)
        return self.res

复杂度分析：
时间复杂度 O(N) ： 当树退化为链表时（全部为右子节点），无论 k 的值大小，递归深度都为 N ，占用 O(N) 时间。
空间复杂度 O(N) ： 当树退化为链表时（全部为右子节点），系统使用 O(N) 大小的栈空间。

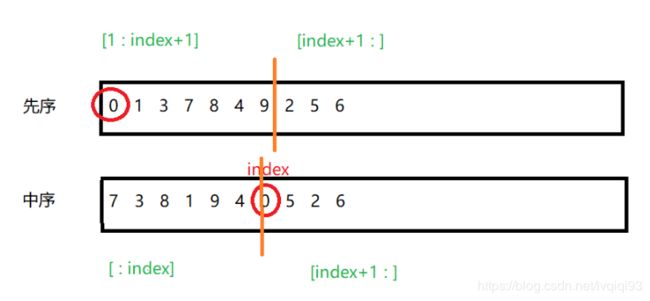
面试题07. 重建二叉树

难度中等

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, pre, tin):
        #pre是前序遍历 tin是中序遍历 not pre 和not tin效果一样，因为这两个序列长度一样
        if not pre :
            return None 

        root = TreeNode(pre[0]) #根节点一定是pre的第一个数   
        # 中序遍历时候root的下标    
        index = tin.index(root.val)        
        # 对于中序便利的数组tin
        # tin的 [0:index] 为左子树的中序遍历序列
        # tin的 [index+1:] 右子树的中序遍历序列

        root.left = self.buildTree(pre[1:index+1],tin[:index]) #pre去掉第一个根节点
        root.right = self.buildTree(pre[index+1:],tin[index+1:])

        return root

复杂度分析：

时间复杂度 O(N) ：递归共建立 N 个节点，每层递归中的节点建立、搜索操作占用 O(1) ，因此递归占用 O(N)（最差情况为所有子树只有左节点，树退化为链表，此时递归深度 O(N)）

空间复杂度 O(N) ： 递归操作中系统需使用 O(N)额外空间。

面试题26. 树的子结构（不会）

难度中等47

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

recur(A, B) 函数：

终止条件：
1.当节点 B 为空：说明树 BB 已匹配完成（越过叶子节点），因此返回 true；
2.当节点 A 为空：说明已经越过树 AA 叶子节点，即匹配失败，返回 false；
3.当节点 A 和 B 的值不同：说明匹配失败，返回 false ；
返回值：
1.判断 A 和 B 的左子节点是否相等，即 recur(A.left, B.left) ；
2.判断 A 和 B 的右子节点是否相等，即 recur(A.right, B.right) ；

isSubStructure(A, B) 函数：

特例处理： 当 树 A 为空 或 树 B 为空 时，直接返回 false ；
返回值： 若树 BB 是树 AA 的子结构，则必满足以下三种情况之一，因此用或 || 连接；
1.以 节点 A 为根节点的子树 包含树 B ，对应 recur(A, B)；
2.树 B 是 树 A 左子树 的子结构，对应 isSubStructure(A.left, B)；
3.树 B 是 树 A右子树 的子结构，对应 isSubStructure(A.right, B)；
以上 2. 3. 实质上是在对树 A 做 先序遍历 。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def isSubStructure(self, A, B):
        """
        :type A: TreeNode
        :type B: TreeNode
        :rtype: bool
        """
        def recur(A, B):
            if not B: 
                return True
            if not A or A.val != B.val: 
                return False
            return recur(A.left, B.left) and recur(A.right, B.right)

        return bool(A and B) and (recur(A, B) or self.isSubStructure(A.left, B) or self.isSubStructure(A.right, B))

复杂度分析：
时间复杂度 O(MN) ： 其中 M,N 分别为树 A 和 树 B 的节点数量；先序遍历树 A 占用 O(M) ，每次调用 recur(A, B) 判断占用 O(N) 。
空间复杂度 O(M) ： 当树 A和树 B都退化为链表时，递归调用深度最大。当 M≤N 时，遍历树 A 与递归判断的总递归深度为 M ；当 M>N时，最差情况为遍历至树 A叶子节点，此时总递归深度为 M。

面试题32 - I. 从上到下打印二叉树

难度中等16

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回：

[3,9,20,15,7]

解题思路：

• 题目要求的二叉树的 从上至下 打印（即按层打印），又称为二叉树的 广度优先搜索（BFS）。
• BFS 通常借助 队列 的先入先出特性来实现。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
 
class Solution(object):
    def levelOrder(self, root):
        if not root: 
            return []
        res = []
        queue = collections.deque()
        queue.append(root)
        while queue:
            node = queue.popleft()
            res.append(node.val)
            if node.left: 
                queue.append(node.left)
            if node.right: 
                queue.append(node.right)
        return res
 

复杂度分析：
时间复杂度 O(N) ： N 为二叉树的节点数量，即 BFS 需循环 N 次。
空间复杂度 O(N) ： 最差情况下，即当树为平衡二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 O(N) 大小的额外空间。

代码：
Python 中使用 collections 中的双端队列 deque() ，其 popleft() 方法可达到 O(1) 时间复杂度；列表 list 的 pop(0) 方法时间复杂度为 O(N) 。

面试题32 - II. 从上到下打印二叉树 II

难度简单21

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [9,20],
  [15,7]
]

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def levelOrder(self, root):
        if not root :
            return []
        res = []
        queue = collections.deque()
        queue.append(root)

        while queue:
            tmp = []
            for _ in range(len(queue)):
                node = queue.popleft()
                tmp.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            res.append(tmp)
        return res
            

复杂度分析：
时间复杂度 O(N) ： N 为二叉树的节点数量，即 BFS 需循环 N 次。
空间复杂度 O(N) ： 最差情况下，即当树为平衡二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 O(N) 大小的额外空间。

面试题32 - III. 从上到下打印二叉树 III

难度中等18

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回其层次遍历结果：

[
  [3],
  [20,9],
  [15,7]
]

方法一：层序遍历 + 倒序
此方法的优点是只用列表即可，无需其他数据结构。
偶数层倒序： 若 res 的长度为 奇数 ，说明当前是偶数层，则对 tmp 执行 倒序 操作。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def levelOrder(self, root):
        if not root :
            return []
        res = []
        queue = collections.deque()
        queue.append(root)

        while queue:
            tmp = []
            for _ in range(len(queue)):
                node = queue.popleft()
                tmp.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            res.append(tmp[::-1] if len(res)%2 else tmp ) # 关键一行
        return res

复杂度分析：
时间复杂度 O(N) ： N 为二叉树的节点数量，即 BFS 需循环 N 次，占用 O(N) 。共完成 少于 N 个节点的倒序操作，占用 O(N) 。
空间复杂度 O(N) ： 最差情况下，即当树为满二叉树时，最多有 N/2 个树节点同时在 queue 中，使用 O(N) 大小的额外空间。

方法二：层序遍历 + 双端队列

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root: return []
        res, deque = [], collections.deque([root])
        while deque:
            tmp = collections.deque()
            for _ in range(len(deque)):
                node = deque.popleft()
                if len(res) % 2: 
                    tmp.appendleft(node.val) # 偶数层 -> 队列头部
                else: 
                    tmp.append(node.val) # 奇数层 -> 队列尾部
                if node.left: deque.append(node.left)
                if node.right: deque.append(node.right)
            res.append(list(tmp))
        return res
 

面试题34. 二叉树中和为某一值的路径

难度中等34

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

示例:
给定如下二叉树，以及目标和 sum = 22，

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \    / \
        7    2  5   1

返回:

[
   [5,4,11,2],
   [5,8,4,5]
]

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def pathSum(self, root, sum):

        res, path = [], []
        def recur(root, tar):
            if not root: 
                return
            path.append(root.val)
            tar -= root.val
            if tar == 0 and not root.left and not root.right:
                res.append(list(path))
                
            recur(root.left, tar)
            recur(root.right, tar)
            path.pop()

        recur(root, sum)
        return res

复杂度分析：
时间复杂度 O(N) ： N 为二叉树的节点数，先序遍历需要遍历所有节点。
空间复杂度 O(N) ： 最差情况下，即树退化为链表时，path 存储所有树节点，使用 O(N) 额外空间。
代码：
值得注意的是，记录路径时若直接执行 res.append(path) ，则是将 path 对象加入了 res ；后续 path 改变时， res 中的 path 对象也会随之改变。

正确做法：res.append(list(path)) ，相当于复制了一个 path 并加入到 res 。

面试题37. 序列化二叉树（不会）

难度困难

请实现两个函数，分别用来序列化和反序列化二叉树。

示例:

你可以将以下二叉树：

    1
   / \
  2   3
     / \
    4   5

序列化为 "[1,2,3,null,null,4,5]"

思路：先序遍历

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:
#序列化
    def serialize(self, root):
        if not root:
            return 'null'
        s = str(root.val) + ',' + self.serialize(root.left) + ',' +  self.serialize(root.right)
        return s
        
#反序列化
    def deserialize(self, data):
        list = data.split(',')
        return self.deserializeTree(list)


#递归部分
    def deserializeTree(self, list):
        if len(list) <= 0:
            return None
        val = list.pop(0)
        root = None
        if val != 'null':
            root = TreeNode(int(val))
            root.left = self.deserializeTree(list)
            root.right = self.deserializeTree(list)
        return root   

复杂度分析：
时间复杂度 O(N) ： N 为二叉树的节点数，遍历需要访问所有节点，最差情况下需要访问 N + 1 个 null 总体复杂度为 O(2N + 1) = O(N)
空间复杂度 O(N)

六：排序：

面试题45. 把数组排成最小的数

难度中等46

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。

示例 1:

输入: [10,2]
输出: "102"

示例 2:

输入: [3,30,34,5,9]
输出: "3033459"

思路：冒泡排序

X+Y > Y+X 则：X>Y

class Solution(object):
    def minNumber(self, nums):
        n = len(nums)
        if n == 0:
            return ""
        for i in range(n):
            nums[i] = str(nums[i])
        for i in range(n):
            for j in range(i+1,n):
                if nums[i]+nums[j]>nums[j]+nums[i]:
                    nums[i],nums[j]=nums[j],nums[i]
        return "".join(nums)
                

**时间复杂度：**O(N^2)

优化：快排：O(NlogN）

七：堆

面试题40. 最小的k个数

难度简单85

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：

输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：

输入：arr = [0,1,2,1], k = 1
输出：[0]

class Solution(object):
    def getLeastNumbers(self, arr, k):
        if k == 0:
            return list()
        hp = [-x for x in arr[:k]]
        heapq.heapify(hp)
        for i in range(k,len(arr)):
            if -hp[0] > arr[i]:
                heapq.heappop(hp)
                heapq.heappush(hp,-arr[i])
        ans = [-x for x in hp]
        return ans

复杂度分析

时间复杂度： O(nlogk)，其中 n 是数组 arr 的长度。由于大根堆实时维护前 k 小值，所以插入删除都是 O(logk) 的时间复杂度，最坏情况下数组里 n 个数都会插入，所以一共需要 O(nlogk) 的时间复杂度。

空间复杂度：O(k) ，因为大根堆里最多 k 个数。

面试题41. 数据流中的中位数

难度困难26

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

• void addNum(int num) - 从数据流中添加一个整数到数据结构中。
• double findMedian() - 返回目前所有元素的中位数。

class MedianFinder(object):

    def __init__(self):
        self.min_heap = []
        self.max_heap = []    


    def addNum(self, num):
        if len(self.min_heap) == len(self.max_heap):
            heappush(self.max_heap, -num)
            heappush(self.min_heap, -heappop(self.max_heap))
        else:
            heappush(self.min_heap, num)
            heappush(self.max_heap, -heappop(self.min_heap))

    def findMedian(self):
        if len(self.min_heap) == len(self.max_heap):
            return (self.min_heap[0]-self.max_heap[0])/2
        else:
            return self.min_heap[0]

复杂度分析：
时间复杂度：
查找中位数 O(1) ： 获取堆顶元素使用 O(1) 时间；
添加数字 O(log N) ： 堆的插入和弹出操作使用 O(logN) 时间。
空间复杂度 O(N) ： 其中 N 为数据流中的元素数量，小顶堆 A 和大顶堆 B 最多同时保存 N 个元素。
代码：
Python 中 heapq 模块是小顶堆。实现 大顶堆 方法： 小顶堆的插入和弹出操作均将元素 取反 即可。
Java 使用 PriorityQueue<>((x, y) -> (y - x)) 可方便实现大顶堆。