[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)
非线性方程数值求解
(1)单变量非线性方程求解
函数的调用格式为:
x=fzerof(filename,x0)
其中,filename是待求根方程左端的函数表达式,x0是初始值。

>> f=@(x) x-1./x+5;
>> x1=fzero(f,-5)
x1 =
-5.1926
>> x2=fzero(f,1)
x2 =
0.1926
>> x3=fzero(f,0.1)
x3 =
3.7372e-016
>>
>> f=@(x) x.^2-1;
>> x=[];
>> x0=-0.25:0.001:0.25;
>> for x00 = x0
x=[x,fzero(f,x00)];
end
>> plot(x0,x,'-o')
>> xlabel('初值');
>> ylabel('方程的根');
>> axis([-0.25,0.25,-1,1])
>>
x=fsolve(filename,x0,option)
其中,x为返回的近似解,filename是待求根方程左端的函数表达式,x0是初值,option用于设置优化工具箱的优化参数,可以调用optimset函数来完成。
看起来有两种函数可以求解非线性方程组,但是如何在使用中找取最关键的解决方案呢?这里采用了跟线性方程组迭代法一样的测试方案,同时再对例1求解!(现在采用fsolve函数)
>> f=@(x) x-1./x+5;
>> x1=fsolve(f,-5,optimset('Display','off'))
x1 =
-5.1926
>> x2=fsolve(f,1,optimset('Display','off'))
Warning: Divide by zero.
> In @(x) x-1./x+5
In optim\private\trustnleqn at 210
In fsolve at 295
x2 =
0.1926
>> x3=fsolve(f,0.1,optimset('Display','off'))
x3 =
0.1926
>>
相信各位已经发现,报了一个warnning,说明两个函数实现方法不同,采取的计算步数也不同,希望同学们认真理解运用,方能体会出真正的细微行差异!
![[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)_第3张图片](http://img.e-com-net.com/image/info8/b00b208cd3a048f5bec99702586f94f0.jpg)
>> f=@(x) [sin(x(1))+x(2)+x(3)^2*exp(x(1)),x(1)+x(2)+x(3),x(1)*x(2)*x(3)];
>> f([1,1,1])
ans =
4.5598 3.0000 1.0000
>> x=fsolve(f,[1,1,1],optimset('Display','off'))
x =
0.0224 -0.0224 -0.0000
>> f(x)
ans =
1.0e-006 *
-0.5931 -0.0000 0.0006
>>
有些同学感觉这道题说的不是很舒服,其实题目的意思很明确让你在一个区间内取出满足方程组的解,这时候同fsolve就可以解决啦!
函数极值得计算
- 最大值
- 最小值
这里仅讨论最小值。为什么?因为最小值的添个负号就是最大值
(1)无约束最优化问题
求最小值的函数:
[xmin,fmin]=fminbnd(filename,x1,x2,option)
[xmin,fmin]=fminsearch(filename,x0,option)
[xmin,fmin]=fminunc(filename,x0,option)
其中,filename是定义的目标函数。第一个函数的输入变量x1、x2分别表示被研究区间的左、右边界。后两个函数的输入变量x0是一个向量,表示极值点的初值。option为优化参数,可以通过optimset函数来设置。
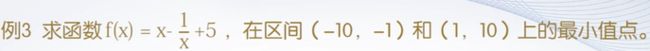
>> f=@(x) x-1./x+5;
>> [xmin,fmin]=fminbnd(f,-10,-1)
xmin =
-10
fmin =
-4.9000
>> [xmin,fmin]=fminbnd(f,1,10)
xmin =
1
fmin =
5
(2)有约束最优化问题
有约束最优化问题的一般描述为:
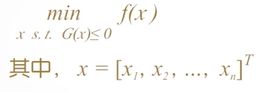
约束条件可细化为:
- 线性不等式约束
- 线性等式约束
- 非线性不等式约束
- 非线性等式约束
- X的上界和下界
(2)有约束最优化问题
求有约束条件下最小值的函数为:
[xmin,fmin]=fmincon(filename,x0,A,b,Aeq,beq,Lbnd,Ubnd,NonF,option)
其中,xmin、fmin、filename、x0和option的含义与求最小值函数相同。其余参数为约束条件,包括线性不等式约束、线性等式约束、x的下界和上界以及定义非线性约束的函数。如果某个约束不存在,则用空矩阵来表示。
![[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)_第4张图片](http://img.e-com-net.com/image/info8/bcc1e168fbc94a80b048c099658f6bdf.jpg)
f=@(x) 0.4*x(2)+x(1)^2+x(2)^2-x(1)*x(2)+1/30*x(1)^3;
x0=[0.5;0.5];
A=[-1,-0.5;-0.5,-1];
b=[-0.4;-0.5];
lb=[0;0];
option=optimset('Display','off');
[xmin,fmin]=fmincon(f,x0,A,b,[],[],lb,[],[],option)
(3)最小值问题应用实例
例5 某公司有A、B、C、D、E5个工厂,分别位于xy平面上的坐标点(10,10),(30,50),(16.667,29),(0.555,29.888)和(22.2221,49.988)处。设两点之间的距离表示在工厂之间开车的距离,以公里为单位。公司计划在平面上某点处建造一座仓库,预期平均每周到A、B、C、D、E工厂分别有10、18、20、14和25次送货。理想情况下,要使每周送货车的里程最小、仓库应建在xy平面的什么位置?
建立约束条件、目标函数即可得出相应方程,下面给出目标函数
![[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)_第5张图片](http://img.e-com-net.com/image/info8/b185a679ab8e4434b92f47d69af6e613.jpg)
>> a=[10,30,16.667,0.555,22.2221];%%横坐标
>> b=[10,50,29,29.888,49.988];%%纵坐标
>> c=[10,18,20,14,25];%%运送次数
>> f=@(x) sum(c.*sqrt((x(1)-a).^2+(x(2)-b).^2));%%目标函数
>> [xmin,fmin]=fminsearch(f,[15,30])
xmin =
19.8143 41.1247
fmin =
1.3618e+003
>>
>> [xmin,fmin]=fmincon(f,[15,30],[],[],[],[],[],[],'funny')
Warning: Large-scale (trust region) method does not currently solve this type of problem,
switching to medium-scale (line search).
> In fmincon at 260
Optimization terminated: Magnitude of directional derivative in search
direction less than 2*options.TolFun and maximum constraint violation
is less than options.TolCon.
xmin =
5.9363 35.2401
fmin =
1.6676e+003
>>
>> f=@(x) [x(1)-0.6*sin(x(1))-0.3*cos(x(2)),x(2)-0.6*(cos(x(1)))+0.3*sin(x(2))];
>> x=fsolve(f,[0.5,0.5],optimset('Display','off'))
x =
0.6354 0.3734
>>
改编,套用,老师从来不指望学生能写出高深的代码,一切基础性的学习只为通向更专业的知识领域!
![[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)_第1张图片](http://img.e-com-net.com/image/info8/0c89a8f363064a67b5b47cf8a55b78a3.jpg)
![[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)_第2张图片](http://img.e-com-net.com/image/info8/01062c617cac4e55882e315bc7f282e0.jpg)

![[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)_第6张图片](http://img.e-com-net.com/image/info8/13bb1a43ca4f47d983d2a1b66a88e9bf.jpg)
![[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)_第7张图片](http://img.e-com-net.com/image/info8/9693c413f39840b9a7c0048e1a7ded4e.jpg)
![[MATLAB]非线性方程求解与函数极值计算(fsolve fminunc fzero fminsearch)_第8张图片](http://img.e-com-net.com/image/info8/f5ad7e73755c4536a7f63ce1517c505c.jpg)