图网络学习理论和实践(deepwalk,node2vec,metapath2vec,EGES)

本文主要记录一些经典的基于随机游走Graph Embedding方法，以及自己的一些实践经验。

引言

在NLP领域，关于如何对词进行更好的表示，有许多研究者进行了深入的研究。

a. 独热表示（one-hot representation）

将每一个表示成一个N维（N是词表大小）的向量，其中只有当前词对应的维度为1，其他为零。一般来说词表会比较大（至少是十万量级），因此高维稀疏的表示会导致维数灾难。还有一个重要的问题是，独热表示无法描述词与词之间的相似性，也就是我们常说的语义鸿沟。

b. 分布式表示（distributed representation）

既然独热表示有这么大的问题，总是需要去解决的。于是人们提出了分布式表示，即用低维稠密的向量来表示。低维稠密向量解决维度过高的问题；同时稠密向量可以计算向量之间的距离（相似度），解决语义鸿沟问题。
既然我们想通过低维稠密的向量来表示词，那么接下来就是用什么方法得到我们想要的向量了。要相信方法总是比问题多的，我在此列举一些经典的预训练词向量方法：word2vec、glove、ELMo、GPT以及BERT等等。

c. 图和embedding？

在很多场景下，业务问题可以抽象成图结构，如搜索点击二部图、社交网络、交通网络、电商网站中用户与物品的关系等。

1.deepwalk

deepwalk是14年KDD paper: DeepWalk：Online Learning of Social Representations
核心思路： 1) 在图中随机游走采样，获取节点序列；2) 使用skip-gram + Hierarchical Softmax方式学习节点表达向量。

1.1 随机游走

1.2 向量学习

把每条游走后的序列当作句子，每个节点看作一次词，利用skip-gram语言模型进行学习，且采用Hierarchical Softmax提升训练效率。

2.node2vec

node2vec是16年KDD paper: node2vec: Scalable Feature Learning for Networks
整体思路和deepwalk一致，可以看作是deepwalk的改进版。主要对deepwalk的随机游走策略进行了改进，可以看作是引入DFS和BFS随机游走的deepwalk。

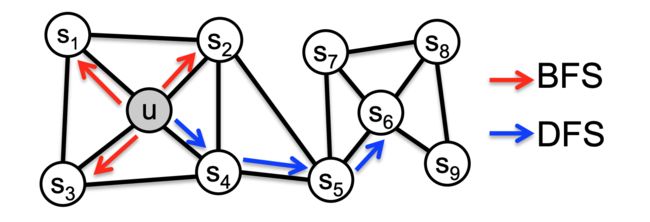
2.1 DFS和BFS随机游走

node2vec采用的是一种有偏的随机游走，给定当前顶点 $v$，访问下一个顶点 $x$ 的概率为 $P(c_i=x|c_{i-1}=v)$

其中${\pi }_{vx}={\alpha }_{p,q}(t,x)\ast w_{vx}$，且 $w_{vx}$ 是顶点 $v$ 和 $x$之间的边权重，${\alpha }_{p,q}(t,x)$是表示DFS、BFS游走策略。

$d_{tx}$为顶点 $t$ 和顶点 $x$ 之间的最短路径距离

2.2 参数p、q对游走策略的影响

Return parameter：p
参数 $p$ 控制重复访问刚刚访问过的顶点的概率(即$d_{tx}=0$时)，若 $p$ 较大，则访问刚刚访问过的顶点的概率越低，反之越高。

In-out papameter：q
参数 $q$ 控制着游走偏向，如果$q>1$ ，随机游走倾向于BFS；若$q<1$ ，随机游走倾向于DFS。

2.3 node2vec学习同质性和结构性

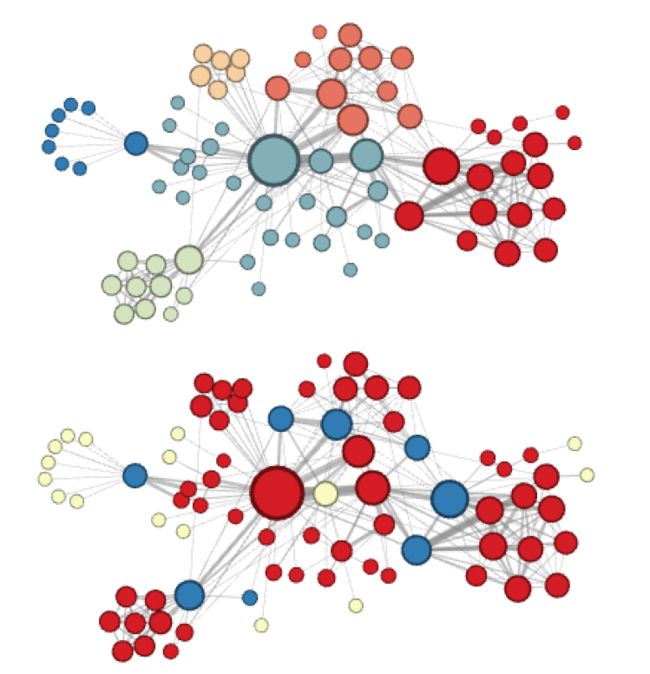
同质性指的是距离相近节点的embedding应该尽量近似，例如节点u和s1、s2、s3、s4应该属于同质性相似的节点；
结构性指的是结构上相似的节点的embedding应该尽量接近，例如节点u和节点s6应该属于结构性相似的节点。

上图是DFS结果，下图是BFS结果，颜色接近的节点代表其embedding的相似性更强。

2.4 向量学习

游走完得到节点序列后，向量学习的方法和deepwalk方式一致，在此不做赘述。

3.metapath2vec

metapath2vec是17年KDD paper: metapath2vec: Scalable Representation Learning for Heterogeneous Networks

上面所介绍的deepwalk，node2vec等算法虽然可以用于网络表示学习，但仅适合那些只包含一类顶点类型和边类型的同构网络（Homogeneous Networks），并不能很好地用于包含多种顶点类型和边类型的复杂关系网络。于是作者在基于meta-path的基础上，提出了能很好应对指定scheme结构的异构复杂关系网络的表示学习方法。

3.1 Meta-Path-Based Random Walks

在同构网络中，DeepWalk和node2vec等算法通过随机游走的方式来构建Skip-Gram模型的上下文语料库。论文作者提出了一种基于meta-path的随机游走方式，本质上就是游走过程中将节点类型做为约束。

3.2 Heterogeneous negative sampling

模型依然是skip-gram结构，将word2vec原版的negative sampling改进为Heterogeneous negative sampling，即负样本不再是从所有节点中选取，而是从某一特定类别的节点中进行随机选取。

4.EGES

EGES是18年KDD paper: Billion-scale commodity embedding for e-commerce recommendation in alibaba

主要亮点：引入节点的side information。

主要流程如下面两张图所示：

总结对比

方法	核心思路	code
deepwalk(2014 KDD)	随机游走+skip-gram	python原版 、c++版
node2vec(2016 KDD)	基于DFS和BFS的随机游走+skip-gram	原版、斯坦福snap
metapath2vec(2017 KDD)	基于meta-path的异构网络随机游走，Heterogeneous negative sampling	原版
EGES(2018 KDD)	用户行为序列构成有向图，引入节点的side information	python实现版