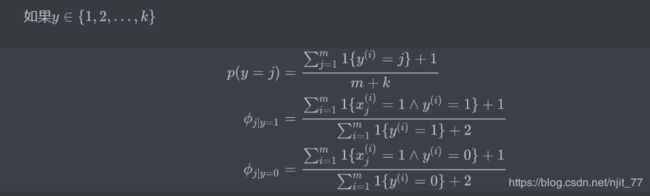生成学习算法(Generative Learning algorithms)
看了一下斯坦福大学公开课:机器学习教程(吴恩达教授),记录了一些笔记,写出来以便以后有用到。笔记如有误,还望告知。
本系列其它笔记:
线性回归(Linear Regression)
分类和逻辑回归(Classification and logistic regression)
广义线性模型(Generalized Linear Models)
生成学习算法(Generative Learning algorithms)
生成学习算法(Generative Learning algorithms)
之前我们学习的算法 p ( y ∣ x ; θ ) p(y|x;\theta) p(y∣x;θ)给定x的y的条件分布,我们称之为判别学习算法(discriminative learning algorithms);现在我们学习相反的算法 p ( x ∣ y ) ( p ( y ) ) p(x|y)(p(y)) p(x∣y)(p(y)),称之为生成学习算法(generative
learning algorithms)。
使用贝叶斯定理,我们可以得到给定x后y的分布:
p ( y ∣ x ) = p ( x ∣ y ) p ( y ) p ( x ) p ( x ) = p ( x ∣ y = 1 ) p ( y = 1 ) + p ( x ∣ y = 0 ) p ( y = 0 ) p(y|x) = \frac{p(x|y)p(y)}{p(x)} \\p(x) = p(x|y = 1)p(y = 1) + p(x|y = 0)p(y = 0) p(y∣x)=p(x)p(x∣y)p(y)p(x)=p(x∣y=1)p(y=1)+p(x∣y=0)p(y=0)
1 高斯判别分析(Gaussian discriminant analysis)
1.1 多元高斯分布(多元正态分布)
假设输入特征 x ∈ R n x \in \R^n x∈Rn,且是连续的;p(x|y)满足高斯分布。
假设z符合多元高斯分布 z ∽ N ( μ ⃗ , Σ ) z \backsim\mathcal{N}(\vec\mu,\Sigma) z∽N(μ,Σ)
p ( z ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(z) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}\exp(-\frac{1}{2}(x-\mu)^{T}\Sigma^{-1}(x-\mu)) p(z)=(2π)2n∣Σ∣211exp(−21(x−μ)TΣ−1(x−μ))
1.2 高斯判别分析模型(The Gaussian Discriminant Analysis model)
y ∽ B e r n o u l l i ( ϕ ) x ∣ y = 0 ∽ N ( μ 0 , Σ ) x ∣ y = 1 ∽ N ( μ 1 , Σ ) p ( y ) = ϕ y ( 1 − ϕ ) 1 − y p ( x ∣ y = 0 ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 exp ( − 1 2 ( x − μ 0 ) T Σ − 1 ( x − μ 0 ) ) p ( x ∣ y = 1 ) = 1 ( 2 π ) n 2 ∣ Σ ∣ 1 2 exp ( − 1 2 ( x − μ 1 ) T Σ − 1 ( x − μ 1 ) ) y \backsim Bernoulli(\phi) \\x|y = 0 \backsim\mathcal{N}(\mu_0,\Sigma) \\x|y = 1 \backsim\mathcal{N}(\mu_1,\Sigma) \\p(y) = \phi^{y}(1-\phi)^{1-y} \\p(x|y = 0) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}\exp(-\frac{1}{2}(x-\mu_0)^{T}\Sigma^{-1}(x-\mu_0)) \\p(x|y = 1) = \frac{1}{(2\pi)^{\frac{n}{2}}|\Sigma|^{\frac{1}{2}}}\exp(-\frac{1}{2}(x-\mu_1)^{T}\Sigma^{-1}(x-\mu_1)) y∽Bernoulli(ϕ)x∣y=0∽N(μ0,Σ)x∣y=1∽N(μ1,Σ)p(y)=ϕy(1−ϕ)1−yp(x∣y=0)=(2π)2n∣Σ∣211exp(−21(x−μ0)TΣ−1(x−μ0))p(x∣y=1)=(2π)2n∣Σ∣211exp(−21(x−μ1)TΣ−1(x−μ1))
ℓ ( ϕ , μ 0 , μ 1 , Σ ) = log ∏ i = 1 m p ( x ( i ) , y ( i ) ; ϕ , μ 0 , μ 1 , Σ ) = log ∏ i = 1 m p ( x ( i ) ∣ y ( i ) ; μ 0 , μ 1 , Σ ) ⋅ p ( y ( i ) ; ϕ ) → j o i n t L i k e l i h o o d = ∑ i = 1 m ( log p ( x ( i ) ∣ y ( i ) ; μ 0 , μ 1 , Σ ) + log p ( y ( i ) ; ϕ ) ) \ell(\phi,\mu_0,\mu_1,\Sigma) = \log\prod_{i=1}^{m}p(x^{(i)},y^{(i)};\phi,\mu_0,\mu_1,\Sigma) \\ = \log\prod_{i=1}^{m}p(x^{(i)}|y^{(i)};\mu_0,\mu_1,\Sigma)\cdot p(y^{(i)};\phi) \rightarrow joint \ Likelihood \\ = \sum_{i=1}^{m}(\log p(x^{(i)}|y^{(i)};\mu_0,\mu_1,\Sigma)+ \log p(y^{(i)};\phi)) ℓ(ϕ,μ0,μ1,Σ)=logi=1∏mp(x(i),y(i);ϕ,μ0,μ1,Σ)=logi=1∏mp(x(i)∣y(i);μ0,μ1,Σ)⋅p(y(i);ϕ)→joint Likelihood=i=1∑m(logp(x(i)∣y(i);μ0,μ1,Σ)+logp(y(i);ϕ))
∂ ∂ ϕ ℓ ( ϕ , μ 0 , μ 1 , Σ ) = ∂ ∂ ϕ ∑ i = 1 m ( log p ( x ( i ) ∣ y ( i ) ; μ 0 , μ 1 , Σ ) + log p ( y ( i ) ; ϕ ) ) = ∑ i = 1 m ∂ ∂ ϕ log p ( y ( i ) ; ϕ ) = ∑ i = 1 m ∂ ∂ ϕ ( y ( i ) log ( ϕ ) + ( 1 − y ( i ) ) log ( 1 − ϕ ) ) = ∑ i = 1 m ( y ( i ) − ϕ ϕ ( 1 − ϕ ) ) 令 ∂ ∂ ϕ ℓ ( ϕ , μ 0 , μ 1 , Σ ) = 0 ⇒ ϕ = ∑ i = 1 m y ( i ) m = 1 m ∑ i = 1 m 1 { y ( i ) = 1 } \left.\frac{\partial}{\partial\phi}\right.\ell(\phi,\mu_0,\mu_1,\Sigma) = \left.\frac{\partial}{\partial\phi}\right.\sum_{i=1}^{m}(\log p(x^{(i)}|y^{(i)};\mu_0,\mu_1,\Sigma)+ \log p(y^{(i)};\phi)) \\ = \sum_{i=1}^{m}\left.\frac{\partial}{\partial\phi}\right.\log p(y^{(i)};\phi) \\ = \sum_{i=1}^{m}\left.\frac{\partial}{\partial\phi}\right.(y^{(i)}\log(\phi) + (1-y{(i)})\log(1-\phi)) \\ = \sum_{i=1}^{m}(\frac{y^{(i)} - \phi}{\phi(1 - \phi)}) \\ 令 \ \left.\frac{\partial}{\partial\phi}\right.\ell(\phi,\mu_0,\mu_1,\Sigma) = 0 \Rightarrow \phi = \frac{\sum_{i=1}^{m}y^{(i)}}{m} = \frac{1}{m}\sum_{i=1}^{m}1 \lbrace y^{(i)} = 1 \rbrace ∂ϕ∂ℓ(ϕ,μ0,μ1,Σ)=∂ϕ∂i=1∑m(logp(x(i)∣y(i);μ0,μ1,Σ)+logp(y(i);ϕ))=i=1∑m∂ϕ∂logp(y(i);ϕ)=i=1∑m∂ϕ∂(y(i)log(ϕ)+(1−y(i))log(1−ϕ))=i=1∑m(ϕ(1−ϕ)y(i)−ϕ)令 ∂ϕ∂ℓ(ϕ,μ0,μ1,Σ)=0⇒ϕ=m∑i=1my(i)=m1i=1∑m1{y(i)=1}
logistic回归中
ℓ ( θ ) = log ∏ i = 1 m p ( y ( i ) ∣ x ( i ) ; θ ) → c o n d i t i o n a l L i k e l i h o o d \ell(\theta) = \log\prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\theta) \rightarrow conditional \ Likelihood ℓ(θ)=logi=1∏mp(y(i)∣x(i);θ)→conditional Likelihood
最大化 ℓ \ell ℓ,得出下面结果:
ϕ = 1 m ∑ i = 1 m 1 { y ( i ) = 1 } μ 0 = ∑ i = 1 m 1 { y ( i ) = 0 } x ( i ) → 标 签 为 0 的 所 有 样 本 x ( i ) 求 和 ∑ i = 1 m 1 { y ( i ) = 0 } → 标 签 为 0 的 样 本 数 目 μ 1 = ∑ i = 1 m 1 { y ( i ) = 1 } x ( i ) ∑ i = 1 m 1 { y ( i ) = 1 } Σ = 1 m ∑ i = 1 m ( x ( i ) − μ y ( i ) ) ( x ( i ) − μ y ( i ) ) T \phi = \frac{1}{m}\sum_{i=1}^{m}1 \lbrace y^{(i)} = 1 \rbrace \\\mu_0 = \frac{{\sum_{i=1}^{m}1 \lbrace y^{(i)} = 0 \rbrace x^{(i)}} \rightarrow 标签为0的所有样本x^{(i)}求和}{{\sum_{i=1}^{m}1 \lbrace y^{(i)} = 0 \rbrace}\rightarrow 标签为0的样本数目} \\\mu_1 = \frac{\sum_{i=1}^{m}1 \lbrace y^{(i)} = 1 \rbrace x^{(i)}}{\sum_{i=1}^{m}1 \lbrace y^{(i)} = 1 \rbrace} \\\Sigma = \frac{1}{m}\sum_{i=1}^{m}(x^{(i)} - \mu_{y^{(i)}})(x^{(i)} - \mu_{y^{(i)}})^T ϕ=m1i=1∑m1{y(i)=1}μ0=∑i=1m1{y(i)=0}→标签为0的样本数目∑i=1m1{y(i)=0}x(i)→标签为0的所有样本x(i)求和μ1=∑i=1m1{y(i)=1}∑i=1m1{y(i)=1}x(i)Σ=m1i=1∑m(x(i)−μy(i))(x(i)−μy(i))T
得到 ϕ , μ 0 , μ 1 , Σ \phi,\mu_0,\mu_1,\Sigma ϕ,μ0,μ1,Σ之后,我们需要预测给定x的情况下最可能的y
arg max y P ( y ∣ x ) = arg max y P ( x ∣ y ) P ( y ) P ( x ) = arg max y P ( x ∣ y ) P ( y ) → P ( x ) 独 立 于 y , 所 以 P ( x ) 值 不 会 变 \mathop{\arg\max}_{y} P(y|x) = \mathop{\arg\max}_{y} \frac{P(x|y)P(y)}{P(x)} \\ = \mathop{\arg\max}_{y} P(x|y)P(y) \rightarrow P(x)独立于y,所以P(x)值不会变 argmaxyP(y∣x)=argmaxyP(x)P(x∣y)P(y)=argmaxyP(x∣y)P(y)→P(x)独立于y,所以P(x)值不会变
arg max y 表 达 式 → 表 达 式 中 最 大 的 y 的 值 m i n ( x − 5 ) 2 = 0 → arg min x ( x − 5 ) 2 = 5 \mathop{\arg\max}_{y}表达式 \rightarrow 表达式中最大的y的值 \\ min(x-5)^2 = 0 \rightarrow\mathop{\arg\min}_{x}(x-5)^2 = 5 argmaxy表达式→表达式中最大的y的值min(x−5)2=0→argminx(x−5)2=5
2 朴素贝叶斯(Naive Bayes)
假定给定y, x i x_i xi是条件独立的:
p ( x 1 , x 2 , … , x 50000 ∣ y ) = p ( x 1 ∣ y ) p ( x 2 ∣ y , x 1 ) p ( x 3 ∣ y , x 1 , x 2 ) … p ( x 50000 ∣ y , x 1 , x 2 , … , x 49999 ) = p ( x 1 ∣ y ) p ( x 2 ∣ y ) p ( x 3 ∣ y ) … p ( x 50000 ∣ y ) = ∏ i = 1 50000 p ( x i ∣ y ) p(x_1,x_2,\dots,x_{50000}|y) = p(x_1|y)p(x_2|y,x_1)p(x_3|y,x_1,x_2)\dots p(x_{50000}|y,x_1,x_2,\dots,x_{49999}) \\ = p(x_1|y)p(x_2|y)p(x_3|y)\dots p(x_{50000}|y) \\ = \prod_{i=1}^{50000}p(x_i|y) p(x1,x2,…,x50000∣y)=p(x1∣y)p(x2∣y,x1)p(x3∣y,x1,x2)…p(x50000∣y,x1,x2,…,x49999)=p(x1∣y)p(x2∣y)p(x3∣y)…p(x50000∣y)=i=1∏50000p(xi∣y)
模型参数:
ϕ j ∣ y = 1 = p ( x j = 1 ∣ y = 1 ) ϕ j ∣ y = 0 = p ( x j = 1 ∣ y = 0 ) ϕ y = p ( y = 1 ) \phi_{j|y=1} = p(x_j = 1|y = 1) \\ \phi_{j|y=0} = p(x_j = 1|y = 0) \\ \phi_{y} = p(y = 1) ϕj∣y=1=p(xj=1∣y=1)ϕj∣y=0=p(xj=1∣y=0)ϕy=p(y=1)
joint likelihood:
ℓ ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = ∏ i = 1 m p ( x i , y i ) \ell(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) = \prod_{i=1}^{m}p(x_i,y_i) ℓ(ϕy,ϕj∣y=0,ϕj∣y=1)=i=1∏mp(xi,yi)
参数推导过程
①、
L ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = ∏ i = 1 m p ( x ( i ) , y ( i ) ) = ∏ i = 1 m { ∏ j = 1 n p ( x j ( i ) ∣ y ( i ) ; ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) } p ( y ( i ) ; ϕ y ) \mathcal{L}(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) = \prod_{i=1}^{m}p(x^{(i)},y^{(i)}) \\ = \prod_{i=1}^{m}\lbrace\prod_{j=1}^{n}p(x_j^{(i)}|y^{(i)};\phi_{j|y=0},\phi_{j|y=1})\rbrace p(y^{(i)};\phi_y) L(ϕy,ϕj∣y=0,ϕj∣y=1)=i=1∏mp(x(i),y(i))=i=1∏m{j=1∏np(xj(i)∣y(i);ϕj∣y=0,ϕj∣y=1)}p(y(i);ϕy)
②、
ℓ ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = log L ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = log ∏ i = 1 m { ∏ j = 1 n p ( x j ( i ) ∣ y ( i ) ; ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) } p ( y ( i ) ; ϕ y ) = ∑ i = 1 m { log ( ∏ j = 1 n p ( x j ( i ) ∣ y ( i ) ; ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) ) + log ( p ( y ( i ) ; ϕ y ) ) } \ell(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) = \log \mathcal{L}(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) \\ = \log\prod_{i=1}^{m}\lbrace \prod_{j=1}^{n}p(x_j^{(i)}|y^{(i)};\phi_{j|y=0},\phi_{j|y=1})\rbrace p(y^{(i)};\phi_y) \\ = \sum_{i=1}^{m} \lbrace \log(\prod_{j=1}^{n}p(x_j^{(i)}|y^{(i)};\phi_{j|y=0},\phi_{j|y=1})) + \log(p(y^{(i)};\phi_y)) \rbrace ℓ(ϕy,ϕj∣y=0,ϕj∣y=1)=logL(ϕy,ϕj∣y=0,ϕj∣y=1)=logi=1∏m{j=1∏np(xj(i)∣y(i);ϕj∣y=0,ϕj∣y=1)}p(y(i);ϕy)=i=1∑m{log(j=1∏np(xj(i)∣y(i);ϕj∣y=0,ϕj∣y=1))+log(p(y(i);ϕy))}
③、
∂ ∂ ϕ y ℓ ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = ∑ i = 1 m ∂ ∂ ϕ y log ( p ( y ( i ) ; ϕ y ) = ∑ i = 1 m ∂ ∂ ϕ y log ( ϕ y 1 { y ( i ) = 1 } ( 1 − ϕ y ) ( 1 − 1 { y ( i ) = 1 } ) = ∑ i = 1 m ∂ ∂ ϕ y { ( 1 { y ( i ) = 1 } log ϕ y ) + ( 1 − 1 { y ( i ) = 1 } ) log ( 1 − ϕ y ) } = ∑ i = 1 m 1 { y ( i ) = 1 } − ϕ y ϕ y ( 1 − ϕ y ) 令 ∂ ∂ ϕ y ℓ ( ϕ y , ϕ j ∣ y = 0 , ϕ j ∣ y = 1 ) = 0 ⇒ ϕ y = ∑ i = 1 m 1 { y ( i ) = 1 } m \left.\frac{\partial}{\partial\phi_y}\right.\ell(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) = \sum_{i=1}^{m}\left.\frac{\partial}{\partial\phi_y}\right.\log(p(y^{(i)};\phi_y) \\ = \sum_{i=1}^{m}\left.\frac{\partial}{\partial\phi_y}\right.\log(\phi_y^{1 \lbrace y^{(i)} = 1 \rbrace}(1 - \phi_y)^{(1 - 1 \lbrace y^{(i)} = 1 \rbrace)} \\ = \sum_{i=1}^{m}\left.\frac{\partial}{\partial\phi_y}\right.\lbrace(1 \lbrace y^{(i)} = 1 \rbrace\log\phi_y) + (1 - 1 \lbrace y^{(i)} = 1 \rbrace)\log(1 - \phi_y)\rbrace \\ = \sum_{i=1}^{m}\frac{1 \lbrace y^{(i)} = 1 \rbrace - \phi_y}{\phi_y(1-\phi_y)} \\ 令 \left.\frac{\partial}{\partial\phi_y}\right.\ell(\phi_y,\phi_{j|y=0},\phi_{j|y=1}) = 0 \Rightarrow \phi_y = \frac{\sum_{i=1}^{m}1 \lbrace y^{(i)} = 1 \rbrace}{m} ∂ϕy∂ℓ(ϕy,ϕj∣y=0,ϕj∣y=1)=i=1∑m∂ϕy∂log(p(y(i);ϕy)=i=1∑m∂ϕy∂log(ϕy1{y(i)=1}(1−ϕy)(1−1{y(i)=1})=i=1∑m∂ϕy∂{(1{y(i)=1}logϕy)+(1−1{y(i)=1})log(1−ϕy)}=i=1∑mϕy(1−ϕy)1{y(i)=1}−ϕy令∂ϕy∂ℓ(ϕy,ϕj∣y=0,ϕj∣y=1)=0⇒ϕy=m∑i=1m1{y(i)=1}
④、

2.1 拉普拉斯平滑(Laplace smoothing)
2.2 文本分类的事件模型(Event models for text classi cation)
多项式事件模型(Multinomial Event Model)
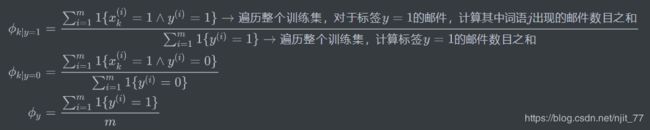
对于第i个训练样本邮件,特征向量 x ( i ) = ( x 1 ( i ) , x 2 ( i ) , … , x n i ( i ) ) , n i = 邮 件 中 词 的 数 量 x^{(i)} = (x_{1}^{(i)},x_{2}^{(i)},\dots,x_{ni}^{(i)}),ni = 邮件中词的数量 x(i)=(x1(i),x2(i),…,xni(i)),ni=邮件中词的数量,特征向量的每个元素 x j = { 1 , 2 , … , 50000 } 字 典 中 的 一 个 索 引 x_j = \lbrace 1,2,\dots,50000 \rbrace字典中的一个索引 xj={1,2,…,50000}字典中的一个索引。
生成模型 p ( x , y ) = { ∏ i = 1 n p ( x i , y ) } p ( y ) p(x,y) = \lbrace \prod_{i=1}^{n}p(x_{i},y) \rbrace p(y) p(x,y)={∏i=1np(xi,y)}p(y)
模型参数
ϕ k ∣ y = 1 = p ( x j = k ∣ y = 1 ) ϕ k ∣ y = 0 = p ( x j = k ∣ y = 0 ) ϕ y = p ( y = 1 ) \phi_{k|y=1} = p(x_j = k|y = 1) \\\phi_{k|y=0} = p(x_j = k|y = 0) \\\phi_{y} = p(y = 1) ϕk∣y=1=p(xj=k∣y=1)ϕk∣y=0=p(xj=k∣y=0)ϕy=p(y=1)
极大似然参数推导过程
①、
L ( ϕ y , ϕ k ∣ y = 0 , ϕ k ∣ y = 1 ) = ∏ i = 1 m p ( x ( i ) , y ( i ) ) = ∏ i = 1 m { ∏ j = 1 n i p ( x j ( i ) ∣ y ( i ) ; ϕ k ∣ y = 0 , ϕ k ∣ y = 1 ) } p ( y ( i ) ; ϕ y ) \mathcal{L}(\phi_y,\phi_{k|y=0},\phi_{k|y=1}) = \prod_{i=1}^{m}p(x^{(i)},y^{(i)}) \\ = \prod_{i=1}^{m}\lbrace\prod_{j=1}^{n_i}p(x_j^{(i)}|y^{(i)};\phi_{k|y=0},\phi_{k|y=1})\rbrace p(y^{(i)};\phi_y) L(ϕy,ϕk∣y=0,ϕk∣y=1)=i=1∏mp(x(i),y(i))=i=1∏m{j=1∏nip(xj(i)∣y(i);ϕk∣y=0,ϕk∣y=1)}p(y(i);ϕy)
②、
ℓ ( ϕ y , ϕ k ∣ y = 0 , ϕ k ∣ y = 1 ) = log L ( ϕ y , ϕ k ∣ y = 0 , ϕ k ∣ y = 1 ) = log ∏ i = 1 m { ∏ j = 1 n i p ( x j ( i ) ∣ y ( i ) ; ϕ k ∣ y = 0 , ϕ k ∣ y = 1 ) } p ( y ( i ) ; ϕ y ) = ∑ i = 1 m { log ( ∏ j = 1 n i p ( x j ( i ) ∣ y ( i ) ; ϕ k ∣ y = 0 , ϕ k ∣ y = 1 ) ) + log ( p ( y ( i ) ; ϕ y ) ) } \ell(\phi_y,\phi_{k|y=0},\phi_{k|y=1}) = \log \mathcal{L}(\phi_y,\phi_{k|y=0},\phi_{k|y=1}) \\ = \log\prod_{i=1}^{m}\lbrace \prod_{j=1}^{n_i}p(x_j^{(i)}|y^{(i)};\phi_{k|y=0},\phi_{k|y=1})\rbrace p(y^{(i)};\phi_y) \\ = \sum_{i=1}^{m} \lbrace \log(\prod_{j=1}^{n_i}p(x_j^{(i)}|y^{(i)};\phi_{k|y=0},\phi_{k|y=1})) + \log(p(y^{(i)};\phi_y)) \rbrace ℓ(ϕy,ϕk∣y=0,ϕk∣y=1)=logL(ϕy,ϕk∣y=0,ϕk∣y=1)=logi=1∏m{j=1∏nip(xj(i)∣y(i);ϕk∣y=0,ϕk∣y=1)}p(y(i);ϕy)=i=1∑m{log(j=1∏nip(xj(i)∣y(i);ϕk∣y=0,ϕk∣y=1))+log(p(y(i);ϕy))}
③、
∂ ∂ ϕ y ℓ ( ϕ y , ϕ k ∣ y = 0 , ϕ k ∣ y = 1 ) = ∑ i = 1 m ∂ ∂ ϕ y log ( p ( y ( i ) ; ϕ y ) = ∑ i = 1 m ∂ ∂ ϕ y log ( ϕ y 1 { y ( i ) = 1 } ( 1 − ϕ y ) ( 1 − 1 { y ( i ) = 1 } ) = ∑ i = 1 m ∂ ∂ ϕ y { ( 1 { y ( i ) = 1 } log ϕ y ) + ( 1 − 1 { y ( i ) = 1 } ) log ( 1 − ϕ y ) } = ∑ i = 1 m 1 { y ( i ) = 1 } − ϕ y ϕ y ( 1 − ϕ y ) 令 ∂ ∂ ϕ y ℓ ( ϕ y , ϕ i ∣ y = 0 , ϕ i ∣ y = 1 ) = 0 ⇒ ϕ y = ∑ i = 1 m 1 { y ( i ) = 1 } m \left.\frac{\partial}{\partial\phi_y}\right.\ell(\phi_y,\phi_{k|y=0},\phi_{k|y=1}) = \sum_{i=1}^{m}\left.\frac{\partial}{\partial\phi_y}\right.\log(p(y^{(i)};\phi_y) \\ = \sum_{i=1}^{m}\left.\frac{\partial}{\partial\phi_y}\right.\log(\phi_y^{1 \lbrace y^{(i)} = 1 \rbrace}(1 - \phi_y)^{(1 - 1 \lbrace y^{(i)} = 1 \rbrace)} \\ = \sum_{i=1}^{m}\left.\frac{\partial}{\partial\phi_y}\right.\lbrace(1 \lbrace y^{(i)} = 1 \rbrace\log\phi_y) + (1 - 1 \lbrace y^{(i)} = 1 \rbrace)\log(1 - \phi_y)\rbrace \\ = \sum_{i=1}^{m}\frac{1 \lbrace y^{(i)} = 1 \rbrace - \phi_y}{\phi_y(1-\phi_y)} \\ 令 \left.\frac{\partial}{\partial\phi_y}\right.\ell(\phi_y,\phi_{i|y=0},\phi_{i|y=1}) = 0 \Rightarrow \phi_y = \frac{\sum_{i=1}^{m}1 \lbrace y^{(i)} = 1 \rbrace}{m} ∂ϕy∂ℓ(ϕy,ϕk∣y=0,ϕk∣y=1)=i=1∑m∂ϕy∂log(p(y(i);ϕy)=i=1∑m∂ϕy∂log(ϕy1{y(i)=1}(1−ϕy)(1−1{y(i)=1})=i=1∑m∂ϕy∂{(1{y(i)=1}logϕy)+(1−1{y(i)=1})log(1−ϕy)}=i=1∑mϕy(1−ϕy)1{y(i)=1}−ϕy令∂ϕy∂ℓ(ϕy,ϕi∣y=0,ϕi∣y=1)=0⇒ϕy=m∑i=1m1{y(i)=1}
④、