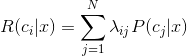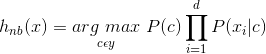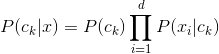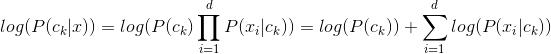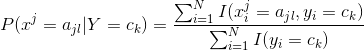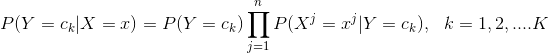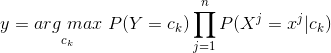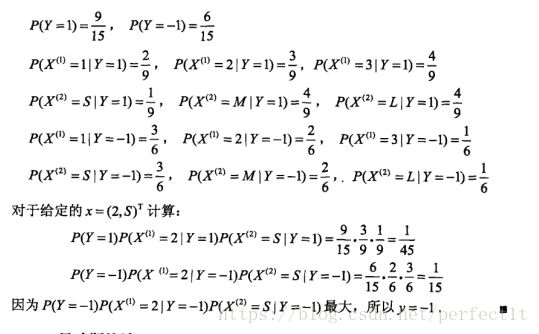机器学习之朴素贝叶斯(Naive Bayes)

贝叶斯概率以18世纪的一位神学家托马斯·贝叶斯(Thomas Bayes)的名字命名。

一、为什么叫朴素贝叶斯？

朴素贝叶斯是经典机器学习算法之一，是基于概率论的分类算法，其原理简单，易于实现，多使用于文本分类，如垃圾邮件过滤、新闻分类等。

朴素贝叶斯中的朴素是来源于该算法是基于属性条件独立性假设，即对于已知类别，假设所有属性(特征)相互独立；而贝叶斯则是其基于贝叶斯定理而得到的。

所以说朴素贝叶斯算法就是基于"属性条件独立"和“贝叶斯定理”推导得到的算法。

二、算法原理

1、贝叶斯决策论

在讲解原理之前，我们先来认识一下贝叶斯决策论，贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法。对分类任务来说，在所有相关概率都已知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。

有N种可能的类别标记，即，是将标记为判定为所产生的损失。基于后验概率可获得将样本x分类为所产生的期望损失(expected loss)，即在样本x上的“条件风险”(conditional risk):

                                   

贝叶斯判定准则(Bayes decision rule): 为最小化总体的风险，只需在每个样本上选择那个能使条件风险最小的类别标记，即

                                    

此时， 称为贝叶斯最优分类器。

具体来说，若目标是最小化分类错误率，则误判损失可以写为 

                                     。

那么此时的条件风险为：

                                   

注：由得，当样本x原来为c类，所以条件风险为。

于是，最小化分类错误率的贝叶斯最优分类器为：

                                    

也就是说，对每个样本x，选择能使后验概率P(c|x)最大的类别标记。

不难看出，如果想使用贝叶斯判定准则来最小化决策风险，则需要先得到后验概率P(c|x)。后验概率的获得主要有两种策略：

1. 判别式模型：给定x，通过直接建模P(c|x)来预测c。
2. 生成式模型：先对联合概率分布P(x,c)进行建模，然后在获得P(c|x)。

下面，我们来讲生成式模型：

                                                

由贝叶斯定理，P(c|x)可写为：

                                                

其中，P(c)是先验概率；P(x|c)是样本x相对于类标记c的类条件概率，或称为“似然”；P(x)是用于归一化的证据因子，在给定x的情况，P(x)与属于哪个类无关，所以估计P(c|x)的问题就被转换为如何基于训练数据D来估计先验概率P(c)和似然P(x|c)。

2、极大似然估计

对于这个函数：P(x|θ)
输入有两个：x表示某一个具体的数据；θ表示模型的参数。

1. 如果θ是已知确定的，x是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。
2. 如果x是已知确定的，θ是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数θ，出现x这个样本点的概率是多少。

极大似然估计方法（Maximum Likelihood Estimate，MLE）也称为最大概似估计或最大似然估计，是求估计的另一种方法。它是建立在极大似然原理的基础上的一个统计方法。也就是在参数θ的可能取值范围内，选取使L(θ)达到最大的参数值θ，作为参数θ的估计值。

3、朴素贝叶斯

朴素贝叶斯是贝叶斯决策论的一部分，其假设“属性间条件独立”，也就是说，对于已知的类别，假设所有的属性相互独立。从前面贝叶斯决策论，我们知道：

                                                

也就是估计P(c|x)的问题就被转换为如何基于训练数据D来估计先验概率P(c)和似然(类条件概率)P(x|c)。P(x|c)是所有属性上的联合概率，难以从有限的训练样本直接估计而得，而朴素贝叶斯的属性条件独立假设则避开了该障碍。

基于属性间条件独立假设，对上式可以重写为：

                                               

其中d为属性数目，为在第i个属性上的取值。

又由于对于给定的x，其对所有的类别来说P(x)都是相同的，所以基于风险(损失)最小化准则得到后验概率最大化准则可以写为：

                                               

这就是朴素贝叶斯分类器的表达式，即对于给定的样本x，我们计算每个类别的后验概率：

                                              

而其中得到的后验概率最大的类别作为分类的结果。这就是朴素贝叶斯算法采用的原理，即根据期望风险最小化准则得到的后验概率最大化准则。

在实际工作应用中，为防止连乘产生数值下溢，后验概率的计算，通常采用对数进行转换，即：

                 

三、参数估计

1、采用极大似然估计

在前面的知识，我们知道，学习意味着估计和，这里表示第j个属性上的取值。那么可以应用极大似然估计法估计相应的概率。先验概率的极大似然估计为：

                                             

设第j个特征可能的取值为，则条件概率的极大似然估计为：

                                            

                                            

其中，表示第i个样本的第j个特征；是第j个特征可能取值的第l个值；I为指数函数。

直观的解释就是：令表示训练集D中第c类样本组成的集合，则先验概率为

                                            

其中，表示类别为c的总个数，表示样本总数，也就是说先验概率等于类别为c的样本数比上总样本数。

令表示中在第i个属性上取值为的样本组成的集合，则条件概率为：

                                           

也就是说，条件概率等于类别为c且在第i个属性取值为的样本个数比上类别为c的样本个数。

以上是对于离散属性的情况，那么对于连续情况呢？对于连续情况，可考虑概率密度函数，假定

                                           

其中和 分别是第c类样本在第i个属性上取值的均值和方差，则有：

                                           

 2、学习与分类算法

输入：训练数据，其中，表示第i个样本的第j个属性(特征)，，是第j个特征可能取的第l个值，;  实例x。

输出：实例x的分类。

(1) 计算先验概率及条件概率

                                         

                                         

                                          

(2) 对于给定的实例，计算

                       

(3) 确定实例x的类

                       

例子：

3、拉普拉斯修正(平滑)

用极大似然估计可能会出现所要估计的概率值为0的情况。若使用极大似然估计，则会影响后验概率的结果，即在连乘处直接会使结果为0，是分类产生偏差。解决该问题，常用贝叶斯估计，而拉普拉斯平滑是贝叶斯估计的一种，也是最常用的一种。

具体来说，令N表示训练集D中可能的类别数，表示第i个属性可能的取值数，则

                                      

                                      

其他不变。

四、python实现与实践

代码和数据--------GitHub：https://github.com/davidHdw/machine-learning

1、简单文本分类

# -*- coding: utf-8 -*-

# Bayes.py

import numpy as np

def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help','please'],
                   ['maybe', 'not', 'take', 'him', 'to','dog','park','stupid'],
                   ['my', 'dalmation', 'is','so','cute', 'I', 'love','him'],
                   ['stop', 'posting', 'stupid','worthless', 'garbage'],
                   ['mr', 'licks','ate','my','steak', 'how', 'to','stop','him'],
                   ['quit','buying','worthless','dog','food','stupid']]
    classVec = [0,1,0,1,0,1]
    return postingList, classVec
    
def createVocabList(dataSet):
    '''
    函数说明：将实验样本处理成词汇表
    输入：
        dataSet : 整理的样本数据集
    返回：
        vocabSet : 词汇表
    '''
    vocabSet = set([])
    for document in dataSet:
        vocabSet = vocabSet | set(document)
    return list(vocabSet)

def setOfWords2Vec(vocabList, inputSet):
    '''
    函数说明：根据vocabList词汇表，将inputSet向量化，向量的元素为1或0
    输入：
        vocabList：createVocabList返回的词汇表
        inputSet：切分的词条列表
    返回：
        returnVec : 文档向量，词集模型
    '''
    returnVec = [0] * len(vocabList)    # 创建一个所有元素都为0的向量
    for word in inputSet:               # 遍历每个词条
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1    # 词存在词汇表中，则置1
        else :
            print("The word: %s is not in my Vocabulary!" % word)
    return returnVec

def bagOfWord2VecMN(vocabList, inputSet):
    '''
    函数说明：根据vocabList词汇表，将inputSet向量化，向量的元素对应词出现的次数
    词袋模式：
    输入：
        vocabList：createVocabList返回的词汇表
        inputSet：切分的词条列表
    返回：
        returnVec : 文档向量，词集模型
    '''
    returnVec = [0] * len(vocabList)    # 创建一个所有元素都为0的向量
    for word in inputSet:               # 遍历每个词条
        if word in vocabList:
            returnVec[vocabList.index(word)] += 1    # 词存在词汇表中，则出现次数自加1
    return returnVec 

def trainNB0(trainMatrix, trainCategory):
    '''
    函数说明：朴素贝叶斯分类器训练函数
    输入：
        trainMatrix：训练文档矩阵，即setOfWords2Vec返回的returnVec构成的矩阵
        trainCategory：训练类别标签向量，即loadDataSet返回的classVec
    返回：
        p0Vect： 非的条件概率数组, P(x_i|c=0) 
        p1Vect： 侮辱类的条件概率数组, P(x_i|c=1)
        pAbusive：文档属于侮辱类的概率，即P(C=1),而P(C=0)=1-P(c=1)
    '''
    numTrainDocs = len(trainMatrix) # 文章数目
    numWords = len(trainMatrix[0])  # 文章长度，因经过setOfWords2Vec处理，所以都一样长
    pAbusive = sum(trainCategory) / float(numTrainDocs) # 类别为1的先验概率P(c=1)
    # 创建一个长度为numWords且值全为0的数组p0Num，
    # 用于统计在类别为0的训练样本中各个属性(此处为词)的出现的次数
    p0Num = np.zeros(numWords) 
    p1Num = np.zeros(numWords)
    p0Demo = 0.0
    p1Demo = 0.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            # 出现的词自加1
            p1Num += trainMatrix[i]
            # 该类别的总词数加上当前样本的词数
            p1Demo += sum(trainMatrix[i])
        else :
            p0Num += trainMatrix[i]
            p0Demo += sum(trainMatrix[i])
    p1Vect = p1Num/p1Demo # 每个元素除以该类别中的总词数
    p0Vect = p0Num/p0Demo
    return p0Vect, p1Vect, pAbusive
    
def trainNB1(trainMatrix, trainCategory):
    '''
    函数说明：朴素贝叶斯分类器训练函数,为防止出现概率为0导致，分类出现偏差，采用“拉普拉斯平滑”
             又为防止连乘出现数值下溢，对结果进行取对数
    输入：
        trainMatrix：训练文档矩阵，即setOfWords2Vec返回的returnVec构成的矩阵
        trainCategory：训练类别标签向量，即loadDataSet返回的classVec
    返回：
        p0Vect： 非的条件概率数组, P(x_i|c=0) 
        p1Vect： 侮辱类的条件概率数组, P(x_i|c=1)
        pAbusive：文档属于侮辱类的概率，即P(C=1),而P(C=0)=1-P(c=1)
    '''
    numTrainDocs = len(trainMatrix) # 文章数目
    numWords = len(trainMatrix[0])  # 文章长度，因经过setOfWords2Vec处理，所以都一样长
    pAbusive = (sum(trainCategory)+1) / float(numTrainDocs+2) # 类别为1的先验概率P(c=1)
    # 创建一个长度为numWords且值全为1的数组p0Num，(参考拉普拉斯修正)
    # 用于统计在类别为0的训练样本中各个属性(此处为词)的出现的次数
    p0Num = np.ones(numWords) 
    p1Num = np.ones(numWords)
    p0Demo = 2.0  # 每个词(属性)只会出现为0,1;所以初始为2.0
    p1Demo = 2.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            # 出现的词自加1
            p1Num += trainMatrix[i]
            # 该类别的总词数加上当前样本的词数
            p1Demo += sum(trainMatrix[i])
        else :
            p0Num += trainMatrix[i]
            p0Demo += sum(trainMatrix[i])
    p1Vect = p1Num/p1Demo # 每个元素除以该类别中的总词数
    p0Vect = p0Num/p0Demo
    return np.log(p0Vect), np.log(p1Vect), pAbusive

def classifyNB(vec2Classify, p0Vect, p1Vect, pClass1):
    '''
    函数说明：朴素贝叶斯分类器分类函数
    参数：
        vec2Classify：待分类的词条数组
        p0Vect：非侮辱类的条件概率数组
        p1Vect：侮辱类的条件概率数组
        pClass1 ： 侮辱类的先验概率
    返回：
        1 : 侮辱类
        0 ：非侮辱类
    '''
    p1 = sum(p1Vect * vec2Classify) + np.log(pClass1)
    p0 = sum(p0Vect * vec2Classify) + np.log(1 - pClass1)
    if p1 > p0 :
        return 1
    else:
        return 0
    
def testingNB():
    '''
    函数说明:测试朴素贝叶斯分类器
    '''
    listOPosts, listClass = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    print(myVocabList)
    print(setOfWords2Vec(myVocabList, listOPosts[0]))
    trainMat = []
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0v, p1v, pAb = trainNB1(trainMat, listClass)    
    testEntry = ['love', 'my','dalmation']
    thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry, 'classifyed as: ','侮辱类' if classifyNB(thisDoc, p0v, p1v, pAb) else '非侮辱类')
    testEntry = ['stupid', 'garbage']
    thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry, 'classifyed as: ','侮辱类' if classifyNB(thisDoc, p0v, p1v, pAb) else '非侮辱类')    
    
if __name__ == "__main__":
    testingNB()
    

上面的代码只是简单的对词集模式进行测试，有兴趣可以自己测试词袋模式且进行更深入的使用与学习。

2、使用上面的朴素贝叶斯过滤垃圾邮件

# -*- coding: utf-8 -*-

# Bayes-spam.py

import numpy as np
import Bayes

def textParse(bigString):
    '''
    函数说明：
    
    '''
    import re
    listOpTokens = re.split(r'\W*', bigString)
    return [tok.lower() for tok in listOpTokens if len(tok) > 2]

def spamTest():
    '''
    '''
    docList = []
    classList = []
    fullText = []
    for i in range(1, 26):
        wordList = textParse(open('email/spam/%d.txt' % i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)
        wordList = textParse(open('email/ham/%d.txt' % i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
    vocabList = Bayes.createVocabList(docList)
    trainingSet = list(range(50))
    testSet = []
    for i in range(10):
        randIndex = int(np.random.uniform(0, len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del(trainingSet[randIndex])
    trainMat = []
    trainClasses = []
    for docIndex in trainingSet:
        trainMat.append(Bayes.setOfWords2Vec(vocabList, docList[docIndex]))
        trainClasses.append(classList[docIndex])
    p0v, p1v, pSpam = Bayes.trainNB1(np.array(trainMat), np.array(trainClasses))
    errorCount = 0
    for docIndex in testSet:
        wordVector = Bayes.setOfWords2Vec(vocabList, docList[docIndex])
        if Bayes.classifyNB(np.array(wordVector), p0v, p1v, pSpam) \
        != classList[docIndex]:
            errorCount += 1
    print("the error rate is: ", float(errorCount/len(testSet)))
    
if __name__ == '__main__':
    spamTest()

五、总结

朴素贝叶斯算法是基于贝叶斯准则和属性条件独立的一种算法，通常应用与文本分类任务。其根据期望风险最小化准则得到后验概率最大准则，即要使分类结果最靠谱最准确，则其期望损失需要最小，即只要后验概率最大那么其期望损失就会最小。由贝叶斯准则，后验概率可以通过如下方法得到：

                                                     

又朴素贝叶斯假设属性条件独立，所以有：

                                                                

通常，我们采用极大似然估计法，来对其参数进行估计，但极大似然估计会遇到概率为0的情况，会出现分类偏差，为解决该问题，一般采用拉普拉斯修正对极大似然估计进行改正。

朴素贝叶斯分类器的表达式为：

                                                   

即选择后验概率最大的类别作为分类的结果。

六、参考

1、《机器学习》 周志华 ---- 西瓜书

2、《统计学习方法》李航

3、《机器学习实战》李锐  译