leetcode周赛 （2020/06/15）

1. 一位数组的动态和

class Solution {
public:
    vector<int> runningSum(vector<int>& nums) {
        vector<int> sum;
        int N = nums.size();
        sum.resize(N);
        sum[0] = nums[0];
        for(int i=1;i<N;i++)
        {
            sum[i] = sum[i-1]+nums[i];
            //tot+= sum[i];
        }
        return sum;
        
    }
};

2. 不同整数的最少数目

struct Node
{
    int val;
    int cnt;
    bool operator < (Node b)
    {
        return cnt < b.cnt;
    }
};
class Solution {
public:
    int findLeastNumOfUniqueInts(vector<int>& arr, int k) {
        vector<Node> node;
        unordered_map<int,int> pos;
        node.resize(arr.size());
        int t = 0;
        for(int x:arr)
        {
            if(pos.find(x)==pos.end())
            {
                pos[x] = t++;
                node[pos[x]].val = x;
                node[pos[x]].cnt = 1;
            }
            else{
                int p = pos[x];
                node[p].cnt++;
            }
        }
        int ind = 0;
        int N = t;
        int dec = 0;
        sort(node.begin(),node.begin()+t);
        while(ind<t&&k>0)
        {
            if(node[ind].cnt<=k)
            {
                k-=node[ind].cnt;
                dec++;
            }
            else{
                k = 0;
            }
            ind++;
        }
        return N-dec;
    }
};

3.制作m束花所需的最少天数

思路1 二分法

二分法的解法很简单，但是比赛的时候没想到。。。

bool check(vector<int>& bloomyDay, int m, int k, int mid)
{
    int tmp = 0;
    for(int x:bloomyDay)
    {
        if(x<=mid)
            tmp++;
        else
            tmp=0;
        if(tmp>=k)
        {
            tmp-=k;
            m--;
        }
    }
    return m<=0;
}
class Solution {
public:

    int minDays(vector<int>& bloomDay, int m, int k) {
        int N = bloomDay.size();
        if(m*k>N)
            return -1;
        int le = 0;
        int ri = 1e9+1;
        int mid = (ri-le)/2+le;
        bool flag =false;
        while(le<ri)
        {
            mid = (ri-le)/2+le;
            if(check(bloomDay, m, k, mid)){
                ri = mid;
                flag =true;
            }
            else{
                le = mid+1;
            }
        }
        if(!flag)
            return -1;
        return le;
    }
};

思路2 区间维护

用两个数组l,r，l[i]表示l[i] ~ i连续盛开，r[i]表示i ~ r[i]连续盛开
比赛的时候就是这思路，但是不够清晰明白，没有调出来，强推B站大雪菜，讲解非常清晰。

#include 
#include 
#include 
using namespace std;
class Solution {
public:
    //从l到r花束的数目
    int get(int l,int r, int k)
    {
        return (r - l + 1) / k;
    }
    int minDays(vector<int>& bloomDay, int m, int k) {
        //x.first表示盛开的日子，x.second表示下标
        vector<pair<int,int> > vec;
        int N = bloomDay.size();
        for(int i=0;i<bloomDay.size();i++)
            vec.push_back({bloomDay[i],i+1});
        //l[i]表示从i到l[i]连续盛开
        //r[i]表示从i到r[i]连续盛开
        vector<int> l(N+2), r(N+2);
        sort(vec.begin(),vec.end());
        int sum = 0;
        for(auto x : vec)
        {
            int i = x.second;
            //如果左端有盛开的花&&右端有盛开的花
            if(l[i-1] && r[i+1])
            {
                sum = sum + get(l[i-1], r[i+1], k)- get(l[i-1],i-1,k) - get(i+1, r[i+1], k);
                r[l[i-1]] = r[i+1];
                l[r[i+1]] = l[i-1];
            }
            //如果只有左端有盛开的花
            else if(l[i-1])
            {
                sum = sum + get(l[i-1],i,k) - get(l[i-1],i-1,k) ;
                r[l[i-1]] = i;
                l[i] = l[i - 1];
            }
            //如果只有右端有盛开的花
            else if(r[i+1]){
                sum = sum + get(i,r[i+1],k) - get(i+1,r[i+1],k);
                r[i] = r[i+1];
                l[r[i+1]] = i;
            }
            //如果都没有花
            else{
                sum = sum + get(i,i,k);
                r[i] = l[i] = i;
            }
            if(sum>=m)
            {
                return x.first;
            }
        }
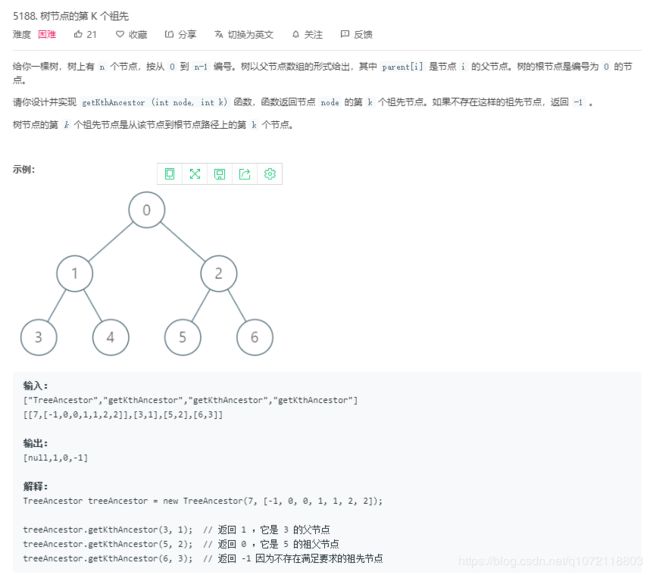
        return -1;
    }
};

4. 树节点的第k个祖先

代码

LCA倍增
f[node][k]表示node的第 2^k个祖先节点
f[node][k] = f[f[[node][k-1]][k-1]

class TreeAncestor {
private:
    vector<vector<int>> f;
    vector<vector<int>> children;
public:
    TreeAncestor(int n, vector<int>& parent) {
        f = vector<vector<int>>(n,vector<int>(16,-1));
        children.resize(n);
        int root = 0;
        for(int i=0;i<parent.size();i++)
        {
            if(parent[i]==-1)
            {
                root = i;
                continue;
            }
            children[parent[i]].push_back(i);
        }
        queue<int> que;
        que.push(root);
        while(que.size())
        {
            int ne = que.front();
            que.pop();
            for(int child : children[ne])
            {
                f[child][0] = parent[child];
                for(int k=1;k<16;k++)
                {
                    if(f[child][k-1]<0)
                        break;
                    f[child][k] = f[f[child][k-1]][k-1];
                }
                que.push(child);   
            }
            
        }
    }
    
    int getKthAncestor(int node, int k) {
        for(int i=0;i<16;i++)
        {
            if(k>>i&1)
            {
                node = f[node][i];
                if(node==-1)
                    return node;
            }
        }
         return node;
    }
};

/**
 * Your TreeAncestor object will be instantiated and called as such:
 * TreeAncestor* obj = new TreeAncestor(n, parent);
 * int param_1 = obj->getKthAncestor(node,k);
 */