ML:最近邻算法
最近邻算法
一、算法概述
最近邻算法或者说KNN算法,是一种基本的分类与回归方法,是数据挖掘技术中最简单的技术之一。Cover和Hart在1968年提出了最初的邻近算法,它的输入是基于实例的学习(instance-based learning),属于懒惰学习(lazy learning)即KNN是一种非显示学习过程,也就是没有训练阶段,对新样本直接与训练集做分类或者回归预测。
所谓最近邻,就是首先选取一个阈值为K,对在阈值范围内离测试样本最近的点进行投票,票数多的类别就是这个测试样本的类别,这是分类问题。那么回归问题也同理,对在阈值范围内离测试样本最近的点取均值,那么这个值就是这个样本点的预测值。
二、学习过程
1、分类
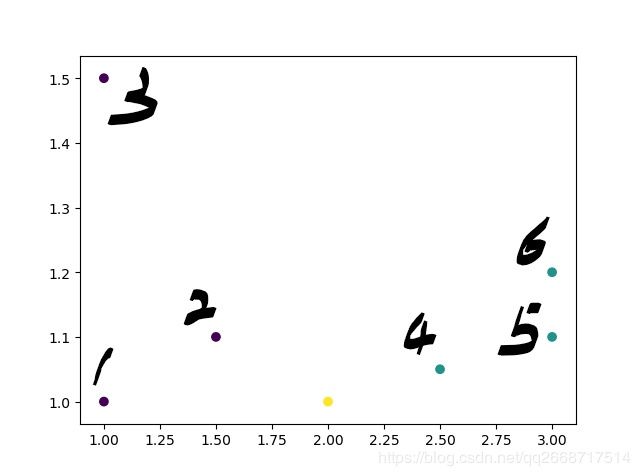
先举个简单的例子,如下图数据:
假设紫色的点是类“1”,绿色的点是类“0”,而黄色的点是我们要预测的样本点。在这里我们采用欧式距离为我们的衡量标准。
1点与样本点的距离为: ( 2.0 − 1.0 ) 2 + ( 1.0 − 1.0 ) 2 = 1 \sqrt{(2.0 - 1.0)^2+(1.0-1.0)^2}=1 (2.0−1.0)2+(1.0−1.0)2=1
2点与样本点的距离为: ( 2.0 − 1.5 ) 2 + ( 1.0 − 1.1 ) 2 = 0.510 \sqrt{(2.0-1.5)^2+(1.0-1.1)^2}=0.510 (2.0−1.5)2+(1.0−1.1)2=0.510
3点与样本点的距离为: ( 2.0 − 1.0 ) 2 + ( 1.0 − 1.5 ) 2 = 1.118 \sqrt{(2.0-1.0)^2+(1.0-1.5)^2}=1.118 (2.0−1.0)2+(1.0−1.5)2=1.118
4点与样本点的距离为: ( 2.5 − 2.0 ) 2 + ( 1.05 − 1.0 ) 2 = 0.502 \sqrt{(2.5-2.0)^2+(1.05-1.0)^2}=0.502 (2.5−2.0)2+(1.05−1.0)2=0.502
5点与样本点的距离为: ( 3.0 − 2.0 ) 2 + ( 1.1 − 1.0 ) 2 = 1.004 \sqrt{(3.0-2.0)^2+(1.1-1.0)^2}=1.004 (3.0−2.0)2+(1.1−1.0)2=1.004
6点与样本点的距离为: ( 3.0 − 2.0 ) 2 + ( 1.2 − 1.0 ) 2 = 1.020 \sqrt{(3.0-2.0)^2+(1.2-1.0)^2}=1.020 (3.0−2.0)2+(1.2−1.0)2=1.020
令K=3时,距离样本点最近的三个点为1,2,4对应的类别为“1”,“1”,“0”,所以此时样本点为“1”类别。
令K=4时,距离样本点最近的四个点对应的类别为“1”,“1”,“0”,“0”,此时重新选取K值计算。
令K=5时,距离样本点最近的五个点对应的类别为“1”,“1”,“0”,“0”,“0”,所以此时样本点为“0”类别。
2、回归
与分类问题大同小异,在训练数据中选取与样本点相似特征的K个点并取均值,即为样本点的预测值。
举个简单的例子:
| 总房间数 | 卧室数量 | 价格 |
|---|---|---|
| 7 | 2 | 100 |
| 7 | 3 | 150 |
| 9 | 2 | 300 |
假设我有一个2卧室的房子,如果K=2,根据数据我可以得到我房子的价格为 ( 100 + 300 ) / 2 = 200 (100+300)/2=200 (100+300)/2=200
三、总结
最近邻算法使用的模型实际上对应于特征空间的划分。模型由三个基本要素组成:距离度量、K值、分类决策规则。
K值的选取:
如果选择较小的K值,就相当于用较小的领域中的训练实例进行预测,“学习”的近似误差会减小,只有与输入实例较近的训练实例才会对预测结果起作用。但缺点是“学习”的误差估计会增大,预测结果会对近邻的实例点非常敏感,如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,K值得减小就意味着整体模型变得复杂,易发生过拟合。
如果选择较大的K值,就相当于用较大领域中的训练实例进行预测。优点是可以减少学习的估计误差,但缺点是近似误差会增大。这时与输入实例较远的训练实例也会对预测起作用,使预测发生误差。K值增大会使模型变得简单。
在应用中,K值一般选取一个比较小的数值。通常采用交叉验证法来选取最优的K值。
最近邻算法的优点:思想简单,可用与分类与回归,准确度高,对噪声不敏感。
缺点:计算量大,难解决样本不平衡问题,需要大量内存。
代码:
import numpy as np
import matplotlib.pyplot as plt
import operator
# 设置数据
x_data = np.array([[3, 104], [2, 100], [1, 81], [101, 10], [99, 5], [98, 2]])
y_data = np.array(["R", "R", "R", "A", "A", "A"])
# 设置位置测试数据
x_test = np.array([[18, 90]])
# 数据的行数
x_size = x_data.shape[0]
x_test = np.tile(x_test, (x_size, 1))
# print(x_test)
# 计算欧式距离
Eur_dis = np.square(x_data - x_test).sum(axis=1) ** 0.5
# print(Eur_dis)
# 排序
sortArg = Eur_dis.argsort()
# print(sortArg)
k = 5
classCount = {}
for i in range(k):
votelabel = y_data[sortArg[i]]
classCount[votelabel] = classCount.get(votelabel, 0) + 1
# print(classCount)
# 对字典的值进行排序
# classCount.item()将字典的键和值分为两个部分
# key = operator.itemgetter(1)表示对值进行排序,如果是0,表示对键进行排序
# reverse表降序
sortArgClass = sorted(classCount.items(), key=operator.itemgetter(0), reverse=True)
print(sortArgClass)
# 获取数量最多的标签
knnclass = sortArgClass[0][0]
print(knnclass)